die Binomialverteilung

Bei den klassischen (Skat-)Kartenspielen werden

Also sind

Es gibt also

Gegeben sei folgendes Experiment:

  1. wird aus einem Satz klassischer Spielkarten zwei Mal nacheinander jeweils eine Karte gezogen;
  2. wird die beim ersten Mal gezogene Karte direkt danach (also vor dem zweiten Ziehen) wieder in den Stapel zurück gelegt, so dass

(d.h. nicht "bedingt")

sind,

(hier wird schon klar, dass es völlig uninteressant ist, wie viele Karten im Stapel sind

[beim klassischen Skatspiel sind es acht  von jeder "Farbe", also insgesamt 4 • 8 = 32 Karten),

sondern Hauptsache, alle vier "Farben"  , ,und kommen gleich oft bzw.  jeweils zu vor);

  1. schränken wir unsere Perspektive schon massiv ein:
  1. Einschränkung:

  • uns interessiert nicht die Einzelkarte

(also z.B. oder oder ),

  • sondern uns interessieren nur die "Farben" , ,und

(also interessiert z.B. an nicht, dass ein Ass, sondern nur, dass vorliegt).

Man könnte also genauso gut den Kartenstapel aus Karten zusammensetzen, auf denen nur die "Farben" , ,und zu sehen wären:

Nebenbei: solchen Einschränkungen sind ja eben ein Grundzug der Wahrscheinlichkeitsrechnung, den wir unten noch weiter verschärfen werden: es interessieren

(z.B. ),

(z.B. alle - Karten bzw. eine beliebige - Karte, aber egal welche),

(Median, Erwartungswert) 

D.h. wir wollen nicht mehr alle (evtl. unüberschaubar viele) Einzelereignisse betrachten, sondern ganz schnell

(z.B. wenn wir unten alle Binomialverteilungen mit gleichem p, aber unterschiedlichen n vergleichen;

oder ein anderes Beispiel: wenn zwei Mathearbeiten

[die allerdings keine Wahrscheinlichkeitsverteilungen sind, nämlich hoffentlich nicht vom Lehrer ausgewürfelt wurden]

in zwei verschieden großen Klassen geschrieben wurden, ist beispielsweise die absolute Anzahl der Einsen wenig aussagekräftig, sondern hilft schon eher der Vergleich der Durchschnitte = Mittelwerte).

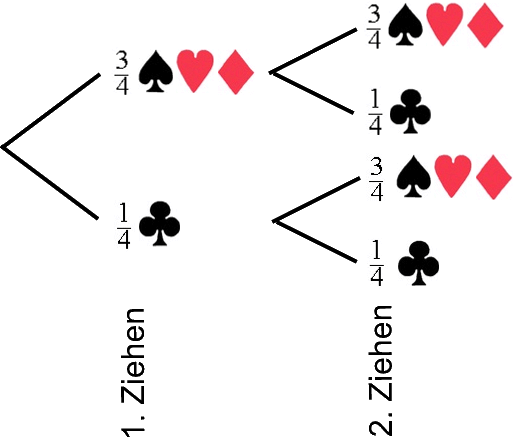
Eine erste Veranschaulichung von Zufallsexperimenten bieten Baumdiagramme. Bei unserer oben gestellten Aufgabe sieht das Baumdiagramm so aus:

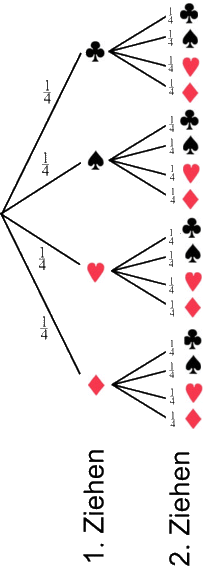
Bei jedem Ziehen erscheint dabei jede "Farbe" , ,und mit der Wahrscheinlichkeit  .

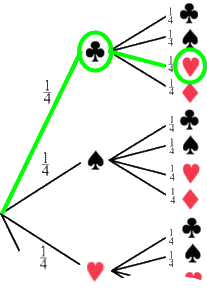
So lässt sich nun die Wahrscheinlichkeit vieler Doppelziehungen berechnen, also z.B.

, 

und deshalb ergibt sich die Wahrscheinlichkeit für und (in genau dieser Reihenfolge!) als • = ;

 .

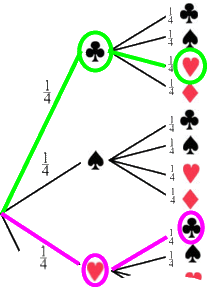Für jeden der beiden Wege ergibt sich jeweils die Wahrscheinlichkeit , für beide zusammen also die Wahrscheinlichkeit + = .

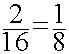Nun hat der Baum

aber bereits nach nur zweimaligem Ziehen arg viele Zweige

(   

und wird somit schnell sehr groß und unübersichtlich.

Deshalb kommen wir zur

2. Einschränkung

Uns interessiert nur noch, wie oft gezogen wird, und alle anderen Fälle ,und fassen wir zu "Nicht-" zusammen.

Es gibt also nur noch die zwei Fälle:
  1.           ,
  2. Nicht-  (zusammengesetzt aus  ,und ).

Dabei erscheint

Im Grunde interessiert uns also nur das Ereignis , während alles andere ( ,und ) nur "der billige Rest" ist bzw. das, was Fischer unnötigen und mühsamen "Beifang" nennen.

Z.B. ist   in einem Kartenspiel von besonderem Interesse, wenn der vorherige Spieler etwa ein - Ass gelegt hat und ich nun "bedienen" muss, aber weder eine - Karte noch ein Ass habe, also eine Karte vom zentralen Stapel "ziehen" muss. Dann interessieren mich nicht im mindesten ,und (die ich ja eventuell schon auf der Hand habe), sondern nur (oder ein Ass).

Ein anderes schönes Beispiel ist : da erscheint zwar die 6 mit derselben Wahrscheinlichkeit (nämlich ) wie die anderen Zahlen  1, 2, 3, 4 und 5 , aber die 6 hat doch eine ganz andere, sogar doppelte Bedeutung:  

  1. kann ich nur mit ihr aus meiner Ecke raus,
  2. darf ich, wenn sie fällt, nochmal würfeln.

Wenn ich also beispielsweise noch keine einzige Figur aus meiner Ecke heraus bekommen habe, interessiert am nächsten Wurf überhaupt nur eine 6, während alle anderen Zahlen 1, 2, 3, 4 und 5 "Restmüll" sind. Da ist es dann auch völlig uninteressant, welche der Zahlen 1, 2, 3, 4 oder 5 fällt, sondern es ist nur ärgerlich, wenn keine 6 fällt.

Halten wir aber zwischendurch kurz fest:

Wir betrachten ab sofort nur noch Wahrscheinlichkeitsverteilungen mit nur zwei möglichen Ereignissen. Und "zwei" heißt auf lateinisch "bi", weshalb man auch von "Binomialverteilungen" spricht.

Typische Beispiele dafür sind
  • schwarz oder weiß

(wobei "schwarz" das erste und "weiß" das zweite Nomen ist), 

  • wahr oder falsch,
  • bei einer Münze Kopf oder Zahl,
  • ein Schütze trifft ins Schwarze - oder daneben

(es gibt also keine "halbguten" Ergebnisse wie etwa der blaue Ring auf ), 

  • bei Computern Strom oder Nicht-Strom (der sogenannte "binäre Code")

,

  • "du hast die Wahl zwischen Pest und Cholera",
  • : "Sein oder Nichtsein, das ist hier die Frage."

("Halb-[nicht-/tot-]-Sein" wäre etwas Ähnliches wie ).

Da sei doch gleich ergänzt, dass eine solche Aufteilung der Welt in nur zwei Extreme die "Welt" oftmals arg vereinfacht

(vgl. "zweiwertige Logik" und "mehrwertige Logik").

Aus nur zwei Alternativen bestehende Binomialverteilungen kommen oftmals bei Anwendungen vor, haben aber auch, wie wir weiter unten sehen werden, den Vorteil, dass sich viele Rechnungen erheblich vereinfachen.

Am Beispiel des Kartenspiels wird allerdings auch klar, dass wir uns eine kleine Erschwerung eingehandelt haben:

  • es liegt oftmals nicht mehr eine Gleichverteilung vor

( in jedem einzelnen der vier Fälle  , ,und ), 

  • sondern häufig treten zwei unterschiedliche Wahrscheinlichkeiten auf

(z.B. im Fall , aber im Fall "Nicht-"),

wobei sich allerdings die beiden Wahrscheinlichkeiten natürlich immer zu 1 aufaddieren

( + = 1).

Damit aber zurück zu unserer neuen Wahrscheinlichkeitsverteilung: für zweimaliges Ziehen ist das Baumdiagramm erheblich übersichtlicher geworden, da es nur noch jeweils zwei (statt, wie oben noch, vier) neue Abzweigungen gibt:

Nun zwei weitere Festlegung zu unserem Versuch:

  1. Es soll fünf mal (wieder: mit Zurücklegen) gezogen werden, so dass das Baumdiagramm folgendermaßen aussieht:

  1. sei nun gefragt, wie wahrscheinlich es ist, bei fünfmaligem Ziehen drei Mal

(und das bedeutet gleichzeitig zwei Mal ,oder )

zu ziehen.

Nun könnte man all die Wege einzeichnen, die derart zum Ziel führen. Für einen einzigen Fall aus der oberen Hälfte des Baumdiagramms sei das auch mal vorgemacht:

 

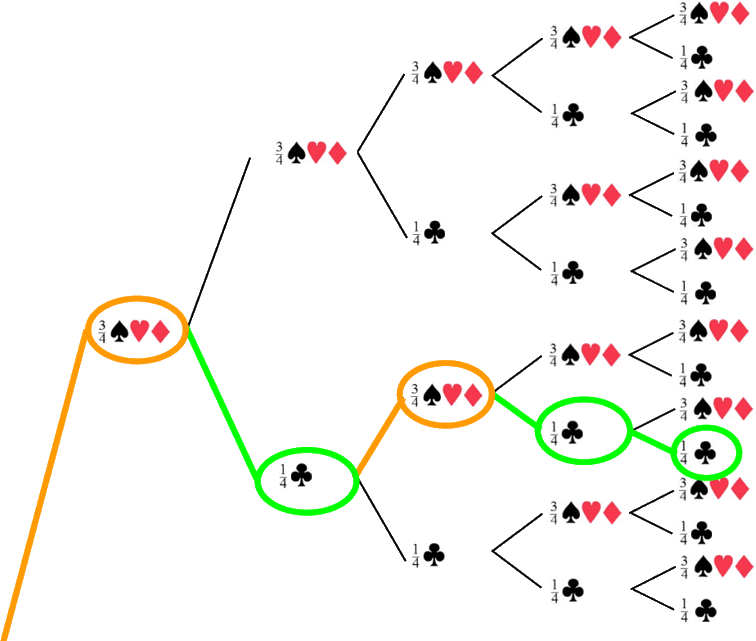
Ich hatte bewusst ein fünfmaliges Ziehen mit fast schon unüberschaubar vielen Möglichkeiten gewählt, denn bei fünfmaligem Ziehen ergeben sich sehr viel mögliche Wege zum Ziel

"drei mal und zwei mal ".

All diese Wege einzuzeichnen, wäre sehr umständlich und wohl auch fehleranfällig

(man übersieht gerne mal etwas).

Schauen wir uns deshalb den einen eingezeichneten Weg genauer an, um daraus zu schließen,

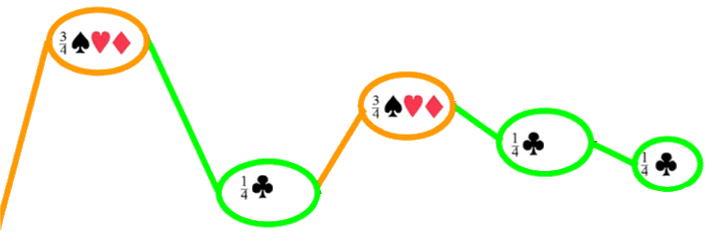
Daraus lassen sich mehrere Schlüsse ziehen:

  1. ist die Wahrscheinlichkeit für diesen Einzelweg

bzw. nach Anwendung des Kommutativgesetzes und von Potenzen

.

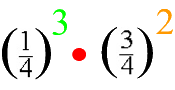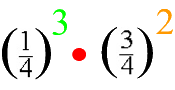  1. ist das Kommutativgesetz ein guter Tipp: es lassen sich ja nicht nur die Zahlen und vertauschen, sondern auch die Ziehungen. So bedeutet eben auch

,

dass also bei den ersten drei Ziehungen (jeweils mit der Wahrscheinlichkeit) und bei den letzten zwei Ziehungen eine der "Farben" (jeweils mit der Wahrscheinlichkeit ) gezogen wurde.

Damit stellt sich die Frage, auf wie viele Arten man die drei grünen Fälle auf die fünf Ziehungen verteilen kann

(und damit automatisch die beiden orangen Fälle auf die restlichen beiden Ziehungen).

Das sind

(weil drei auf fünf Ziehungen zu verteilen sind, aber die Reihenfolge der egal ist)

Fälle, und daraus folgt, dass es insgesamt mögliche Wege gibt. Weil sich aber auf jedem einzelnen dieser Wege (wie gezeigt) die Wahrscheinlichkeit 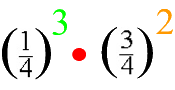ergibt, ist somit die Gesamtwahrscheinlichkeit

.

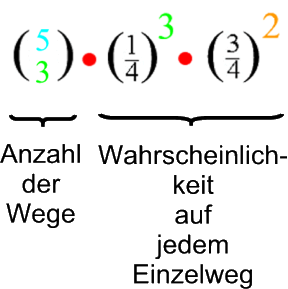  1. Erinnern wir uns nun an zweierlei:

  1. Die 2 in der Formel ist unnötig, da sie sich automatisch als 5 - 3 ergibt. Damit lautet unsere Formel

  1. Die Wahrscheinlichkeit   von und die Wahrscheinlichkeit  von ergänzen sich natürlich zu 1

(eines der beiden Ereignisse oder tritt garantiert ein),

d.h.

+ = 1,

woraus folgt:

= 1 -

(man könnte auch sagen: ist die Restwahrscheinlichkeit, wenn man die Ausgangswahrscheinlichkeit von 1 abzieht).

Mit = 1 - verändert sich unsere Formel nun zu

.

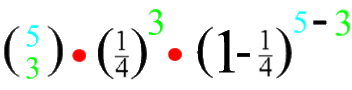Damit  ist nun aber doch auf den ersten Blick alles im Vergleich mit der Ausgangsformel 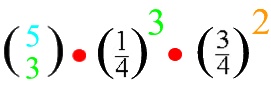nur viel umständlicher geworden.

Immerhin aber hat die Formel

aber den Vorteil, dass in ihr alles ausschließlich von den Ausgangsvoraussetzungen

abhängig ist. Bzw. alles, was mit dem "billige Rest"   zusammenhängt, also

ist rausgeflogen.

Einzig und allein mit der Formel 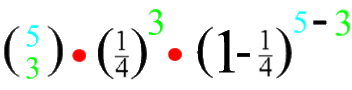sind wir aber in der Lage zu verallgemeinern:

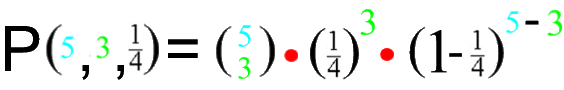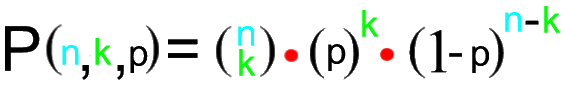
Die allgemeine Formel für Binomialverteilungen lautet also

Es sei noch kurz rekapituliert, wie wir zu dieser Formel gekommen sind:

  1. dadurch, dass wir alles nur in Abhängigkeit von n, k und p ausgedrückt haben,
  2. indem nicht alle Wege abgezählt, sondern anhand eines Weges die Systematik erarbeitet haben,
  3. indem wir "Dinge" (z.B. ()3 ) nie ausgerechnet haben

(vgl. Bild ).

Um nun aber eine anschauliche Vorstellung des Erarbeiteten zu bekommen, kehren wir doch erst mal zum konkreten - Beispiel und zurück.

Wenn wir das nun doch mal ausrechnen, ergibt sich

P(5, 3, ) =  0,087890625

Nun haben wir aber vielleicht vor lauter Rumhantieren oben vergessen, was das eigentlich bedeutet, nämlich

die Wahrscheinlichkeit, mit der ich im obigen Experiment bei fünfmaligem Ziehen drei mal ziehe.

Und genauso können wir das für sämtliche 0 ≤ k ≤ n, also für k = 0, k = 1, k = 2, k = 3, k = 4 und k = 5, tun:

die Wahrscheinlichkeit, mit der ich im obigen Experiment bei fünfmaligem Ziehen 0 mal ziehe:       P(5, 0, ) ≈  0,2372
die Wahrscheinlichkeit, mit der ich im obigen Experiment bei fünfmaligem Ziehen 1 mal ziehe:        P(5, 1, ) ≈  0,3955
die Wahrscheinlichkeit, mit der ich im obigen Experiment bei fünfmaligem Ziehen 2 mal ziehe:       P(5, 2, ) ≈  0,2636
die Wahrscheinlichkeit, mit der ich im obigen Experiment bei fünfmaligem Ziehen 3 mal ziehe:       P(5, 3, ) ≈  0,0878
die Wahrscheinlichkeit, mit der ich im obigen Experiment bei fünfmaligem Ziehen 4 mal ziehe:       P(5, 4, ) ≈  0,0351 
die Wahrscheinlichkeit, mit der ich im obigen Experiment bei fünfmaligem Ziehen 5 mal ziehe:       P(5, 5, ) ≈  0,0009765
Summe:                          1 

Wenn wir uns das nun auf die Schnelle durch ein Computerprogramm darstellen lassen, so ergibt sich

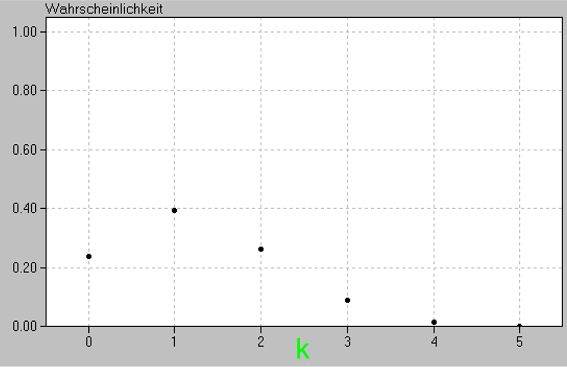
Daran ist nun zweierlei bemerkenswert:

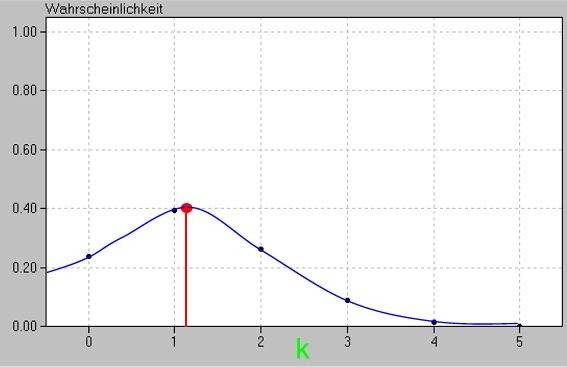
  1. ergibt sich eine (wenn auch bislang nur durch fünf Punkte gestützte) Gaußsche Glockenkurve:

 

Oder allgemein: die grafischen Darstellungen von Binomialverteilungen haben immer die Form einer Gaußschen Glockenkurve.

  1. Die Gaußsche Glockenkurve liegt im vorliegenden Fall aber nicht mittig, sondern nach links verschoben. Und es war ja in der Tat zu erwarten, dass ihr Maximum etwa bei 5 • = 1,25 liegt.

Schauen wir uns nun mit unserem Vorwissen eine besonders einfache Binomialverteilung an, nämlich die Gleichverteilung, d.h. dass jeder der beiden Fälle

(z.B.

mit derselben Wahrscheinlichkeit, also p = (statt bislang p = ), auftritt.

Damit ergeben sich die Wahrscheinlichkeiten

P (5, k, ) = ,

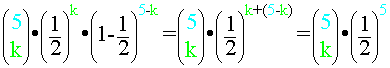was grafisch so aussieht:

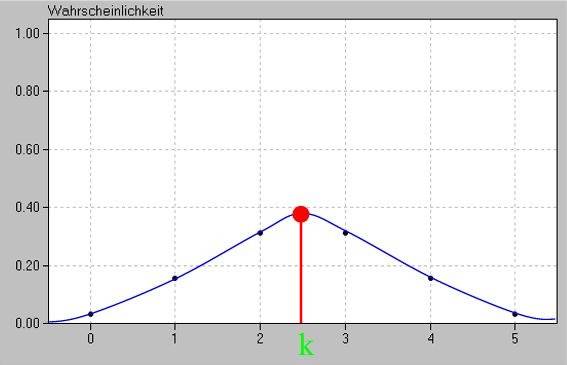
Hier liegt nun die Gaußsche Glockenkurve in der Tat hübsch mittig, und wie zu erwarten liegt ihr Maximum bei 5 • = 2,5.

So mit das berühmteste Beispiel für solch eine Gleichverteilung ist das Galton-Brett, bei dem jede Kugel, wenn sie auf einen Stift fällt, mit derselben Wahrscheinlichkeit nach links oder rechts fällt:

(Nebenbei: die Addition der Wahrscheinlichkeiten funktioniert beim Galton-Brett mit

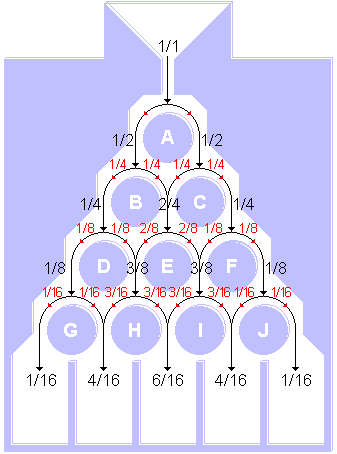
exakt nach derselben Logik wie beim Pascalschen Dreieck

,

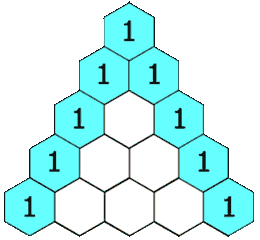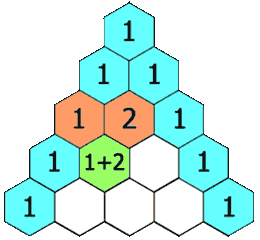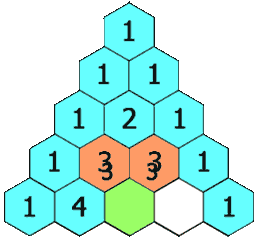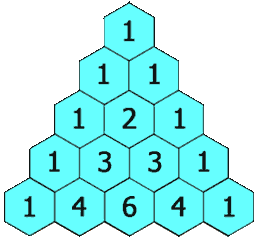in dem ja auch die Binomialkoeffizienten vorkommen:

  . )

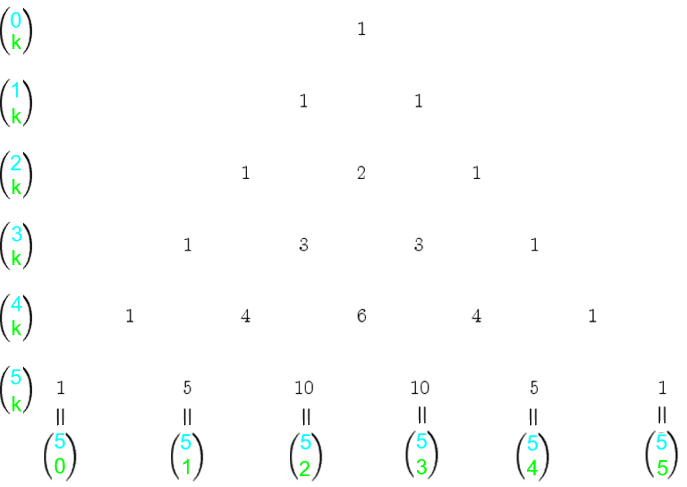Nach all diesen Vorarbeiten rechnen wir nun nicht mehr umständlich, sondern überlassen die Rechnungen und Darstellungen dem sehr empfehlenswerten Computerprogramm "Discrete Distributions", mit dem wir schnell viele Möglichkeiten

(zudem kontinuierlich; vgl. )

durchspielen und vergleichen und somit das grundsätzliche Verhalten von Binomialverteilungen erkunden können.

(Nebenbei: wohl nirgends sonst in der Mathematik sind Computer so sinnvoll wie bei der Wahrscheinlichkeitsrechnung, da dort bei großen Datenmengen doch schnell massenhaft Rechnungen anfallen.)

Vorweg sei noch eine besondere Eigenart des Programms erklärt: es stellt den Bereich 0, 1, 2, 3 ... n auf der x-Achse immer gleich breit dar. Zwei Beispiele:

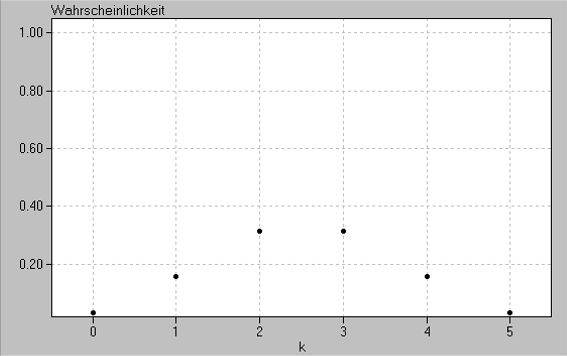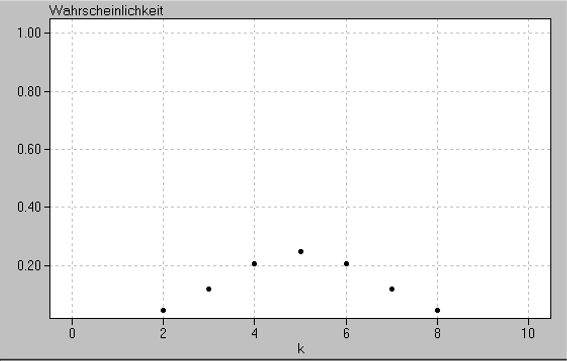obwohl doch eigentlich die Skala auf der x-Achse doppelt so breit wie bei n = 5 sein müsste. 

Grund für diese Normierung ist natürlich, dass auch für große n alle n ins Programmfenster passen sollen

(auf der y-Achse ist das hingegen kein Problem, da die größtmögliche Wahrscheinlichkeit immer 1 ist).

Wichtig bei solch einem Programm ist es, immer nur an einem Parameter zu drehen.

In einem ersten Durchlauf lassen wir also n von 0 bis 20 wachsen, behalten aber p = unverändert bei:

Daraus lässt sich entnehmen: bei festem p (hier ) und größer werdendem n

(einige liegen allerdings so knapp über der x-Achse, dass das Programm sie gar nicht mehr anzeigt), 

(da ja sehr viel mehr Einzelwahrscheinlichkeiten untergebracht werden müssen, die sich zu 1 aufaddieren),

(da der Maßstab für größere n immer kleiner wird)

aber absolut gesehen immer breiter. 

Dass sich bei wachsendem n, aber gleichbleibendem p (fast) nur die Höhe der Gaußschen Glockenkurve ändert, sie aber ansonsten ihre Lage beibehält und nur verfeinert wird, lässt sich mit einer schönen weiteren Einstellungsmöglichkeit des Programms zeigen: man kann dafür sorgen, dass die Höhe immer gleich bleibt, wobei sich natürlich kontinuierlich

(zusätzlich zum Maßstab auf der x-Achse jetzt auch)

der Maßstab auf der y-Achse ändert. Und dann ergibt sich für wachsendes n, aber gleichbleibendes p

In einem zweiten Durchlauf behalten wir nun n unverändert bei (im Folgenden n = 20) und lassen stattdessen p gemächlich von 0 bis 1 laufen:

Daraus lässt sich entnehmen: bei festem n (hier 20 ) und größer werdendem p

(was einen nicht wundern sollte, da ja das Maximum immer bei p • 20 liegt, also für größeres p immer weiter rechts),

Oben war schon angedeutet worden, dass sich mit Binomialverteilungen erheblich einfacher rechnen lässt, was wohl ein Hauptgrund dafür ist, dass sie im Mathematikunterricht so deutlich betont werden.

Insbesondere lassen sich bei Binomialverteilungen

  1. der Erwartungswert μ ,
  2. die Varianz σ2
  3. und die Standardabweichung σ 

sehr einfach berechnen.

(Kleine Zwischennotiz: der Mittel- und der Erwartungswert werden zwar auf dieselbe Weise, nämlich als arithmetisches Mittel berechnet, aber dennoch gibt es einen markanten Unterschied:

Zu a., also dem Erwartungswert μ :

(vgl. )

(ohne dass das hier hergeleitet / begründet wird)

zur simplen Multiplikation

μ = n • p

Zu b., also der Varianz σ2

(vgl. wieder ) 

(wieder ohne dass das hier hergeleitet / begründet wird)

zur simplen Multiplikation

σ2 = n • p •  (1 - p) =

        μ    •  (1 - p)

Zu c., also der Standardabweichung σ :

Wichtiger als die

(hier ja eben gerade nicht vorgeführte)

Herleitung / Begründung ist mir aber die "Interpretation" des Erwartungswertes, der Varianz und der Standardabweichung:

wie oben schon mehrfach vermutet, liegt der Erwartungswert immer beim p-fachen der Gesamtzahl n. Beispielsweise beim obigen Kartenspielbeispiel, also für n = 5 und p = , heißt das, dass μ = 5 • = 1,25:

Nehmen wir wieder das Kartenspielbeispiel mit n = 5, p = sowie, wir wir inzwischen ja wissen,  μ = 1,25.

Damit ergibt sich für die Varianz σ2 = 1,25 • (1 - ) = 1,25 • = 0,9375 und somit für die Standardabweichung σ ≈ 0,9682:

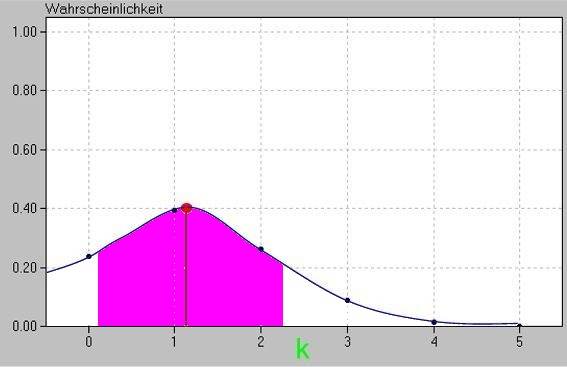
Wenn wir nun p in vergrößern, ergibt sich

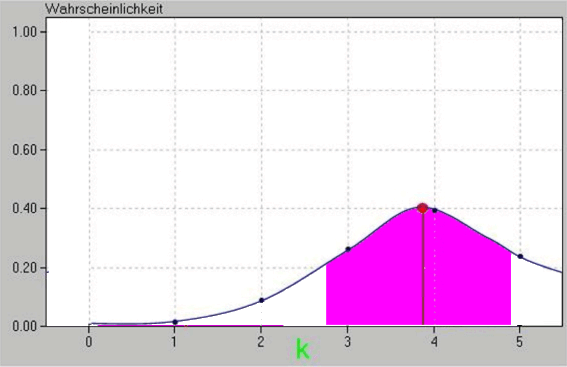
Indem also bei der Varianz σ der Erwartungswert μ mit (1 - p) multipliziert wird,

(auch das ist ein Zeichen dafür, dass der Graph zwar wandert, aber [weitgehend] seine Form beibehält).

Wenn man allerdings ganz genau ist, muss man formulieren:

Denn beispielsweise für n = 5 und p = 0,3 ergeben sich μ = 5 • 0,3 = 1,5 und dann σ2 = 1,5 • 0,7 = 1,05 und somit eine leicht unterschiedliche Varianz und eine andere Standardabweichung.

Auf jeden Fall ist (1 - p) aber die "ausgleichende Gerechtigkeit" :