 hebt sich jedes Jahr um 4 cm
hebt sich jedes Jahr um 4 cm
oder

| |
Obwohl der Name in der Mathematik schon anderweitig für erheblich Anspruchsvolleres vergeben ist
(vgl.


 ), ),
nennen einige Leute das, was wir im Folgenden treiben, auch großspurig "Transformation von Funktionen".
Man kann das tun, aber natürlich auch
(zumindest im Unterricht)
sein lassen. |
Zwecks Anschaulichkeit ist mir manchmal danach, grob unmathematisch zu argumentieren, also z.B. beim "Binomi"
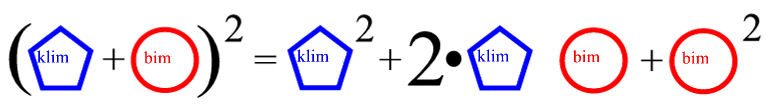
(vgl. 

 ).
).
Worum es geht, sind einige absolut zentrale und doch offensichtlich für viele SchülerInnen enorm schwierige mathematische Grundlagen:
- die Funktionsweise des Koordinatensystems
(vgl.  ),
),
- wie Funktionsgraphen im Koordinatensystem
entstehen,
- was Parameteränderungen am Funktionsgraphen verändern.
Jüngst (1/2010) habe ich im Radio gehört,

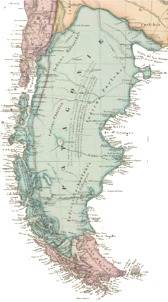
Patagonien
hebe sich mit dem für geologische Zeiträume ungeheuren Tempo von 4 cm pro Jahr. Grund dafür sei, dass wegen der abnehmenden Gletscher weniger Gewicht auf den Landmassen liege.
Da frage ich mich natürlich gleich
"Ganz Gallien ist von den Römern besetzt... Ganz Gallien? Nein! Ein von unbeugsamen Galliern bevölkertes Dorf hört nicht auf, dem Eindringling Widerstand zu leisten."
bzw. analog "ganz Patagonien?" Patagonien ist riesig und, wenn ich's richtig verstanden habe, nur ganz im Süden (ehemals) eisbedeckt. Kommt hinzu, dass sich wohl kaum ganz Patagonien gleichmäßig hebt. d.h. überall um exakt 4 cm.
Und dennoch sei im Folgenden der Einfachheit mal davon ausgegangen, dass sich ganz Patagonien pro Jahr gleichmäßig um 4 cm hebt, d.h. egal, ob es


aussieht.
Gleichmäßige Hebung um 4 cm bedeutet nun aber, dass jeder Punkt
(egal, wie hoch er bislang lag)
um 4 cm nach oben wandert
(im Folgenden nicht maßstabgerecht):
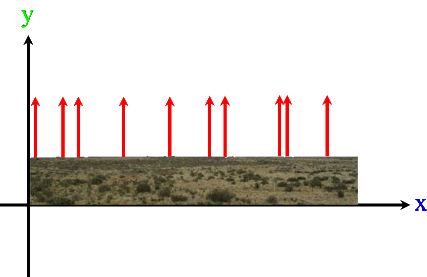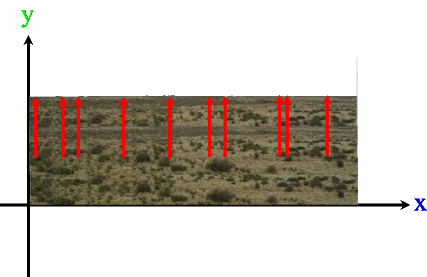
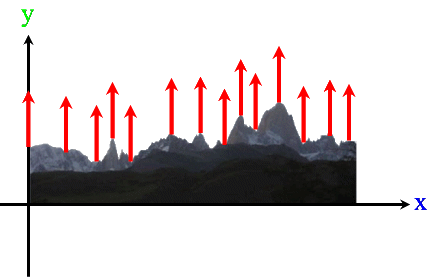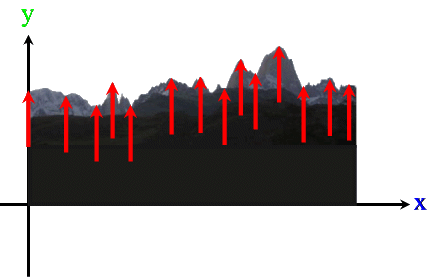
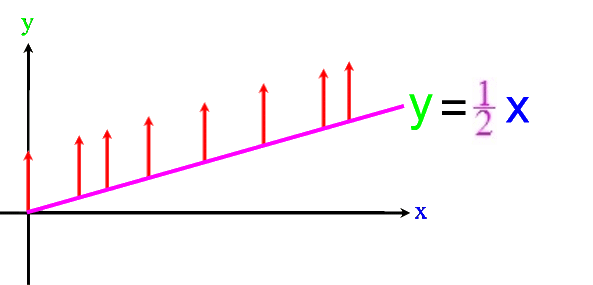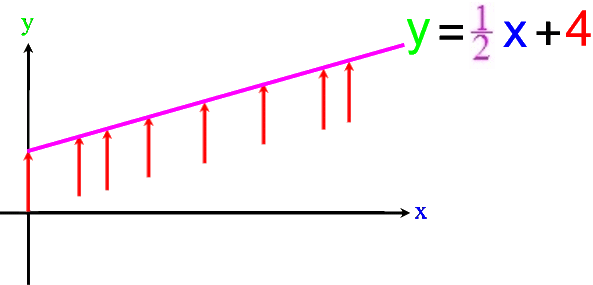
Nun kann man natürlich nicht nur Patagonien anheben, sondern es ist herzhaft egal, was da um 4 (cm) angehoben wird, also z.B.
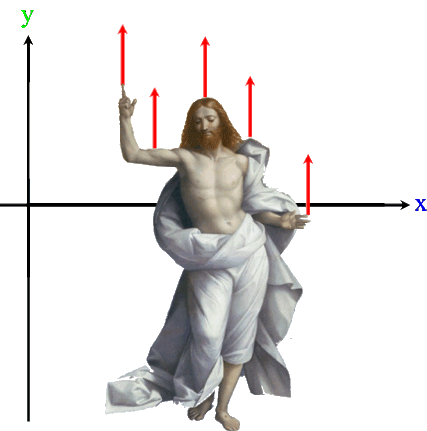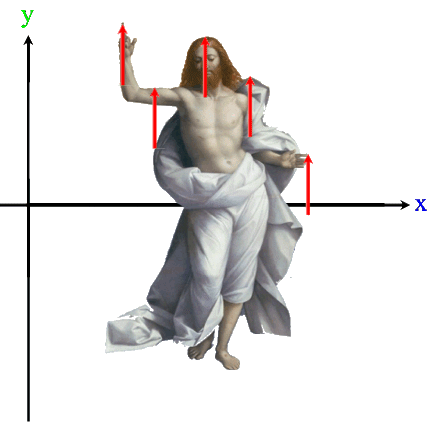
Oder wir nennen das, was da angehoben wird, möglichst allgemein
(und nichtssagend)
"Dingsbums". Und da uns im Folgenden insbesondere Funktionen interessieren, diese aber immer von der unabhängigen Variablen x abhängig sind, ergänzen wir zu "Dingsbums (x)":

Wenn wir das nun exemplarisch auf zwei einfache mathematische Funktionen anwenden, so ergibt sich
- für die Ausgangsfunktion f:
y =
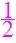 x :
x :
- für die Ausgangsfunktion f:
y = x
2 :
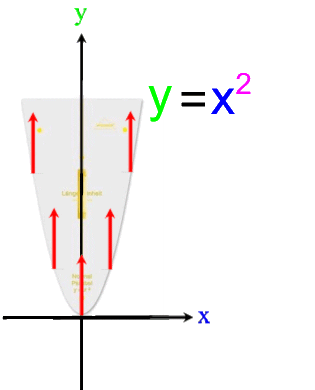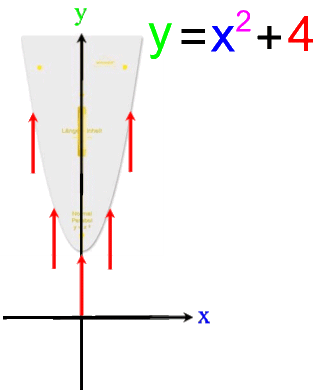
Die Anhebung Patagoniens erinnert an die
"Hebung riesiger Faltengebirge durch Kollision zweier Kontinentalplatten (zum Beispiel Himalaya, Alpen)."
(Quelle:  )
)
"Kollision" deutet schon an, dass ganze Kontinentalplatten sich seitlich aufeinander zu bewegen:

Eines der eindrücklichsten Beispiel für solch eine seitliche Bewegung von Platten ist die Inselkette von  Hawaii:
Hawaii:

Da bewegt sich eine unterseeische Platte nordwestlich
(auf dem Bild nach links oben)
über einen feststehenden sogenannten  "Hotspot" hinweg, aus dem Lava hervorquillt, über dem also Vulkane entstehen. Und so sind nacheinander die Inseln von links oben nach rechts unten
"Hotspot" hinweg, aus dem Lava hervorquillt, über dem also Vulkane entstehen. Und so sind nacheinander die Inseln von links oben nach rechts unten
(heutiges "Hawaii", auch "Big Island" genannt)
entstanden. Der heutzutage höchste Vulkan Hawaiis
(und nebenbei, vom unterseeischen Boden aus gemessen, der höchste Berg der Welt!)
ist der wegen seiner Flachheit allerdings wenig spektakuläre

 Mauna Loa auf "Big Island".
Mauna Loa auf "Big Island".
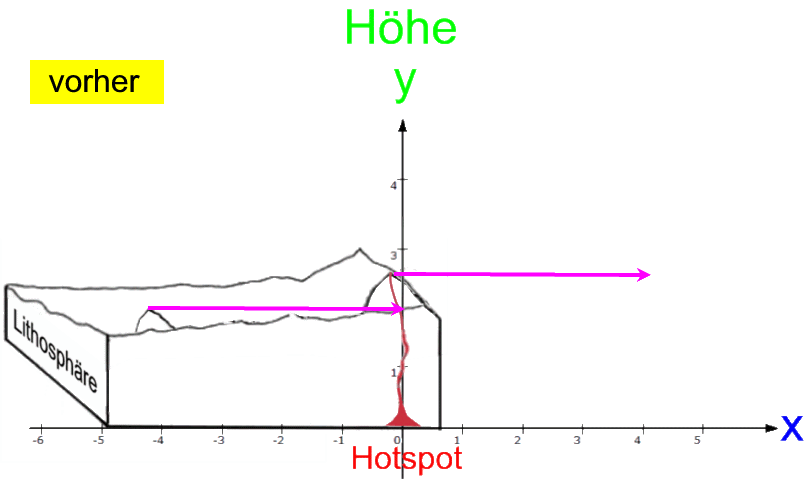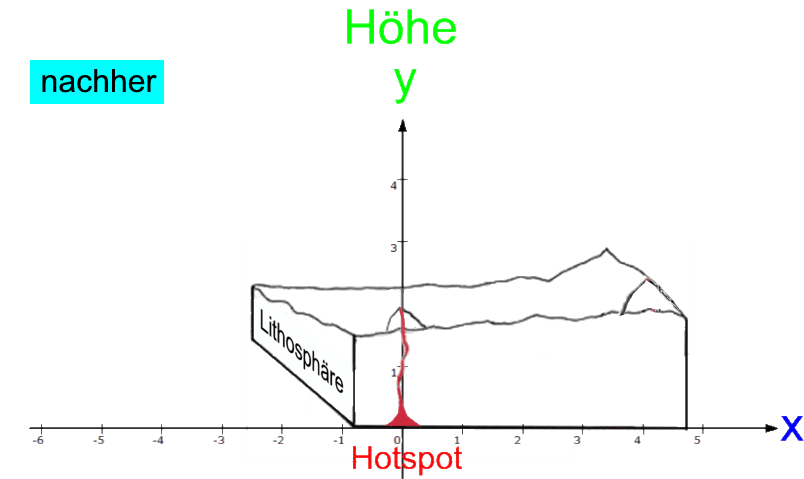
Nun werden zwar die nacheinander entstehenden Vulkane zum jeweiligen Zeitpunkt ihrer Entstehung nicht alle exakt gleich hoch gewesen sein. Vor allem aber: die früher entstandenen sind natürlich inzwischen durch die Erosion kleiner geworden. Dieser Erosionseffekt sei aber im Folgenden nicht berücksichtigt, d.h. wir gehen der Einfachheit halber davon aus, dass alle Vulkane von Anfang an ihre heutige Höhe hatten.
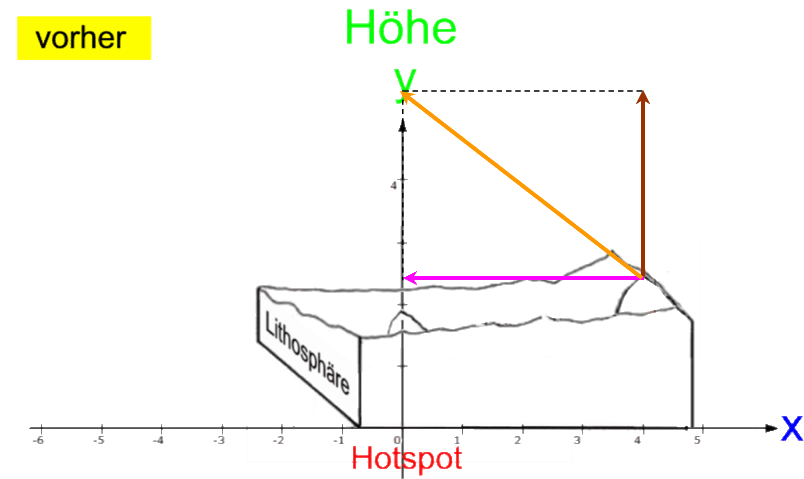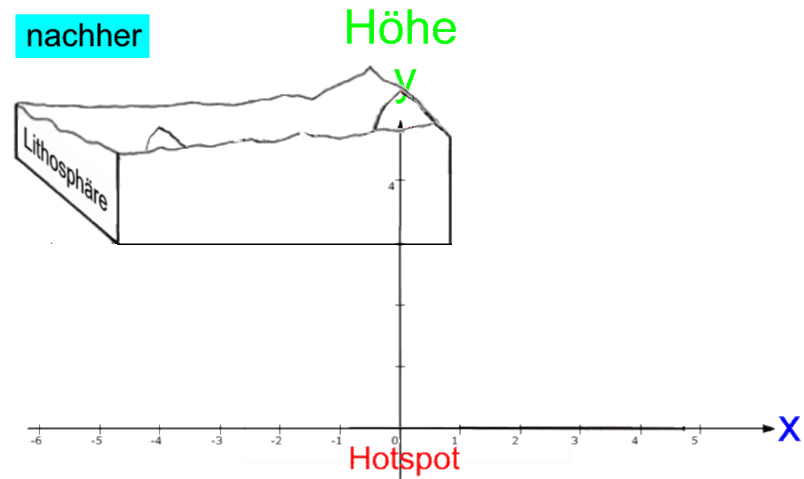
Da der Hotspot
(im Gegensatz zur "Platte" [der sogenannten "Litosphäre"] samt den Vulkanen)
fest steht, legen wir ihn in den Ursprung eines Koordinatensystems, und dann ergibt sich diese Abfolge:
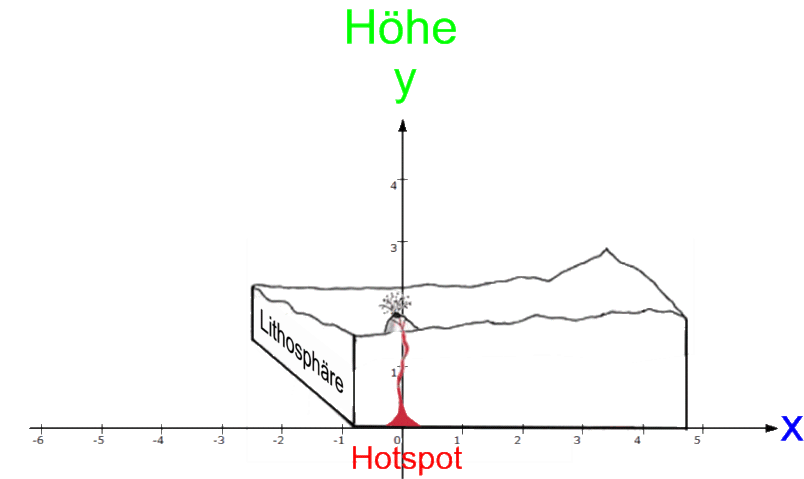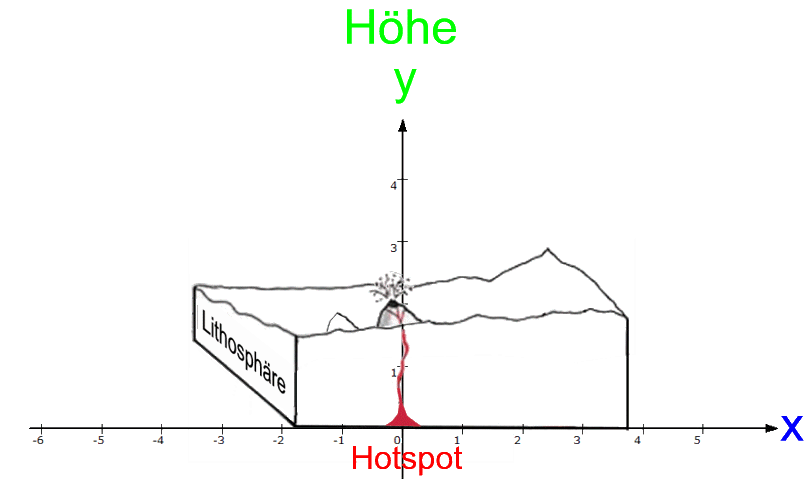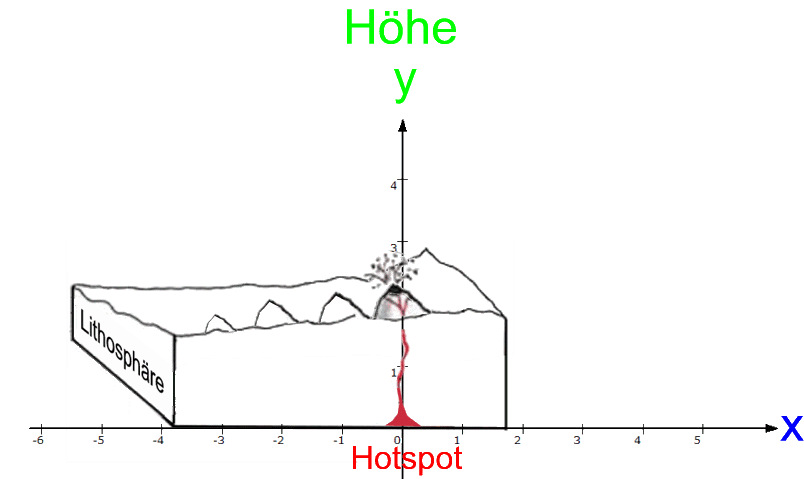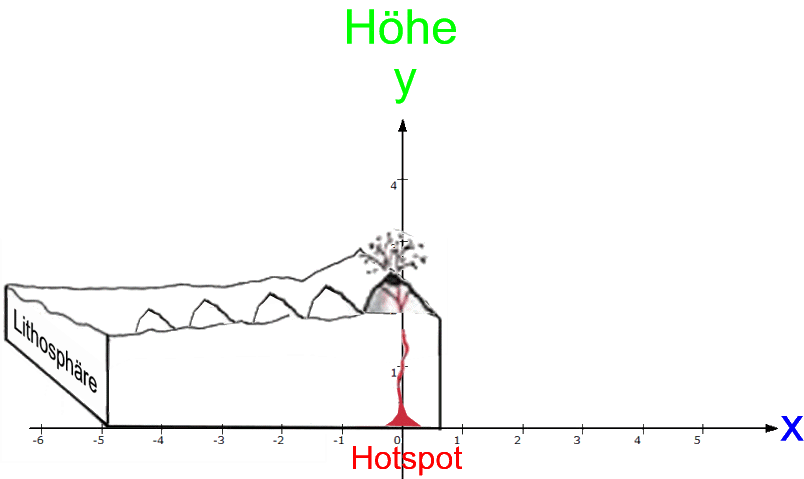
Das sei nun in zweierlei Beziehungen noch weiter vereinfacht:
- schauen wir uns nur den zuerst und den
zuletzt entstandenen Vulkan an,
- tun wir so, als seien beide schon immer
vorhanden gewesen.
Damit ergibt sich dann:
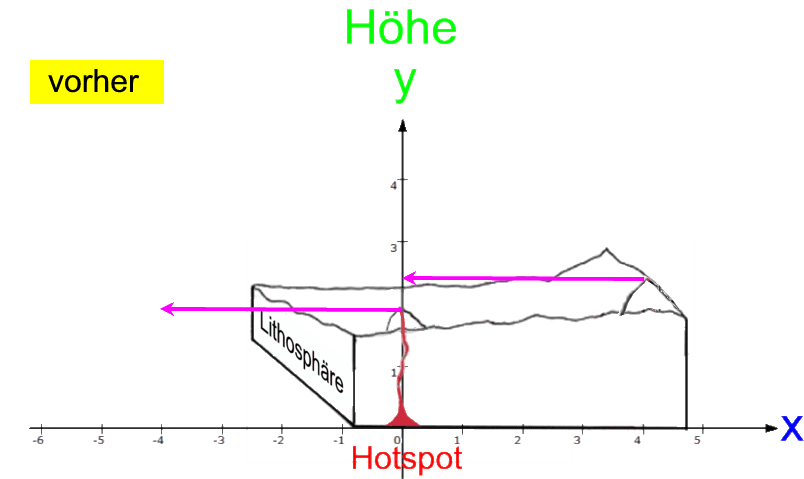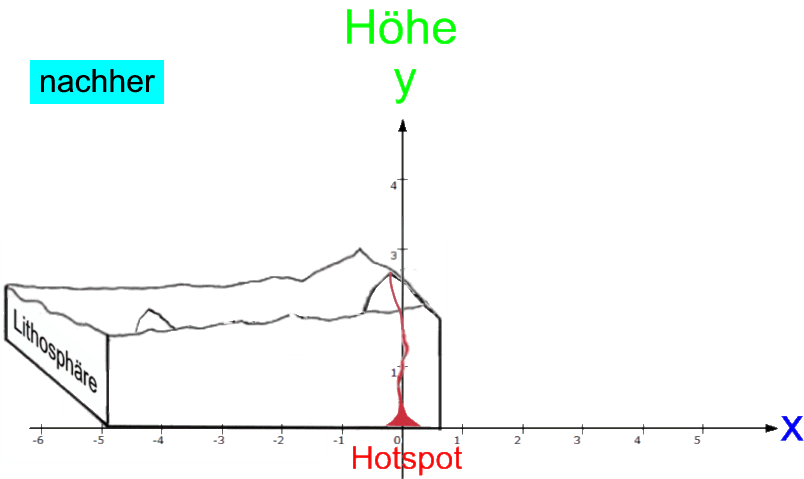
Also befindet sich,
- der Berg, der bisher bei
x = 4 lag, nun bei
x = 0,
- der Berg, der bisher bei
x = 0 lag, nun bei
x = -4.
Wenn also
- f die Funktion
vor der Verschiebung und
- g die Funktion
nach der Verschiebung ist,
so gilt
= f( 0+4) ,
= f(-4+4).
Oder allgemein wird die Lage jedes Punkts nach der Verschiebung dargestellt durch
f ( x + 4 ) .
Hier liegt nebenbei eine hübsche Fehlerquelle vor: obwohl die Inseln ins Negative (nach links) verschoben werden, muss es dennoch (oder gerade deswegen) "plus" heißen.
Den Grund für dieses "plus"
(und für "gerade deswegen")
kann man besser erkennen, wenn man mal probeweise die umgekehrte Bewegungsrichtung annimmt:
(... also die in der Mathematik normale Bewegungsrichtung, nämlich immer vom Negativen [links] ins Positive [rechts]).
Jetzt haben die Berge
- schon
vorher die Höhe,
- die sie erst
nachher, d.h. um
4 weiter rechts, haben werden,
- d.h. sie sind sozusagen ihrer Zeit um +4 voraus.
Nun finden die horizontale und die vertikale Plattenbewegung aber nicht immer streng getrennt
(also unabhängig voneinander oder nacheinander)
statt, sondern oftmals gleichzeitig statt. Z.B.:
- weil Afrika horizontal in Europa reinknallt, falten sich gleichzeitig
die Alpen vertikal auf,
- weil der indische Subkontinent horizontal in Asien reinknallt, faltet sich
gleichzeitig der Himalaya vertikal auf.
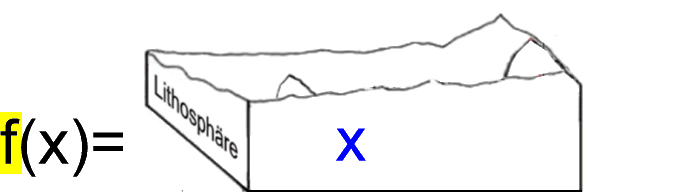
Es ist also auch eine gleichzeitige Bewegung nach links und nach oben statt, also z.B. um 4 nach links und um 3 nach oben:
Wenn nun
bzw.
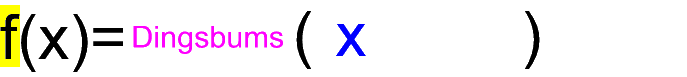
die Funktionsgleichung für die Landschaft vorher ist, so ist

bzw.
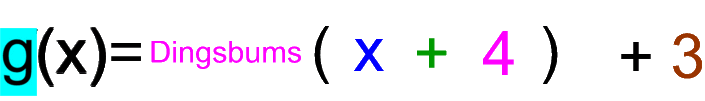
die Funktionsgleichung für die gleichzeitig horizontal und vertikal verschobene Landschaft nachher.
Wichtig dabei ist vor allem, dass die Landschaft/Funktion nachher dieselbe Form hat wie die vorher, nur dass sie woanders liegt.











Kommen wir nun aber zu Veränderungen der Form.
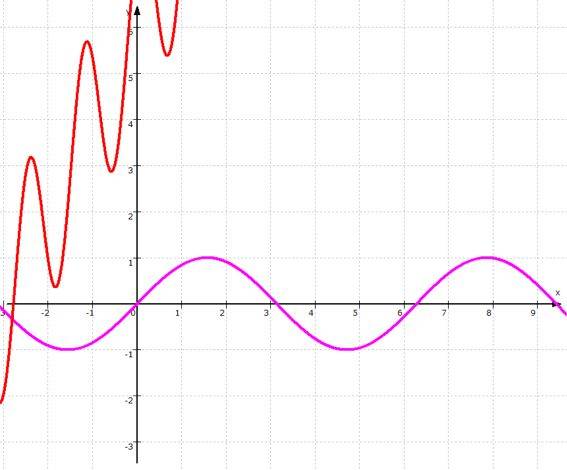
Der Einfachheit halber nehmen wir nun nicht mehr die Hawaii-Landschaft, sondern die Sinus-Funktion. Dabei ist es vielleicht sogar gut, wenn man nicht(mehr) weiß, wie sie zustande kommt, sondern nur ihr Aussehen kennt. Denn dann wirkt die Sinus-Funktion nur um so mehr wie ein festes "Dingsbums".
Hier also der Graph der Sinusfunktion f: y = sin (x):
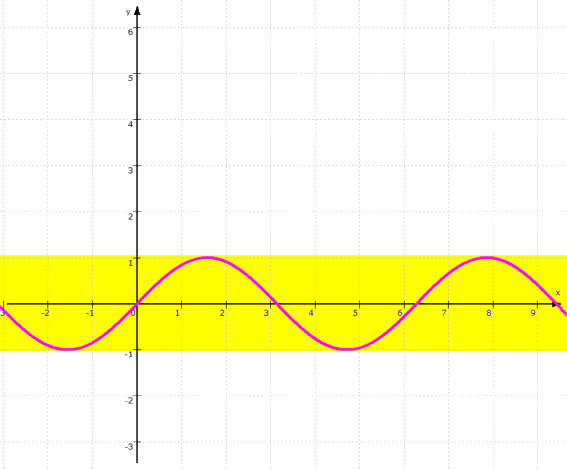
Der Graph der Sinus-Funktion erinnert an sanfte Wellen und ist somit wohl eine besonders schöner Graph, der alle Kriterien für Schönheit erfüllt:
- ist er nach oben und unten
beschränkt, d.h. er wird nie größer als +1 und kleiner als -1,
- ist er beruhigend periodisch,
- ist die Funktion "stetig", d.h. mit einem einzigen "harmonischen" Strich zeichenbar,
- ist die Funktion überall "differenzierbar", d.h. sie hat - vereinfacht gesagt - keine störenden Knicke oder Sprünge
(der Graph ist keine "brechende" Welle  , was nebenbei
, was nebenbei
[da mehrere Punkte übereinander liegen bzw. die Welle rückwärts
(erst nach rechts und dann doch wieder nach links)
läuft]
nicht mal der Graph einer Funktion wäre).
Bevor wir nun aber zur Änderung der Form kommen, wiederholen wir kurz anhand der Sinus-Funktion, was wir oben
(nocht nicht zur Form-, sondern bislang nur zur Lageänderung)
hergeleitet haben:
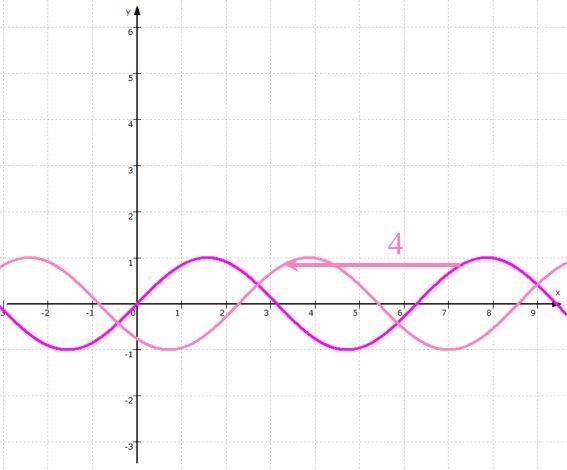
- die horizontale Verschiebung um
4 nach links:
- Ausgangsfunktion
f: y = sin (x
) ,
- verschobene
Funktion g: y =
sin (x
+
4) :
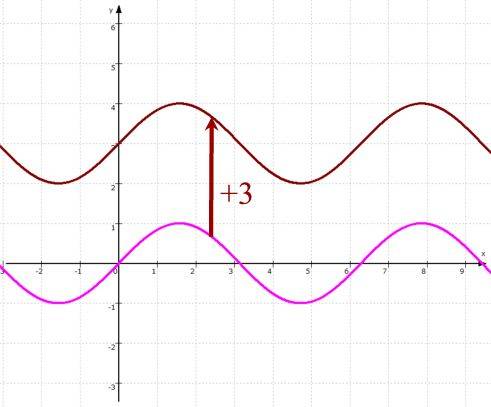
- die vertikale Verschiebung um 3 nach oben:
- Ausgangsfunktion f: y =
sin (x) ,
- verschobene Funktion g: y = sin (x) +
3 :
Im nächsten Schritt soll nun die Sinus-Funktion
- nicht "um" 3 nach oben verschoben werden,
- sondern 2 "mal" so hoch werden, was bedeutet:
(wandert nicht "um" 2 nach oben),
-
insbesondere heißt das: Nullstellen
0 (Schnittpunkte mit der x-Achse), bei denen der y-Wert Null ist, wandern überhaupt nicht, sondern bleiben unverändert.
Daraus folgt
- Vervielfachung mit 2:
- Ausgangsfunktion
f: y =
sin (x) ,
- vervielfachte Funktion g: y = 2
• sin (x) :
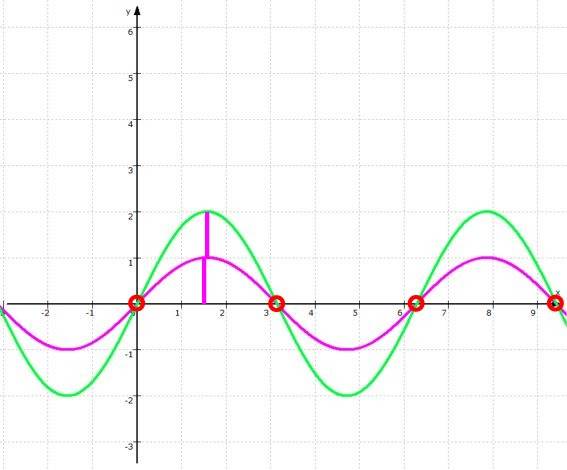
... womit wir erstmals eine Formveränderung haben.
- höhere Frequenz (alle y-Werte werden
schneller nacheinander angenommen):
- Ausgangsfunktion
f: y = sin ( x) ,
- "schnellere" Funktion g: y = sin (5 • x) :
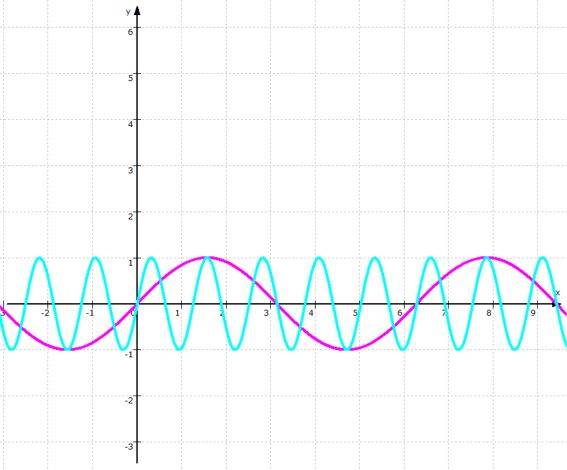
... was wieder eine Formveränderung ist.
- Angenommen des weiteren, die
Sinus-Kurve soll
(ganz widernatürlich)
von links nach rechts den Berg hinauf fließen. Wir erreichen das, indem wir zu ihr eine simple linear steigende Funktion, nämlich h: y = x, addieren
. Die zusamengesetzte Funktion g ergibt sich dann dadurch, dass für alle x-Werte
- die zugehörigen y-Werte der
Sinus-Funktion f und
- die zugehörigen y-Werte der
linearen Funktion h
addiert werden:
- Ausgangsfunktion f: y =
sin (x) ,
- lineare Funktion h: y =
x ,
- zusammengesetzte Funktion g: y = sin (x) +
x
:
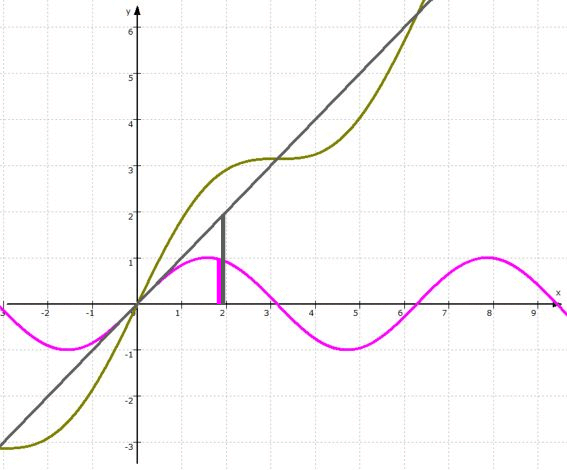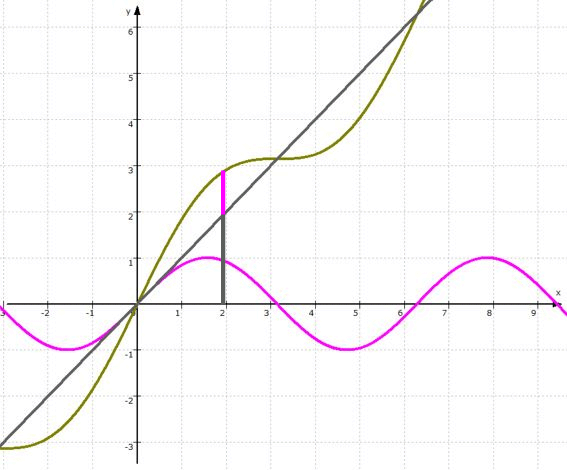
... womit auch wieder eine Formveränderung erfolgt ist.
Nun seien all die Veränderungen 1.-5. gleichzeitig durchgeführt:
- • Ausgangsfunktion f: y =
sin ( x ) ,
• zusammengesetzte Funktion g: y = 2 • [sin (5• x+4
x+4 +3] + x :
+3] + x :
Oder allgemein für "Dingsbums":
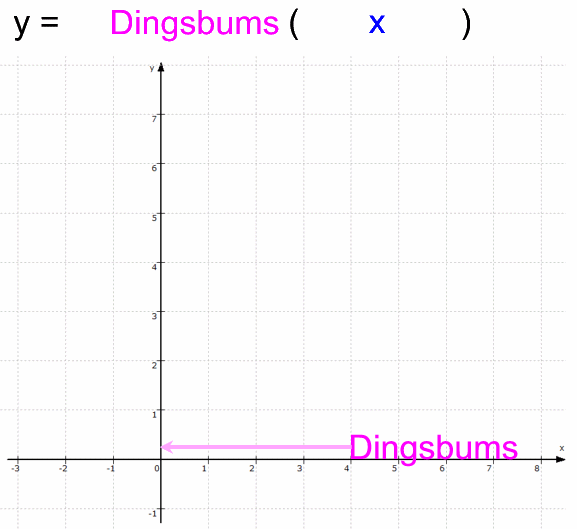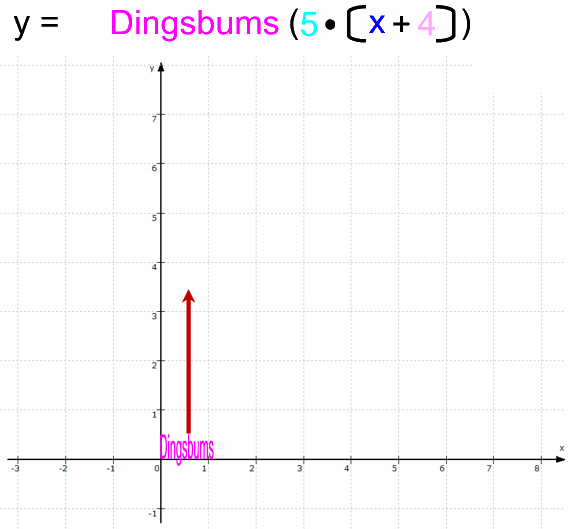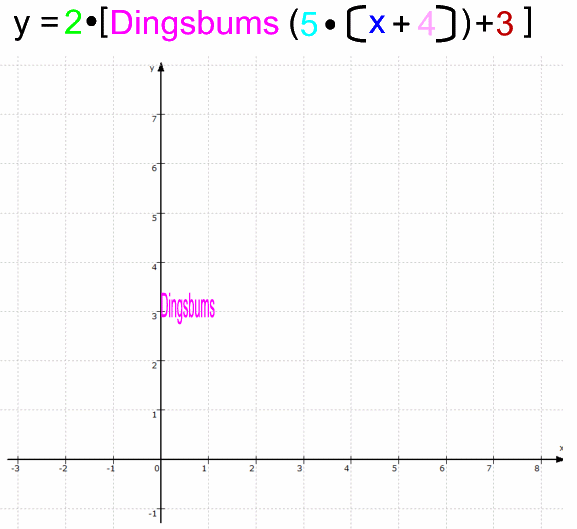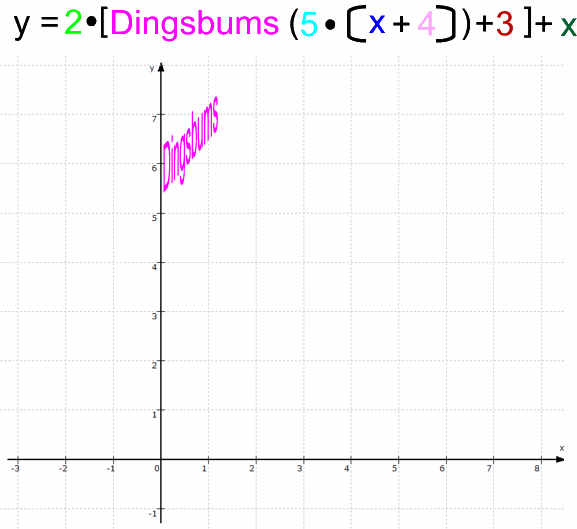
Dabei ist unbedingt die Reihenfolge wichtig, also z.B.
g: y = 2 • [Dingsbums (5 •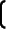 x+4
x+4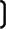 ) +3] + x
) +3] + x
etwas ganz Anderes als
h: y = 2 • [Dingsbums (5• x+4 ) +3 + x ]:
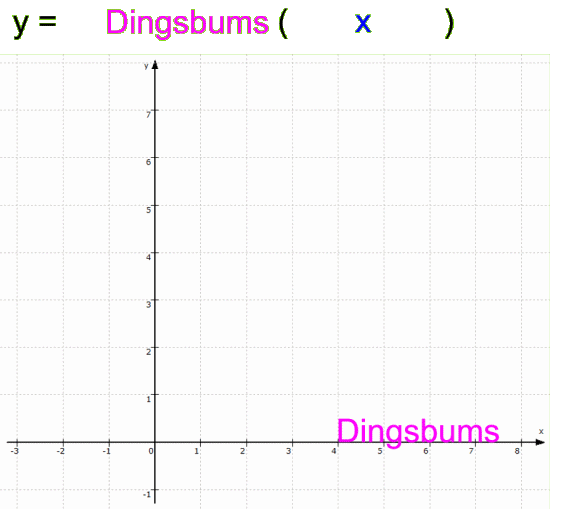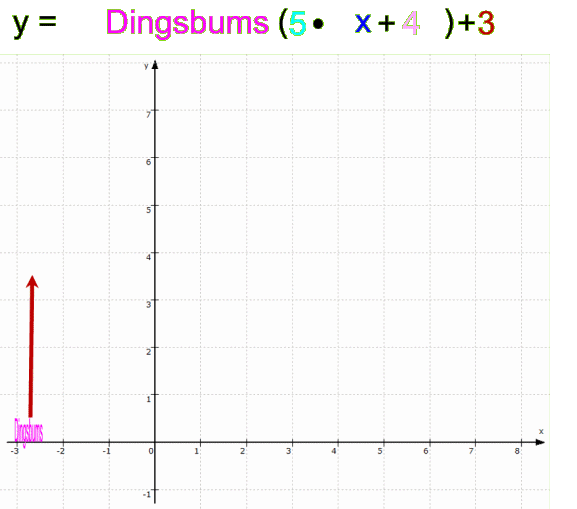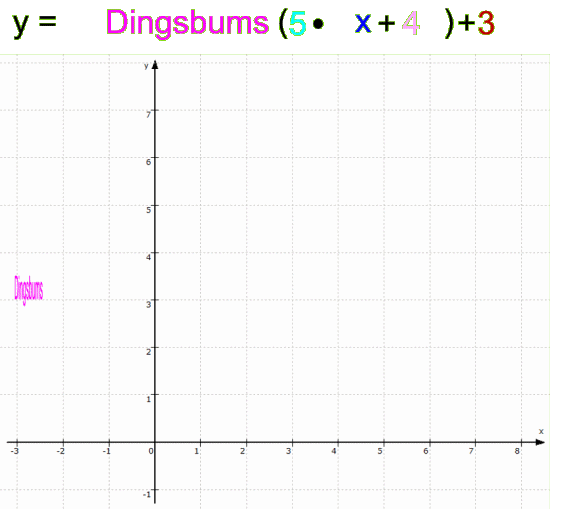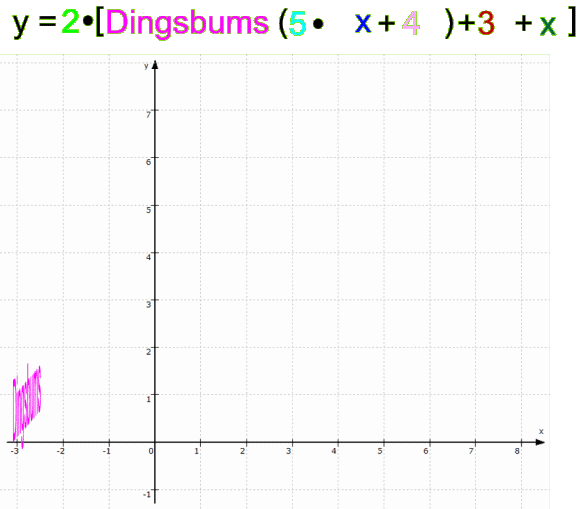
(All das funktioniert allerdings eigentlich nur, wenn "Dingsbums" ein Ausschnitt aus "...DingsbumsDingsbumsDingsbums..." ist.)
Zuguterletzt die rabiate mathematische Abmagerungskur:

| PS: |
Mit Mathematik ist alles so einfach:
Wie fängt man einen Löwen in der Wüste?
[...] Mathematische Methoden
Die triviale Methode:
Man geht in die Wüste, baut einen Käfig, setzt sich rein und definiert: Ich bin außen! Die Hilbertsche oder axiomatische Methode:
Man stellt einen Käfig in die Wüste und führt folgendes Axiomsystem ein:
Axiom 1: Die Menge der Löwen in der Wüste ist nicht leer.
Axiom 2: Sind Löwen in der Wüste, so ist auch ein Löwe im Käfig.
Schlussregel: Ist p ein richtiger Satz, und gilt "wenn p, so q", so ist auch q ein richtiger Satz.
Satz: Es ist ein Löwe im Käfig. Die geometrische Methode:
Man stelle einen zylindrischen Käfig in die Wüste.
1 Fall: Der Löwe ist im Käfig. Dieser Fall ist trivial.
2 Fall: Der Löwe ist außerhalb des Käfigs. Dann stelle man sich in den Käfig und mache eine Inversion an den Käfigwänden. Auf diese Weise gelangt der Löwe in den Käfig und man selbst nach draußen.
Achtung: Bei Anwendung dieser Methode ist dringend darauf zu achten, dass man sich nicht auf den Mittelpunkt des Käfigbodens stellt, da man sonst im Unendlichen verschwindet. Die Projektionsmethode:
Ohne Beschränkung der Allgemeinheit nehmen wir an, dass die Wüste eine Ebene ist. Wie projizieren diese auf eine Gerade durch den Käfig, und die Gerade auf einen Punkt im Käfig. Damit gelangt der Löwe in den Käfig. Die mengentheoretische Methode:
Die Punkte in der Wüste lassen sich wohlordnen. Ausgehend vom kleinsten Element erwischt man den Löwen durch transfinite Induktion.
Bemerkung: Diese Methode ist in Fachkreisen umstritten, wegen der Verwendung des Wohlordnungssatzes bzw. des Auswahlaxioms. Wie so oft, hat auch die vorliegende Fragestellung zu einer fruchtbaren Entwicklung geführt. Dabei wurde schließlich eine sehr viel einfachere Methode entdeckt, die den genannten Mangel nicht aufweist: Man betrachte alle Teilmengen der Wüste, die den Löwen enthalten und bilde den Durchschnitt. Er enthält als einziges Element den Löwen. (Bei dieser Durchschneiderei ist lediglich darauf zu achten, dass das schöne Fell des Löwen nicht zerschnitten wird!) Die Peano - Methode:
Man konstruiert eine Peano - Kurve, die durch jeden Punkt der Wüste geht. Es ist gezeigt worden, dass man eine solche Kurve in beliebig kurzer Zeit durchlaufen kann. Mit dem Käfig unterm Arm durchlaufe man die Kurve in kürzerer Zeit, als der Löwe benötigt, um sich um seine eigene Länge fortzubewegen. Die Bolzano - Weierstraß - Methode
Wir halbieren die Wüste in Nord- Süd Richtung durch einen Zaun. Dann ist der Löwe entweder in der westlichen oder östlichen Hälfte der Wüste. Wir wollen annehmen, dass er in der westlichen Hälfte ist. Daraufhin halbieren wir diesen westlichen Teil durch einen Zaun in Ost-West Richtung. Der Löwe ist entweder im nördlichen oder im südlichen Teil. Wir nehmen an, er ist im nördlichen. Auf diese Weise fahren wir fort. Der Durchmesser der Teile, die bei dieser Halbiererei entstehen, strebt gegen Null. Auf diese Weise wird der Löwe schließlich von einem Zaun beliebig kleiner Länge eingegrenzt.
Achtung: Bei dieser Methode achte man darauf, dass das schöne Fell des Löwen nicht beschädigt wird. Die funktionalanalytische Methode
Die Wüste ist ein separabler Raum. Er enthält daher eine abzählbar dichte Menge, aus der eine Folge ausgewählt werden kann, die gegen den Löwen konvergiert. Mit einem Käfig auf dem Rücken, springen wir von Punkt zu Punkt dieser Folge und nähern uns so dem Löwen beliebig genau. Die topologische Methode
Der Löwe kann topologisch als Torus aufgefasst werden. Man transportiere die Wüste in den vierdimensionalen Raum. Es ist nun möglich die Wüste so zu deformieren, dass beim Rücktransport in den dreidimensionalen Raum der Löwe verknotet ist. Dann ist er hilflos.
Die Banachsche oder iterative Methode
Es sei f eine Kontraktion der Wüste in sich mit Fixpunkt x0. Auf diesen Fixpunkt stellen wir den Käfig. Durch sukzessive Iteration W(n+1) = f (W(n)), n=0,1,2,... ( W(0)=Wüste ) wird die Wüste auf den Fixpunkt zusammengezogen. So gelangt der Löwe in den Käfig. Die Kompaktheitsmethode:
Die Wüste wird ohne Beschränkung der Allgemeinheit als kompakt vorausgesetzt. Man überdecke sie mit einer Familie von Käfigen K(i). Dann gibt es unter ihnen endlich viele Käfige K(j), die bereits die ganze Wüste überdecken. Die Durchmusterung dieser Käfige auf darin befindliche Löwen wird als Diplomarbeit vergeben. Die stochastische Methode:
Man benötigt dazu ein Laplace - Rad, einige Würfel und eine Gaußsche Glocke. Mit dem Laplace - Rad fährt man in die Wüste und wirft mit den Würfeln nach dem Löwen. Kommt er dann wutschnaubend angerannt, so stülpt man die Gaußsche Glocke über ihn. Unter ihr ist er mit der Wahrscheinlichkeit eins gefangen. Die metrische Methode
Wir stellen einen Käfig in die Wüste, verlassen diese unauffällig und definieren in ihr die indiskrete Metrik, d.h. der Abstand zwischen allen Punkten ist 0. Insbesondere ist also der Abstand zwischen Löwe und Käfig gleich 0, d.h. der Löwe ist im Käfig. Die induktive Methode
Ein Löwe sei in der Wüste. Mit vollständiger Induktion zeigt man leicht, dass für beliebige n Element N gilt: n Löwen sind in der Wüste. Weil die Wüste endlichdimensional ist, liegen die Löwen für hinreichend große n überall dermaßen dicht, dass zwangsläufig einer in den Käfig gedrängt wird. (Quelle:
 ) ) |
 hebt sich jedes Jahr um 4 cm
hebt sich jedes Jahr um 4 cm
 hebt sich jedes Jahr um 4 cm
hebt sich jedes Jahr um 4 cm









![]() )
)
![]() Hawaii:
Hawaii:
![]() "Hotspot" hinweg, aus dem Lava hervorquillt, über dem also Vulkane entstehen. Und so sind nacheinander die Inseln von links oben nach rechts unten
"Hotspot" hinweg, aus dem Lava hervorquillt, über dem also Vulkane entstehen. Und so sind nacheinander die Inseln von links oben nach rechts unten




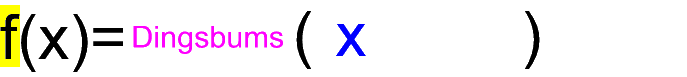

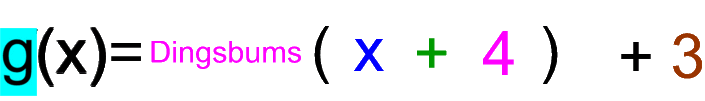












 , was nebenbei
, was nebenbei




![]() x+4
x+4![]() +3] + x :
+3] + x :
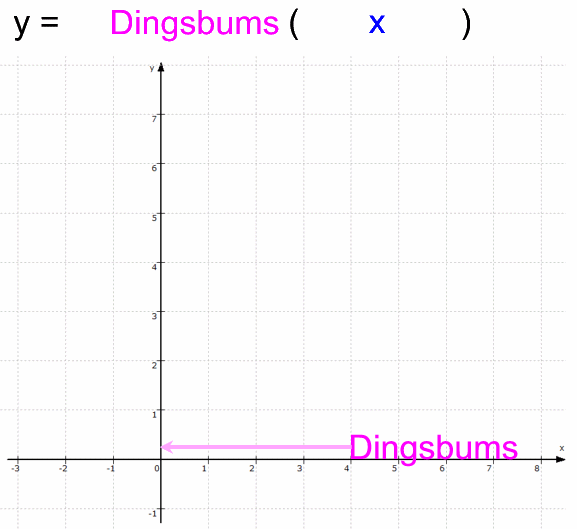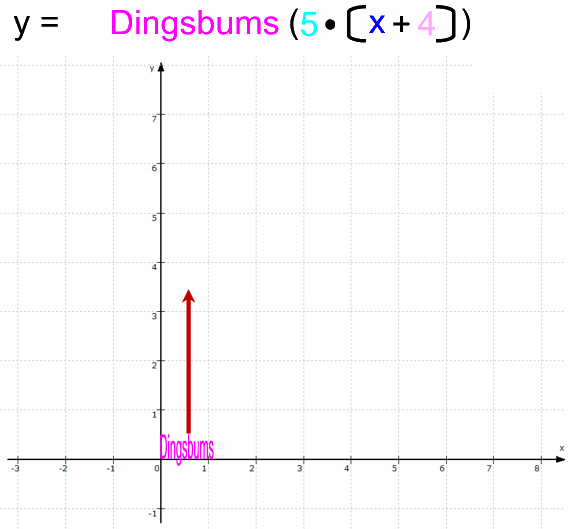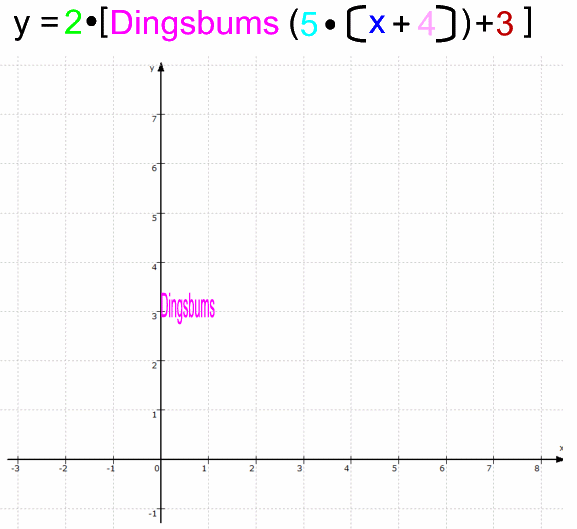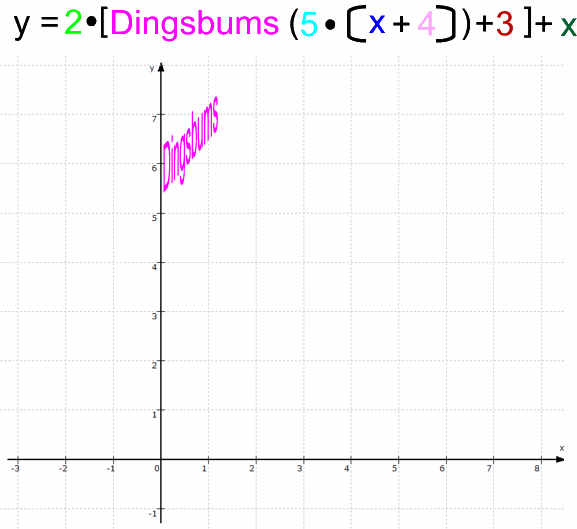
![]() x+4
x+4![]() ) +3] + x
) +3] + x
