aus dem Film

Vorbemerkungen
Hauptteil

Vorbemerkungen 

Zwischen 1948 und 1963 hat Giovanni Guareschi für ein Satiremagazin viele Don-Camillo-und-Peppone-Erzählungen geschrieben, die hinterher in den Büchern gesammelt wurden.

(Nach Guareschis Tod sind nach und nach noch andere seiner Don-Camillo-und-Peppone-Erzählungen in weiteren Büchern zusammengefasst worden.)

Die Erzählungen in diesen Büchern sind allesamt sehr kurz und in sich abgeschlossen. Für die späteren Verfilmungen mussten sie daher zu zusammenhängenden Geschichten verknüpft werden.

In den Jahren 1952 bis 1963 sind Guareschis Bücher dann in den fünf Filmen 

mit

• dem überragenden Fernandel in der Rolle des Don Camillo
• und Gino Cervi in der Rolle des Giuseppe Bottazzi, genannt Peppone, verfilmt worden,

und zwar derart (neudeutsch:) "ikonisch", dass jede spätere Neuverfilmung im Vergleich damit nur noch Schrott werden kann (vgl. etwa ).

(Des weiteren gibt es ein überflüssiges Don-Camillo-Musical und diverse Theateraufführungen [u.a. voll daneben ].)

In den Filmen gibt es drei Hauptrollen:

1. der Dorfpfarrer Don Camillo,
2. der kommunistische Bürgermeister Peppone, der wie Stalin aussieht.

Beide streiten sich andauernd und sind letztlich doch beste Freunde : dieses Wechselspiel ist das Zentralthema aller fünf Filme.

3. Jesus, der üblicherweise am Kreuz über dem Altar hängt . Mit diesem Jesus liegt Don Camillo andauernd fast genauso im Clinch wie mit Peppone. Dabei ist Jesus einerseits sanft, wäscht aber andererseits Camillo auch ab und zu gründlich den Kopf. Ein Beispiel aus dem unten behandelten Film :

Don Camillo weiß sich aber auch gegen Jesus zu wehren. Als z.B. Jesus mal (in einem anderen Film) „Deine Hände sind zum Segnen da, nicht zum Prügeln“ sagt, antwortet Don Camillo frech: „Man merkt, du bist nicht von hier.“

aus dem Film ist, wie wir unten noch sehen werden, eine typische langweilige Standardaufgabe und deshalb für Schüler erstmal sicherlich völlig uninteressant.

Aber der Kontext macht's:

• Peppone, bisher Bürgermeister, möchte zum Abgeordneten im "Unterhaus" des italienischen Parlaments gewählt werden

(in ist er allerdings Senator, also Mitglied des "Oberhauses"),

muss dazu allerdings die Abschlussprüfung der Volksschule nachholen.

• Bekanntgabe der Prüfungsaufgaben:  
• Peppone hat natürlich gar nichts verstanden (worin sich wohl viele Schüler wiederfinden werden). Wichtig ist da sein letzter Satz: "Jesus Christus, hilf mir!"

• Peppone wird während der Prüfung auf den Flur gebeten, weil er (als Bürgermeister) angeblich die Einweisung eines Kranken unterschreiben muss.
• In Wirklichkeit geht es aber nicht um die Einweisung eines Kranken, sondern draußen im Flur steht Don Camillo, der Peppone helfen will (und damit - wie erbeten - Jesus?).
• Allerdings liefern die beiden sich natürlich erstmal ein kleines Scharmützel: 
• Zuguterletzt gibt Don Camillo Peppone (nicht ganz uneigennützig) die Lösung der Aufgabe:

Dass Peppone nur ganz kurz auf die (gar nicht so einfache; s.u.) Lösung schaut und sie sofort versteht, mag zwei Gründe haben:

• auf dem Blatt steht wirklich nur das Endergebnis, weil in der Prüfung nur dieses und keine Zwischenschritte erwartet werden?
• das Betrachten des Blatts ist im Film aus dramaturgischen Gründen verkürzt worden, weil ein längeres Betrachten des Blatts für den Zuschauer langweilig wäre.
• Peppones Reaktion:

("genauso gelöst" deutet aber doch den Rechenweg an).

Wenn man erstmal die Lösung hat (vorgeführt bekommt), sieht sie plötzlich ganz einfach aus.

Peppones (wenn auch unglaubwürdigen) Reaktionen könnten aber Motivation für die Schüler sein:

• Ist es wirklich "eine ganz einfache Sache"? Und wenn ja: was an der Aufgabe ist "eine ganz einfache Sache"?
• Und aus "ich hätt's genauso gelöst" folgend: wie denn?

Ich könnte mir vorstellen,

1. mit den Schülern den Film erstmal nur bis zu der Aufgabe anzuschauen,
2. dann  mit den Schülern die Aufgabe zu lösen
3. und zuguterletzt (wenn die Schüler brav mitgearbeitet haben) den restlichen Film anzuschauen.

Die Belohnung in 3. (und die Bedingung) würde ich aber schon vorher ankündigen.

Hauptteil

Im Film erscheint die Tafel mit den Aufgaben zuerst in der italienischen Originalfassung   , und dann wird kurz die deutsche Version  eingeblendet, woran uns hier nur der mathematische Teil interessiert:

(Nebenbei: der Prüfungsvorsitzende formuliert die Aufgabe ein wenig anders, als sie auf der Tafel steht.)

Aufgaben wie diese sind anscheinend international und unverwüstlich: sie kamen vor 70 Jahren in Italien vor und auch heute noch in Deutschland denkbar.

Es gibt einen guten Grund dafür: wenn man das Volumen einer Kugel durchgenommen hat und dazu eine Anwendungsaufgabe vorlegen möchte, gibt es kaum eine andere Möglichkeit als eben den Zufluss einer Flüssigkeit, weil nur diese die Kugel vollständig füllen kann.

Versuchen wir aber dennoch mal, die Aufgabe halbwegs sinnvoll zu machen:

1. gibt es tatsächlich ein annähernd halbkugelförmiges Fischbecken für den Garten zu kaufen: ;

2. will der Gartenbesitzer nun die Halbkugel mit Wasser für seine Fische füllen, aber

• verhindern, dass es überläuft und damit kostbares Wasser verschwendet wird,
• nicht die ganze Zeit danebenstehen, um den Augenblick abzuwarten, in dem das Becken komplett gefüllt ist und überläuft.

Dazu müsste er tatsächlich Überlegungen anstellen, die denen in ähneln!

Aber damit ist es auch schon vorbei mit der realistischen Anwendungsaufgabe, denn welcher Gartenbesitzer würde sowas allen Ernstes durchrechnen

(und z.B. ausmessen, wieviel Wasser in einer Minute durch den Wasserhahn bzw. Schlauch läuft)?!

Wieso aber werden Aufgaben wie dann aber doch immer wieder gestellt, statt ohne jede vorgeschobene Anwendung nur rein theoretisch zu fragen:

"Wie oft passen 6,27 Liter in eine Halbkugel mit dem Durchmesser 2,6 Meter?"
(freundliche Hilfestellung: für das Volumen einer Kugel gilt die Formel )

Für die Pseudoanwendung gibt es zwei mögliche Gründe:

• darin kann man schön bösartig die eigentliche Mathematik verstecken, damit die Schüler sie mühsam suchen und (nicht) wiederfinden

(und solches Suchen und Finden der Mathematik in Anwendungsaufgaben müssen Schüler üben!);

• auch wenn die Anwendung nur fiktiv ist, kann man sich (eine durchsichtige Salatschüssel) doch besser vorstellen als die nackte Geometrie von .

Durchaus nett an der Aufgabe ist es immerhin, dass die zwei mathematische Informationen (Zahlen und Einheiten) unterstrichen sind:

Noch netter wäre es aber, wenn des weiteren unterstrichen wären:

Aber hätten die Prüfer damit nicht schon fast alles verraten? Immerhin müssten die Schüler ja noch alles zu einer Rechnung zusammensetzen.

Halten wir aber all die unterstrichenen Informationen kurz in einer Liste fest:

1. halbkugelförmiges Gefäß,

2. Durchmesser = 2,6 Meter,

3. gefragt ist nach der Zeit, also muss man am Ende antworten: "Man braucht soundsoviel Zeit, um das halbkugelförmige Gefäß zu füllen",

4. in der Minute 6,27 Liter.

In dem Aufgabentext sind aber noch zwei weitere Informationen verborgen:

5. Meter und Liter sind zwei unterschiedliche Maßeinheiten, und bei sowas sollte man allergisch reagieren und die eine von beiden Maßeinheiten in die andere umrechnen.

6. wenn wir das Gefäß "füllen" wollen, brauchen wir dessen Volumen V.

Und drei entscheidende Informationen kommen in der Aufgabe gar nicht vor, nämlich

7. noch ziemlich einfach: dass das Volumen einer Halbkugel die Hälfte des Volumens einer ganzen Kugel ist,

8. wie man das Volumen einer ganzen Kugel berechnet, nämlich mit der Formel . Die Prüfer setzen also voraus, dass Peppone diese Formel auswendig kennt. Wie in einer Szene vorher klar wird, kannte er sehr wohl diese Formel - hat sie im Prüfungsstress allerdings vergessen?

(Ich hatte zwar ungefähre Vorstellungen von der Volumenformel [irgendwas mit Drittel, Radius hoch 3 und ], musste aber die korrekte Formel [mit der 4]  doch nochmals nachschlagen);

9. dass ein Kubikmeter (1 m³) aus 1000 Litern (1000 dm³) besteht.

Zuguterletzt: in 2. ist vom Durchmesser und in 8. vom Radius r die Rede. Wir müssen den Durchmesser d also noch in den Radius r umrechnen, und zwar mittels der Gleichung

10.  r = .

Unsere Liste sieht inzwischen also so aus:

1. halbkugelförmiges Gefäß,

2. Durchmesser = 2,6 Meter,

3. gefragt ist nach der Zeit, also muss man am Ende antworten: "Man braucht soundsoviel Zeit, um das halbkugelförmige Gefäß zu füllen",

4. in der Minute 6,27 Liter,

5. Meter und Liter sind zwei unterschiedliche Maßeinheiten, und bei sowas sollte man allergisch reagieren und die eine von beiden Maßeinheiten in die andere umrechnen,
6. wenn wir das Gefäß "füllen" wollen, brauchen wir dessen Volumen V,

7. noch ziemlich einfach: dass das Volumen einer Halbkugel die Hälfte des Volumens einer ganzen Kugel ist,

8. wie man das Volumen einer ganzen Kugel berechnet, nämlich mit der Formel . Die Prüfer setzen also voraus, dass Peppone diese Formel auswendig kennt (was bei ihm nicht der Fall ist?),

9. dass ein Kubikmeter (1 m³) aus 1000 Litern (1000 dm³) besteht.

Das sind neun (!) Zeilen, in denen teilweise mehrere Informationen stehen. Und sowas soll (wie Peppone heuchelt) "eine ganz einfache Sache" und für einen "Volksschüler" lösbar sein?!

(Dann müsste es von Gymnasiasten "mit links" erledigt werden können. Ich bezweifle aber, dass viele Gymnasiasten die Aufgabe lösen könnten.)

Durch Umsortieren der Liste (entlang des Aufgabentextes und sachlichem Zusammenhang) und Weglassen doppelter Informationen erhält man

zu A. Volumen der Halbkugel:

Oben hatte ich gesagt, in Pseudo-Anwendungsaufgaben gehe es oft darum,

"schön bösartig die eigentliche Mathematik [zu] verstecken, damit die Schüler sie mühsam suchen und (nicht) wiederfinden".

Das ist aber gleichzeitig auch ein guter Tipp:

• "Vergiss die blöde Anwendung [Füllen eines Gefäßes] und suche nach den im Aufgabentext versteckten rein mathematischen Inhalten."

• Insbesondere geht es immer darum, Gleichungen aufzustellen (und dann zu lösen).

Inzwischen haben wir aber schon die beiden Gleichungen r = und .

Der nächste gute Tipp ist dann:

• "Suche eine Gleichung, in der nur noch eine einzige Unbekannte vorkommt, alles andere aber bereits bekannt ist (also eine Gleichung, die sich [hoffentlich] lösen lässt)."

Das ist in der Gleichung r = der Fall:

• der Radius r ist noch unbekannt,

• aber wir wissen schon, dass d = 2,6 m ist.

Damit erhalten wir

r = = = 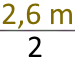1,3 m

bzw. kurz

r =                              1,3 m

Damit ist nun aber auch in der anderen Gleichung alles (außer V) bekannt

(wenn wir wissen, dass hinter dem Symbol eine Zahl steckt, nämlich ungefähr 3,14).

Durch Einsetzen erhalten wir

bzw. kurz

V  ≈        9,16            m ³ .

Das ist das Volumen der ganzen Kugel. Also erhalten wir mit 4. das Volumen der Halbkugel als

bzw. kurz

.

zu B. Zwischenschritt:

Weil

• in Kubikmetern (m³) gemessen wird
• die zufließende Wassermenge jedoch in Litern,

 müssen wir uns kurz an

5. eine von beiden Maßeinheiten in die andere umrechnen: ein Kubikmeter besteht aus 1000 Litern

erinnern:

= 1000 • 4,58 Liter  = 4580 Liter 

bzw. kurz

                                                                        4580 l

Zu C. zufließendes Wasser:

wie oft passen nun 6,27 Liter in 4580 Liter?:

4580 : 6,27 730

6,27 Liter passen also ungefähr 730 mal in 4580 Liter.

Und damit sind wir entsprechend

7. "Man braucht                 soundsoviel    Zeit    , um das halbkugelförmige Gefäß zu füllen"

endlich am Ziel:

     "Man braucht ungefähr        730        Minuten, um das halbkugelförmige Gefäß zu füllen."

(... was man noch der Anschaulichkeit zuliebe in 730  : 60 ≈  12 Stunden umrechnen könnte: so lange kann unser Fischteichbesitzer also Besseres tun, als stumpf zuzuschauen, wie der Teich sich füllt, zumal der Wasserspiegel wegen der Halbkugelform des Teichs anfangs schnell, danach aber immer langsamer steigt; man kann so ein 12 Stunden langes Zuschauen allerdings auch meditativ finden: ; dabei ist das Auffangbecken unten zwar keine Halbkugel, aber immerhin doch ein "Kugelsegment": ).

Insgesamt erfolgt die Lösung also in nur fünf Schritten:

1. r   =   1,3 m ,
2. V  ≈   9,16 m ³ ,
3. ,
4.    4580 l ,
5.         4580 : 6,27 730 .

(Die einzige umständliche Zwischenrechnung ist

Mal abgesehen von notwendigen einfachen "Termumformungen" dürfte das im Zeitalter des Taschenrechners kein Problem mehr sein - während Peppone all das noch schriftlich rechnen musste!)

Wie so oft im Mathematikunterricht

(und insbesondere bei Textaufgaben)

besteht die Schwierigkeit also

• nicht (wie fälschlich ankündigt) im Rechnen (vgl. ),
• sondern im Zusammentragen der mathematischen Informationen in der Aufgabenstellung, also

Solches Erfassen aller mathematischen Informationen ist aber erheblich schwieriger, als die meisten Mathematiklehrer es sich vorstellen.