Heiner Stauff - anschauliche Mathematik

wie ich vor lauter Ungeduld das

"Gesetz der [riesig] großen Zahlen"
gründlich falsch verstanden habe

Ich mache hier nicht mal einen Unterschied zwischen "schwachem" und "starkem" "Gesetz der großen Zahlen", sondern entnehme Wikipedia die landläufige Definition:

"Gesetz der großen Zahlen ist eine Bezeichnung für bestimmte mathematische Sätze

[Plural!; und gemeint damit sind eben das "schwache" und das "starke" Gesetz]

[...]. In ihrer einfachsten Form besagen diese Sätze, dass die relative Häufigkeit eines Zufallsergebnisses [...] gegen die Wahrscheinlichkeit des Zufallsergebnisses konvergiert, wenn das Zufallsexperiment immer wieder durchgeführt wird."
(Quelle: )

Obwohl schon relativ einfach ausgedrückt, wird das einem Laien dennoch wahrscheinlich (!) wegen der ungeklärten Begriffe "Häufigkeit eines Zufallsereignisses"/"Wahrscheinlichkeit des Zufallsereignisses" unverständlich bleiben.

Man kann das natürlich - wie eben Wikipedia - so

"Die Wahrscheinlichkeit, dass eine Münze beim Werfen Kopf zeigt, betrage ¹/₂. Je häufiger die Münze geworfen wird, desto unwahrscheinlicher ist es dann, dass der Anteil der Würfe, bei denen Kopf erscheint, um mehr als ein beliebig vorgegebenes ε > 0 vom theoretischen Wert ¹/₂ abweicht. Demgegenüber ist durchaus wahrscheinlich, dass die absolute Differenz zwischen der Anzahl der Kopf-Würfe und der halben Gesamtzahl der Würfe anwächst."

oder gar so

"Schwaches Gesetz der großen Zahlen

Man sagt, eine Folge von Zufallsvariablen 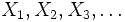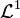$X_1, X_2, X_3, \dots$ in $\mathcal{L}^1$ genüge dem schwachen Gesetz der großen Zahlen, wenn für 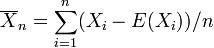$\overline{X}_n=\sum_{i=1}^{n}(X_i-E ( {X}_i ))/n$ für alle positiven Zahlen $\varepsilon$ gilt:

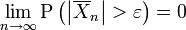$\lim_{n\rightarrow\infty}\operatorname{P}\left(\left|\overline{X}_n\right|>\varepsilon\right)=0$ .

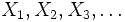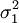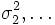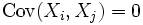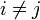Es gibt verschiedene Voraussetzungen, unter denen das schwache Gesetz der großen Zahlen gilt. Es gilt beispielsweise, wenn die Zufallsvariablen $X_1, X_2, X_3, \dots$ endliche Varianzen $\sigma_1^2$ , $\sigma_2^2,\dots$ besitzen, die zudem durch eine gemeinsame obere Grenze beschränkt sind, und jeweils paarweise unkorreliert sind, also $\operatorname{Cov}(X_i, X_j) = 0$ for $i\neq j$ erfüllen.

Das schwache Gesetz der großen Zahlen von Chintschin nennt als Bedingung für die stochastische Konvergenz, dass die Zufallsvariablen einer Folge 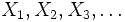$X_1, X_2, X_3, \dots$ unabhängig und identisch verteilt sind und einen endlichen Erwartungswert besitzen.

Der Beweis der genannten Sätze lässt sich jeweils über die Tschebyschow-Ungleichung führen.

Starkes Gesetz der großen Zahlen

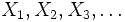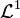Man sagt, eine Folge von Zufallsvariablen $X_1, X_2, X_3, \dots$ in $\mathcal{L}^1$ genüge dem starken Gesetz der großen Zahlen, wenn für 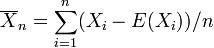$\overline{X}_n=\sum_{i=1}^{n}(X_i-E ( {X}_i ))/n$ gilt:

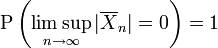$\operatorname{P}\left(\limsup_{n\rightarrow\infty}|\overline{X}_n|=0\right)=1$ .

Das starke Gesetz der großen Zahlen impliziert das schwache Gesetz der großen Zahlen.

Ein starkes Gesetz der großen Zahlen gilt beispielsweise, wenn die Folge unabhängig ist und die Zufallsvariablen identisch verteilt sind. Eine Form des starken Gesetzes der großen Zahlen für abhängige Zufallsvariablen ist der Ergodensatz."

erklären, aber das ist für einen Laien

(für den das allerdings auch gar nicht geschrieben ist)

sicherlich vollends unverständlich, ja, es verbaut ihm geradezu den Zugang zur anschaulichen Quintessenz des "Gesetzes der großen Zahlen".

Machen wir es also an einem ersten Beispiel anschaulich:

angenommen, wir haben einen tatsächlich oder scheinbar "fairen" Spielwürfel , dessen Seiten alle mit derselben Wahrscheinlichkeit ¹/₆ fallen.

Nun würfeln wir fünf mal nacheinander und erhalten z.B. die Reihenfolge 2, 2, 2, 2, 2, also fünf mal die 2.

Die sogenannte "relative Häufigkeit" des Zufallsereignisses "2, 2, 2, 2, 2" ist

"1" heißt in der Wahrscheinlichkeitsrechnung aber "absolut sicher", und in der Tat ist es ja höchst merkwürdig, dass in sämtlichen bisherigen Würfen ausschließlich die 2 erschienen ist.

Da zweifelt man doch langsam daran, dass der äußerlich "fair" aussehende Würfel auch wirklich "fair" ist. Könnte nicht ein geheimer Mechanismus (???) eingebaut sein, dass der Würfel wenn schon nicht mit Sicherheit, so doch mit erhöhter Wahrscheinlichkeit das Ergebnis 2 zeigt?

Und schon haben wir das erste Problem:

einerseits könnte der Würfel tatsächlich gezinkt sein,
andererseits ist aber bei einem "fairen" Würfel das Zufallsereignis "2, 2, 2, 2, 2" genauso wahrscheinlich wie z.B. "1, 3, 6, 4, 4", nur dass uns klare Muster wie eben "2, 2, 2, 2, 2" oder z.B. auch "1, 6, 1, 6, 1" viel eher auffallen und wir bei solchen Mustern wohl fast versucht sind, Absicht

(des Würfels, der Vorsehung, ?)

zu unterstellen.

Kommen wir damit aber zum nächsten, also sechsten Wurf:

falls der Würfel gezinkt ist

(wofür nach dem Anfang "2, 2, 2, 2, 2" ja einiges spricht!),

werden wir vermuten, dass mit hoher Wahrscheinlichkeit wieder eine 2 fällt;

falls der Würfel nicht gezinkt, also "fair" ist, neigen wir hingegen dazu, für den sechsten Wurf nun endlich das Ende der 2er-Serie zu erwarten, also eine der Zahlen 1, 3, 4, 5, 6. Wir erwarten also das Ende des Musters und somit das Ende der Absicht. Das aber heißt, dass die Zahlen 1, 3, 4, 5, 6 nun mit erhöhter Wahrscheinlichkeit erscheinen, die 2 aber mit verringerter Wahrscheinlichkeit.

Und damit unterstellen wir, dass der Würfel

(oder die Vorsehung, ?)

ein Gedächtnis hat, nämlich weiß, dass er bislang allzu oft die 2 gezeigt hat und deshalb nun mal eine andere Zahl folgen lassen muss.

Mit solchen Gedanken sind wir schon sehr nah am

(allerdings nur halb verstandenen)

"Gesetz der großen Zahlen": wir verlassen uns intuitiv darauf, dass der Würfel, wenn er denn "fair" ist, die Zahlen 1, 2, 3, 4, 5, 6 auf die Dauer gleich oft zeigen wird.

Die Halbwahrheit besteht allerdings darin zu meinen, weil die 2 bislang so oft erschienen ist, müsse sie im nächsten Wurf seltener erscheinen. Nein, falls der Würfel tatsächlich "fair" ist, erscheint sie im sechsten Wurf mit derselben Wahrscheinlichkeit ¹/₆ wie die anderen Zahlen 1, 3, 4, 5, 6. Das aber bedeutet:

die 2 kann tatsächlich nochmals erscheinen, und zwar wieder mit der Wahrscheinlichkeit ¹/₆;
mit derselben Wahrscheinlichkeit ¹/₆ erscheinen aber auch die anderen fünf Zahlen 1, 3, 4, 5, 6;
zusammen genommen heißt das aber, dass mit der Wahrscheinlichkeit ⁵/₆ nicht mehr die 2 erscheint, sondern eine andere Zahl (also entweder 1 oder 3 oder 4 oder 5 oder 6);

es ist also auch ohne irgendeine "Absicht" zwar möglich, aber doch eher unwahrscheinlich, dass im sechsten Wurf nochmals die 2 erscheint;
der Würfel hat also ohne jede "Absicht" und ohne jedes "Gedächtnis" die Tendenz, vorherige einseitige Ergebnisse auszugleichen.

"Wenn die Unterrichtsstunde [und schon die Unterrichtsvorbereitung] nicht damit endet, dass der Lehrer [keineswegs nur pädagogisch, sondern durchaus auch fachlich] etwas gelernt hat, weiß er nicht, wie man lehrt."
(John Archibald Wheeler)

Aber ich schreibe meine Essays (und insbesondere diesen) ja nicht (nur), um anderen Leuten (SchülerInneN) Mathematik beizubringen, also ihnen nur (immerhin möglichst anschaulich) von oben herab zu vermitteln, was ich selbst längst weiß.

Sondern oftmals (und insbesondere hier) lerne ich ja selbst in Essays dazu bzw. schreibe ich über etwas, was ich selbst auch lange Zeit nicht oder falsch verstanden habe.

Ich hatte das "Gesetz der großen Zahlen" bislang auch immer halbrichtig verstanden, nämlich gemeint

(obwohl ich ja wusste, dass das nicht sein kann),

dass der Würfel paradoxerweise eben doch eine Art "Gedächtnis" haben muss, um frühere einseitige Ergebnisse (2, 2, 2, 2, 2) auszugleichen.

(Und ich hatte - horribile dictu - solche halbwahren Überlegungen sogar als "Philosophie" ausgegeben.)

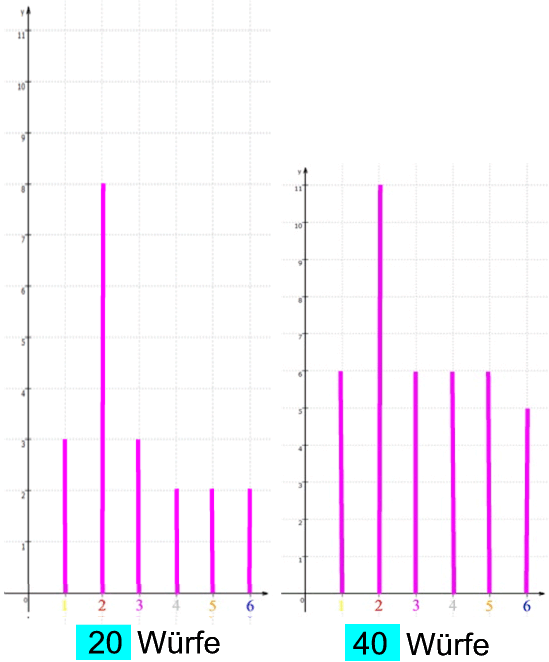
Nehmen wir nur mal das Beispiel, dass nach dem Anfang "2, 2, 2, 2, 2" noch 15 mal, also insgesamt 20 mal gewürfelt wird. Dann muss doch in den 15 weiteren Würfen die 2 erheblich seltener als die Zahlen 1, 3, 4, 5, 6 vorkommen, damit in den 20 Würfen alle Zahlen (also die 2 ebenso wie 1, 3, 4, 5, 6) etwa gleich oft vorkommen!? Der Würfel muss also sozusagen auf eine "2er-Diät" gehen!?

"Wenn man vom Rathaus kommt, ist man [natürlich!] schlauer": im Nachhinein ist mir sonnenklar, worin mein Denkfehler bestand: ich hatte die "großen" Zahlen im "Gesetz der großen Zahlen" nicht riesig genug gedacht, sondern war zu ungeduldig, wollte nämlich bereits bei "nur" 20 Würfen einen Ausgleich der relativen Häufigkeiten sehen.

(Und wie so oft, so ist es mir auch hier im Nachhinein fast unverständlich, wie ich vorher so falsch denken konnte.)

Nehmen wir also mal an, der Würfel sei tatsächlich "fair" und nach den ersten fünf Würfen "2, 2, 2, 2, 2" folgten nun alle Zahlen (also die 2 genauso wie 1, 3, 4, 5, 6) mit derselben Wahrscheinlichkeit. Der Einfachheit halber stellen wir uns dabei vor, sie folgten auch der Größe nach, also

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

2, 2, 2, 2, 2, 1, 2, 3, 4, 5, 6, 1, 2, 3, 4, 5, 6, 1, 2, 3

(wichtig an diesem Konstruktionsschema ist allein, dass die neuen Zahlen nicht die mindeste Rücksicht darauf nehmen, dass vorher schon so viele 2en da waren).

Damit erscheint

die 1 drei mal, also mit der relativen Häufigkeit ³/₂₀,
die 2 acht mal, also mit der relativen Häufigkeit ⁸/₂₀,
die 3 drei mal, also mit der relativen Häufigkeit ³/₂₀,
die 4 zwei mal, also mit der relativen Häufigkeit ²/₂₀,
die 5 zwei mal, also mit der relativen Häufigkeit ²/₂₀,
die 6 zwei mal, also mit der relativen Häufigkeit ²/_20.

Grafisch dargestellt:

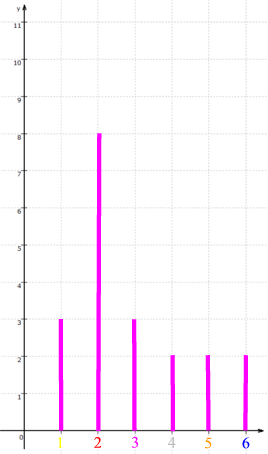
Damit

hat zwar die 2 noch immer die höchste relative Häufigkeit, nämlich ⁸/₂₀

(während die anderen Einzelzahlen 1, 3, 4, 5, 6 geringere relative Häufigkeiten zwischen ²/₂₀ und ³/₂₀ haben),

aber die anderen Zahlen 1, 3, 4, 5, 6 zusammen tauchen schon häufiger als die 2 auf, nämlich insgesamt mit der relativen Häufigkeit ¹²/₂₀ ; die anderen Zahlen 1, 3, 4, 5, 6 holen also immerhin schon auf!

Dieser Trend wird noch deutlicher, wenn wir mal von 40 Würfen (nach derselben Regel) ausgehen:

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

2, 2, 2, 2, 2, 1, 2, 3, 4, 5, 6, 1, 2, 3, 4, 5, 6, 1, 2, 3

21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40

4, 5, 6, 1, 2, 3, 4, 5, 6, 1, 2, 3, 4, 5, 6,, 1, 2, 3, 4, 5

Nun erscheint

die 1 sechs mal, also mit der relativen Häufigkeit ⁶/₄₀,
die 2 elf mal, also mit der relativen Häufigkeit ¹¹/₄₀,
die 3 sechs mal, also mit der relativen Häufigkeit ⁶/₄₀,
die 4 sechs mal, also mit der relativen Häufigkeit ⁶/₄₀,
die 5 sechs mal, also mit der relativen Häufigkeit ⁶/₄₀,
die 6 fünf mal, also mit der relativen Häufigkeit ⁵/_40.

Graphisch dargestellt:

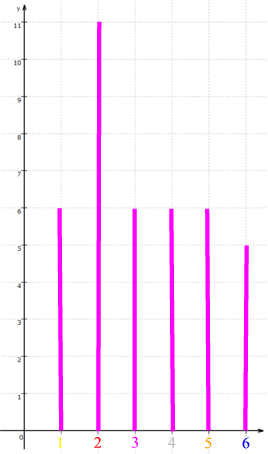
Wie nicht anders zu erwarten, taucht also die 2 nach wie vor am häufigsten auf, aber doch nur noch in ca. ¹/₄ der Fälle.

Und jetzt endlich kann man sehen, wie es wirklich läuft: zwar wird die relative Häufigkeit der 2

bei unserem Schema in alle Ewigkeit am größten bleiben,
aber sich doch immer mehr (von oben) der Zahl ¹/₆ annähern.

Und nach unserem Schema wird die relative Häufigkeit der anderen Zahlen 1, 3, 4, 5, 6

zwar immer jeweils unterhalb von ¹/₆ liegen,
aber sich doch immer mehr (von unten) der Zahl ¹/₆ annähern.

Insgesamt nähern/t sich also

sowohl die relative Häufigkeit der 2
als auch die relative Häufigkeit von 1, 3, 4, 5, 6

der Zahl ¹/₆ an.

Anders gesagt: wenn häufig genug gewürfelt wird, fällt es kaum mehr ins Gewicht, dass die 2 anfangs läppische fünf mal nacheinander vorkam.

Das Aufholen der Zahlen 1, 3, 4, 5, 6 von 20 zu 40 Würfen wird nebenbei besonders schön deutlich, wenn man die beiden obigen Grafiken "normiert", indem man die beiden höchsten, also die 2er-Werte gleich hoch macht:

Damit aber zurück zu dem Problem, dass wir uns ja gar nicht sicher sein können, ob der Würfel "fair" ist. Schließlich kann man es einem Würfel nicht auf Anhieb ansehen/anfühlen, ob er "fair" ist. Genau genommen

können wir uns sogar nie sicher sein, ob ein Würfel vollends "fair" ist,
d.h. die "wahre" Wahrscheinlichkeit, mit der (falls üüberhaupt alle vorhanden) die Zahlen 1, 2, 3, 4, 5, 6 auftauchen, ist uns prinzipiell nicht zugänglich.

Das aber heißt doch, dass wir sie üüberhaupt erst durch "das Gesetz der großen Zahlen" erschließen, d.h. durch vielfaches Würfeln herausbekommen können.

(Das aber heißt für mich: die relative Häufigkeit konvergiert nicht gegen eine a priori vorgegebene Wahrscheinlichkeit, sondern die Wahrscheinlichkeit ist üüberhaupt erst definierbar als der Grenzwert der relativen Häufigkeiten. Die Wahrscheinlichkeit eines Ereignisses steht also nicht am Anfang, sondern am Ende. Vgl. )

Nun gibt es allerdings einen radikalen Unterschied zwischen alltäglichem (Spiel-) und mathematischem Würfeln:

einerseits sind die industriell gefertigten Würfel derart perfekt, dass sie (annähernd) "fair" sind,
andererseits werden aber diese Würfel im mikroskopischen Bereich dennoch Abweichungen von der perfekten Glattheit und Symmetrie haben, also leicht "unfair" sein.
Diese minimalen Ungenauigkeiten sind aber z.B. bei völlig irrelevant: da wird man den Teufel tun, den Würfel vor dem Spiel ausgiebig zu "problematisieren", sondern man benutzt ihn ohne großartiges Nachdenken als a priori faires "Handwerkszeug"

(und verzweifelt dennoch ab und zu an seiner vermeintlichen Willkür, die fast als bösartige Absicht oder mehr oder minder gerechte "Strafe des Schicksals" empfunden wird, ärgert sich also eben doch [über ihn]).

D.h. beim Alltagsgebrauch von Würfeln interessieren überhaupt nicht die wirklich interessanten mathematischen Probleme.

In der Mathematik ist es nämlich just umgekehrt: ein von vornherein verlässlich "fairer" Würfel

(wie er eben [leider!] noch meistens im Unterricht durchgenommen wird; vgl. )

ist mathematisch weitgehend uninteressant: bei ihm ist bereits alles bekannt, gibt es also nichts mehr zu entdecken. Sondern viel interessanter sind mehr oder minder offensichtlich "unfaire" Würfel, deren "wahre" Wahrscheinlichkeit üüberhaupt erst durch das "Gesetz der großen Zahlen" ermittelt werden kann.

(Ein Problem ist allerdings, dass es solche offensichtlich oder verborgen "unfairen" Würfel kaum zu kaufen gibt. Da nehme man sich halt selbstmodellierte Würfel oder Lego®steine.

Mit solchen "unfairen" Würfeln lassen sich aber durchaus interessante Spiele entwickeln. Weil die Wahrscheinlichkeit der einzelnen Seiten unbekannt ist, muss man sie erst mal mit dem "Gesetz der großen Zahlen", also durch vielfaches Würfeln ermitteln und dann für die verschiedenen Seiten verschiedene Einsätze aufstellen.)

Bemerkenswert ist nun, dass das "Gesetz der großen Zahlen" genauso wie für "faire" auch für "unfaire" Würfel gilt, also auch bei einem "unfairen" Würfel die Wahrscheinlichkeit der Einzelseiten durch vielfaches Würfeln ermittelt werden kann.

Auch dazu ein Beispiel:

angenommen wieder mal, die erste fünf Würfe ergäben allesamt 2en, wir erhielten also wieder die Reihenfolge 2, 2, 2, 2, 2;
jetzt gehen wir mit guten Gründen aber mal davon aus, dass der Würfel tatsächlich "unfair" ist und unterstellen beispielsweise, dass die 2 zwar nicht immer fällt, aber doch mit der erhöhten Wahrscheinlichkeit ¹/₂, also in der Hälfte aller Fälle;
dazu konstruieren wir die neue Reihenfolge 2, 2, 2, 2, 2, 1, 3, 4, 5, 6, 2, 2, 2, 2, 2, 1, 3, 4, 5, 6 ... von der wir aber nur die ersten zehn Würfe 2, 2, 2, 2, 2, 1, 3, 4, 5, 6 betrachten

(wichtig an diesem neuen Konstruktionsprinzip ist nebenbei nicht, dass die 2 fünf mal hintereinander auftritt, sondern allein, dass sie innerhalb einer "Periode" in der Hälfte aller Fälle vorkommt; denkbar wäre also beispielsweise auch 2, 2, 2, 2, 2, 1, 2, 3, 2, 4, 2, 5, 2, 6 , 1, 2, 3, 2, 4, 2, 5, 2, 6 ...);

Dabei erscheint

die 1 ein mal, also mit der relativen Häufigkeit ¹/₁₀,
die 2 fünf mal, also mit der relativen Häufigkeit ⁵/₁₀,
die 3 ein mal, also mit der relativen Häufigkeit ¹/₁₀,
die 4 ein mal, also mit der relativen Häufigkeit ¹/₁₀,
die 5 ein mal, also mit der relativen Häufigkeit ¹/₁₀,
die 6 ein mal, also mit der relativen Häufigkeit ¹/₁₀,

d.h. die 2 hat bereits jetzt die relative Häufigkeit ¹/2, die mit ihrer Wahrscheinlichkeit überein stimmt.

Kommen wir damit aber zurück zur Wikipedia-Definition

Nun kann es aber durchaus passieren, dass man beispielsweise mit einem durchaus "fairen" Würfel andauernd und in alle Ewigkeit 2en würfelt

(was zwar höchst unwahrscheinlich, aber eben doch nicht ausgeschlossen ist).

Obwohl der Würfel "fair", die Wahrscheinlichkeit des Zufallsergebnisses 2 also ¹/₆ ist, ergäbe sich für die relative Häufigkeit des Zufallsergebnisses 2 also 1, d.h. die relative Häufigkeit würde nicht gegen die "echte" Wahrscheinlichkeit konvergieren.

Man kann sich also nie vollends sicher sein, dass man durch häufiges Würfeln die reale Wahrscheinlichkeit eines Ereignisses ermittelt.

für mein (begrenztes?) Verständnis heißt das aber: das "Gesetz der großen Zahlen"

ist einerseits eine Aussage über Wahrscheinlichkeiten,
gilt andererseits aber selbst nur mit einer gewissen (wenn auch sehr großen) Wahrscheinlichkeit.

Bzw. doppelt gemoppelt: je länger man würfelt, mit desto größer
er Wahrscheinlichkeit ermittelt man die Wahrscheinlichkeit eines Ereignisses

(falls die Wahrscheinlichkeit des Ereignisses nicht überhaupt erst aus dem langen Würfeln geschlossen wird).

Zuguterletzt: ich hätte frühzeitig den Wikipedia-Artikel lesen sollen, denn darin steht auch:

"Das Gesetz der großen Zahlen bedeutet [...] nicht, dass ein Ereignis, welches bislang nicht so häufig eintrat wie erwartet, seinen „Rückstand“ irgendwann ausgleichen und folglich in Zukunft häufiger eintreten muss. Dies ist ein bei Roulette- und Lottospielern häufig verbreiteter Irrtum, die „säumige“ Zahlenart müsse nun aber aufholen, um wieder der statistischen Gleichverteilung zu entsprechen."

... was immerhin beweist, dass mein Denkfehler gängig ist.