zuerst beseitigen, was am weitesten vom nackten
 entfernt ist
entfernt istGleichungen lösen:
zuerst beseitigen, was am
weitesten vom nackten
 entfernt ist
entfernt ist
"Man muss die Dinge so einfach wie
möglich machen.
Aber nicht einfacher."
(Albert Einstein)
 ,
,


In der Mathematik ist es genauso: bei Gleichungen interessiert vor allem 1 • x = x , wofür im Folgenden oft als Symbolbild der nackte David von Michelangelo benutzt wird:

Der einzige Unterschied
zwischen Mathematik und Alltagsleben ist, dass es
in der Mathematik beim Lösen von Gleichungen manchmal mehrere Lösungen für ![]() gibt
gibt
![]() - 4 =
0
- 4 =
0
Schauen wir uns zuerst nur die linke Seite der
Gleichung an, also
![]() - 4 :
- 4 :
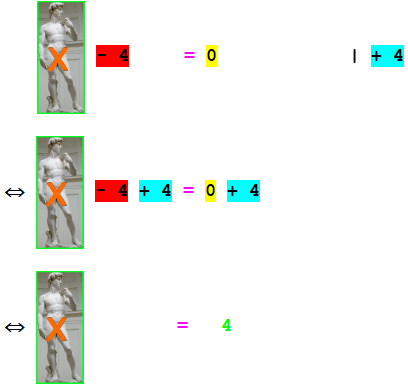
Halten wir noch fest:
Das Lösen von Gleichungen sieht immer so aus: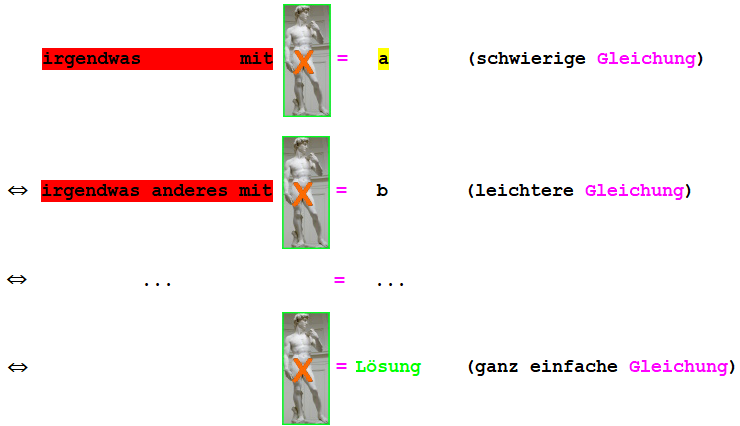 |
||
|
Ziel ist es immer, dass am Ende der Rechnung
|
 Nie alles auf einmal machen!)
Nie alles auf einmal machen!)| „Immer vom x aus rechnen!“ |
 Diese zufällig gewählte Zahl
3 ist
Diese zufällig gewählte Zahl
3 ist : die zufällig gewählte Zahl
3 war also NICHT die Lösung der Anfangsgleichung
2•x
- 8 =
4
, denn wir haben auf der linken
Gleichungsseite NICHT
4, sondern
-2
erhalten;
: die zufällig gewählte Zahl
3 war also NICHT die Lösung der Anfangsgleichung
2•x
- 8 =
4
, denn wir haben auf der linken
Gleichungsseite NICHT
4, sondern
-2
erhalten;Beim Lösen von
2•
![]() -8 =
4
gehen wir nun genau umgekehrt vor und
beseitigen zuerst die zweite, von
-8 =
4
gehen wir nun genau umgekehrt vor und
beseitigen zuerst die zweite, von
![]() „entferntere“ Rechnung
-8 :
„entferntere“ Rechnung
-8 :
2•
![]() -8 =
4
| +8
-8 =
4
| +8
⇔
2•
![]() -8
+8 =
4
+8
-8
+8 =
4
+8
⇔
2•
![]() = 12
= 12
Beim Lösen von Gleichungen gilt also die Faustregel:
|
zuerst beseitigen, was am
weitesten vom nackten
|
Und jetzt erst können wir auf der linken Gleichungsseite auch noch die erste, „nähere“ Rechnung 2• beseitigen:
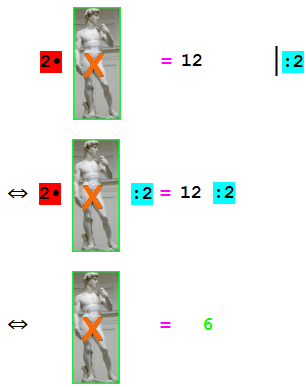
ein schwieriges Beispiel:
3• ( x -4 )2 -75 = 0
3• (
![]() -4 )2 -75 = 0
-4 )2 -75 = 0
(Anderweitig ist durchaus
wichtig, was uns hier nicht interessieren soll:
Ziel ist es wie immer auch hier wieder, das nackte
![]() zu berechnen.
zu berechnen.
Schauen wir uns dazu die linke Seite der
Gleichung genauer an, also
3• ( ![]() -4 )2 -75 .
-4 )2 -75 .
Was (außer ![]() ) stört da? Doch offensichtlich alles andere,
nun rot Markierte:
) stört da? Doch offensichtlich alles andere,
nun rot Markierte:
3•
( ![]() -4 )2
-75 .
-4 )2
-75 .
All dieses rot Markierte
muss auf die Dauer auf der linken Gleichungsseite
verschwinden, so dass da nur noch das nackte
![]() übrigbleibt.
übrigbleibt.
Damit stellt sich aber die Frage, in welcher Reihenfolge wir die verschiedenen rot markierten Details auf der linken Gleichungsseite verschwinden lassen müssen
(womit unterstellt wird, dass die Reihenfolge nicht beliebig ist).
Um die einzig richtige Reihenfolge herauszufinden, setzen wir in 3• ( x -4 )2 -75 für x probeweise eine zufällig gewählte Zahl ein, also z.B. 6 , und erhalten
3• ( 6 -4 )2 -75 .
 Die zufällig gewählte Zahl
6 ist
Die zufällig gewählte Zahl
6 istDa in 3• ( 6 -4 )2 -75 keine Unbekannte mehr vorkommt, können wir es komplett ausrechnen. Dabei beginnen wir ausgehend von der 6 :
6 -4 = 2
( 2 )2 = 4
3• 4 = 12
12 -75 = -63
 : die zufällig gewählte Zahl
6 war also NICHT die Lösung der Anfangsgleichung
3• (
x
-4 )2 -75
= 0 , denn wir haben auf der
linken
Gleichungsseite NICHT 0, sondern
-63
erhalten;
: die zufällig gewählte Zahl
6 war also NICHT die Lösung der Anfangsgleichung
3• (
x
-4 )2 -75
= 0 , denn wir haben auf der
linken
Gleichungsseite NICHT 0, sondern
-63
erhalten;Fassen wir nun die Reihenfolge der Rechenschritte kurz zusammen:
Nach der Faustregel
|
zuerst beseitigen, was am
weitesten vom nackten
|
beseitigen wir nun die einzelnen Rechnungen im umgekehrter Reihenfolge, also
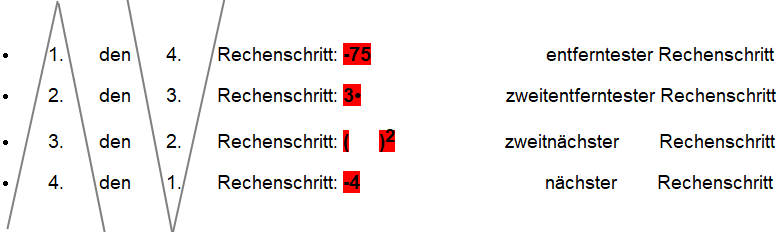
Die Rechnung sieht dann so aus:
3•
( ![]() -4 )2
-75
= 0
| +75
-4 )2
-75
= 0
| +75
⇔
3•
( ![]() -4 )2
-75 +75
= 0
+75
-4 )2
-75 +75
= 0
+75
⇔
3•
( ![]() -4 )2
=
75
| :3
-4 )2
=
75
| :3
⇔
3•
( ![]() -4 )2
:3 =
75 :3
-4 )2
:3 =
75 :3
⇔
( ![]() -4 )2
=
25
|
-4 )2
=
25
| ![]()
⇔
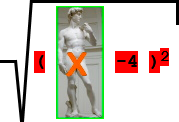 =
=
![]()
![]()
⇔
![]() -4
=
-4
=
![]() 5
| +4
5
| +4
⇔
+4
![]() -4
=
+4
-4
=
+4
![]() 5
5
⇔
![]() =
+4
=
+4
![]() 5
5
⇔
![]() =
+4 +
5 oder
=
+4 +
5 oder
![]() = +4
- 5
= +4
- 5
⇔
![]() =
9 oder
=
9 oder
![]() =
-1
=
-1
Obwohl wir immer nach dem nackten
![]() gesucht haben, hat sich
gesucht haben, hat sich ![]() am Ende als Zwillinge herausgestellt:
am Ende als Zwillinge herausgestellt:
