
| eine Lampe |
Anschauung / Anwendung
oder
 |
für die Mathematik |
... auf dass den Mathematikern ein Licht aufgehe
|
In meine Essays zum Thema
 habe ich
mehrfach Überlegungen zum Unterschied "Anschauung / Anwendung" eingestreut.
habe ich
mehrfach Überlegungen zum Unterschied "Anschauung / Anwendung" eingestreut.
Zwei Beispiele:
| Vielleicht sind sogar die vielgeschmähten "eingekleideten" (Pseudo-)Anwendungsaufgaben viel besser als ihr Ruf, nämlich in Wirklichkeit beste Veranschaulichungsaufgaben, bei denen beispielsweise eine technische Anwendung "nur" dazu dient, Innermathematisches besser zu verstehen (und nicht umgekehrt die Mathematik dazu, eine bessere Technik zu erhalten) [...]: die ganze Welt [...] ist geeignet, wenn nicht geradezu dazu geschaffen, die Mathematik zu veranschaulichen. |
|
Ein konkretes Beispiel für
ist die Lampe
 , die letztens über einem Tisch in einem Restaurant schwebte, in dem
meine Gemahlin und ich gespiesen haben.
, die letztens über einem Tisch in einem Restaurant schwebte, in dem
meine Gemahlin und ich gespiesen haben.
Bekanntlich lässt sich über Geschmack nicht streiten
(bzw. für den [ein-]gebildeten Lateiner "De gustibus non est disputandum"),
und eigentlich will ich den Besitzern des ansonsten exzellenten Restaurants auch nicht zu nahe treten."Wenn Design ist, muss man [...] sagen: »Die Lampen leiden am meisten darunter.«"
In
Lampenläden
wird mir durch all die dort ausgestellten Geschmacklosigkeiten immer ganz trostlos zumute, und dann wünsche ich mir, dass
(wie auch in Einrichtungs-Läden für die armen
![]() sowie dezent
protzenden reichen Leute
sowie dezent
protzenden reichen Leute
![]() )
)
ein Bulldozer all den
 -Wohlstandsmüll
in einen Müllcontainer schiebt
-Wohlstandsmüll
in einen Müllcontainer schiebt
(
: "Und am
Mittwoch kommt die Müllabfuhr und holt den ganzen Plunder")
oder (besser noch) die Lampen-Fabriken ihren Krempel ohne Umweg über die Kunden direkt auf den Müllplatz fahren.
Die Lampe
 erfüllt
ihren gänzlich unmathematischen
Zweck, den darunter stehenden Tisch auszuleuchten, aber
erfüllt
ihren gänzlich unmathematischen
Zweck, den darunter stehenden Tisch auszuleuchten, aber
 ausreichen (?)
ausreichen (?)
 unnötig .
unnötig . Nun interessiert mich hier aber
 , also die
eigentliche Lampe,
, also die
eigentliche Lampe, "unten rum":
"unten rum":
(Der Fairness halber sei hier aber kurz
ein- und dann dennoch der Mathematik zuliebe schleunigst wieder beiseite
geschoben, dass
 vielleicht
vielleicht
 ,
, gleichmäßig[er]
auf den darunter stehenden Tisch zu verteilen
gleichmäßig[er]
auf den darunter stehenden Tisch zu verteilen
[
 als moderne Variante von
als moderne Variante von
 ?].)
?].)
Aber zurück dazu, dass "das Gedöns
 [...] überhaupt erst
und nur mathematisch »Sinn macht«".
[...] überhaupt erst
und nur mathematisch »Sinn macht«".
Damit möchte ich allerdings nicht behaupten,
dass der Designer, der die Lampe
 verbrochen hat
verbrochen hat
Wie so oft in der Wissenschaft:
"[...] [nur] wer da [schon] hat,
dem wird gegeben werden [...]"
(Matthäus-Evangeliums
25,29)
(aber noch nicht betriebsblind ist);
 :
das Neue, um das es mir hier geht, kann nur erkennen, wer
:
das Neue, um das es mir hier geht, kann nur erkennen, wer 
 kennt
kennt (oder gar wie ich schon eines
gebaut hat:
 ; vgl.
; vgl. ![]()
 ).
).
Weil ich aber derart vorbelastet bin,
dachte ich, als ich mich dem Tisch näherte und die Lampe deshalb erstmal
zweidimensional von vorne sah
 , an das dreieckige
Oberteil
, an das dreieckige
Oberteil
 des
Galtonbretts.
des
Galtonbretts.
Und die Glaskugeln erinnerten mich an
fallende Regentropfen
 und
diese wiederum an die Kugeln, die im Galtonbrett hinunter rieseln:
und
diese wiederum an die Kugeln, die im Galtonbrett hinunter rieseln:
 .
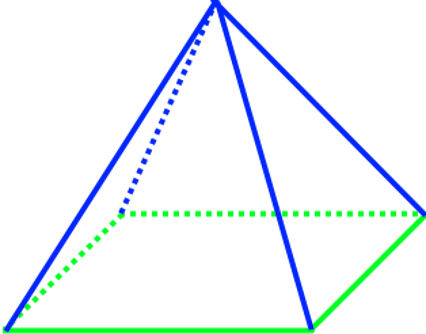
. Als ich mich dann aber hinsetzte und die Lampe von schräg unten sah, erkannte ich, dass sie
(im Gegensatz zum Galtonbrett)
dreidimensional war, nämlich eine Pyramide mit rechteckiger Grundfläche:

(vgl. eine Dunstabzugshaube:
 )
)
Nun hat aber eine Pyramide, die auf sich hält, ein quadratische Grundfläche
 ,
,
und deshalb stelle ich mir einfach vor, die Lampe hätte ebenfalls eine quadratische Grundfläche:
(Pippi Langstrumpf: "ich mach mir die Welt / widewide wie sie mir gefällt";
 )
)
Zusammen mit dem Tisch unter der Lampe ergibt sich
 .
.
In dieses Gebilde lege ich nun eine orange und eine lila Querschnitts-Fläche:


Damit erhalten wir die beiden Flächen

 .
.
Nun ist die lila Fläche allerdings perspektivisch verzerrt - und hat in Wirklichkeit dieselbe Form wie die orange Fläche:


Weil diese beiden Flächen zweidimensional sind, können
wir da Gaußkurven reinlegen (s.o.):


Um das wieder in
 einsetzen zu können,
müssen wir
einsetzen zu können,
müssen wir
 in die
perspektivische Verzerrung
in die
perspektivische Verzerrung
 (rück-)verwandeln.
(rück-)verwandeln.
 und
und
 in die
Lampendarstellung eingesetzt ergeben
in die
Lampendarstellung eingesetzt ergeben
 .
.
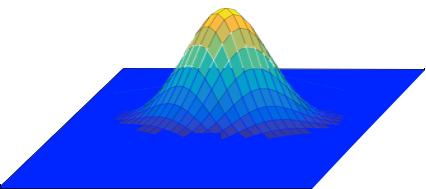
Spätestens an
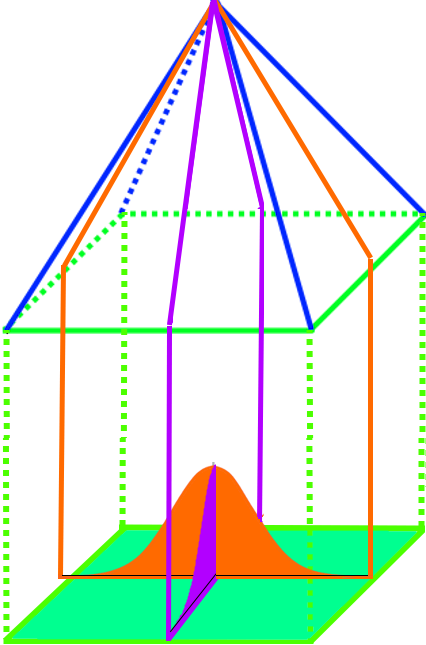 erkennt man aber
vielleicht, dass die vollständig dreidimensionale Glockenfläche so aussieht:
erkennt man aber
vielleicht, dass die vollständig dreidimensionale Glockenfläche so aussieht:
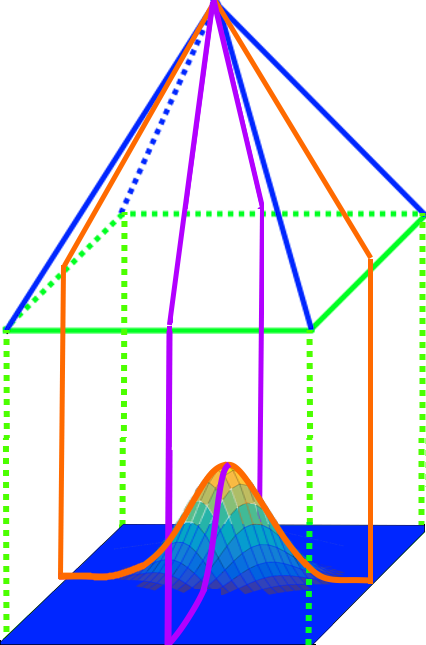
(... womit aus dem abgenagten zweidimensionalen Glockenquerschnitt eine
ganze dreidimensionale Glocke geworden ist
eine
ganze dreidimensionale Glocke geworden ist :
:
Friedrich Schiller:
Die Glocke
Fest gemauert in der Erden
Steht die Form, aus Lehm
gebrannt.
Heute muss die Glocke werden
Frisch Gesellen, seid zur Hand.
Von der Stirne heiß
Rinnen muss der Schweiß,
Soll das Werk den Meister
loben,
Doch der Segen kommt von oben.
[...]
In meinen Augen sieht das Ergebnis
 allerdings eher aus wie
ein Hügel
allerdings eher aus wie
ein Hügel
 [nur steiler] oder wie
das Dach dieses Hotels in Shenzhen [China]:
[nur steiler] oder wie
das Dach dieses Hotels in Shenzhen [China]:
 )
)
Die Erkenntnis, dass in der Lampe
 die "Gaußfläche"
die "Gaußfläche"
 steckt, ist mir allerdings beim Ansehen der Lampe
steckt, ist mir allerdings beim Ansehen der Lampe
(wie aus didaktischen Gründen oben)
auf langen Umwegen.
Aber das ändert nichts daran, dass ich überhaupt erst durch die Lampe auf die mir bis dahin unbekannte dreidimensionale "Gaußfläche" gekommen bin:

![]()

Es war also nicht so, dass die Lampe

![]()

Die Lampe war also
(für mich notwendige)
Die Lampe hat also erheblich mehr geleistet als das, was bereits oben beschrieben wurde:
| Vielleicht sind sogar die vielgeschmähten "eingekleideten" (Pseudo-)Anwendungsaufgaben viel besser als ihr Ruf, nämlich in Wirklichkeit beste Veranschaulichungsaufgaben, bei denen beispielsweise eine technische Anwendung "nur" dazu dient, Innermathematisches besser zu verstehen (und nicht umgekehrt die Mathematik dazu, eine bessere Technik zu erhalten) [...]: die ganze Welt [...] ist geeignet, wenn nicht geradezu dazu geschaffen, die Mathematik zu veranschaulichen. |
|
Es geht in diesem Essay
 der
Normalverteilung,
der
Normalverteilung,
(die für Schulen auch viel zu kompliziert wäre),
Die Lampe
 hat mich nicht nur zu
hat mich nicht nur zu  geführt, sondern zeigt auch, wie man eine dreidimensionale Version des Galtonbretts
geführt, sondern zeigt auch, wie man eine dreidimensionale Version des Galtonbretts
 bauen könnte: man nehme einen
bauen könnte: man nehme einen

Perlenvorhang,
wie er oft vor Türöffnungen
 gehängt wird
gehängt wird
(die grauen Kugeln entsprechen den Glaskugeln in der
Lampe
 ),
),
und montiere dahinter versetzt weitere Perlenvorhänge:

Und dann lasse man von oben
Kugeln durch dieses
Gitternetz rieseln. Sie werden sich mit großer Wahrscheinlichkeit unten
annähernd so
 anhäufen.
anhäufen.
Leider ist die Lampe aber nur ein "halbguter" Tipp: eine
in dem Gitter herabfallende Kugel kann nicht exakt von
oben auf eine
nächsttiefere Gitterkugel
fallen, weil da der Faden bzw. die
Stange im Weg
ist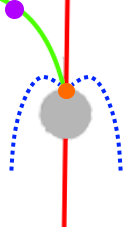 Dadurch sind die
weiteren Fallrichtungen aber nicht gleichwahrscheinlich.
Dadurch sind die
weiteren Fallrichtungen aber nicht gleichwahrscheinlich.
(Nebenbei:
 erinnert
mich doch sehr an
erinnert
mich doch sehr an


Conrad Ferdinand Meyer:
Aufsteigt der Strahl und fallend gießt
Er voll der
Marmorschale Rund,
Die, sich verschleiernd, überfließt
In einer zweiten
Schale Grund;
Die zweite gibt, sie wird zu reich,
Der dritten wallend
ihre Flut,
Und jede nimmt und gibt zugleich
Und strömt und ruht.
Da sich ein senkrechtes Gitter als ungünstig erwiesen hat, habe ich überlegt, ob ein waagerechtes Gitter besser geeignet wäre.
Man nehme also
schwarze Gitter
 und
rote Gitter
und
rote Gitter
 und
staple sie abwechselnd derart übereinander, dass die Knotenpunkte der
roten
Gitter immer (von oben gesehen) genau in der Mitte der
schwarzen Quadrate
liegen:
und
staple sie abwechselnd derart übereinander, dass die Knotenpunkte der
roten
Gitter immer (von oben gesehen) genau in der Mitte der
schwarzen Quadrate
liegen:

Wieder schräg von der Seite gesehen ergibt sich dann
 .
.
Ein erstes mit
![]() gebautes Modell sieht
dann so aus
gebautes Modell sieht
dann so aus
(... wobei alle Teile weggelassen wurden, durch die die Kugeln sowieso nicht fallen können, sich also die Pyramidenform ergibt):

Wenn man dieses Modell von der Seite ansieht
 ,
erkennt man, dass
,
erkennt man, dass
Um nun herauszufinden, wie die von oben herunterrieselnden Kugeln fallen, schauen wir uns das Modell von oben an
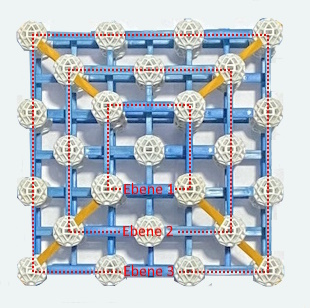
und dann nacheinander die Ebenen :

Erst fällt eine Kugel durch das Loch
 in der
Ebene 1
in der
Ebene 1
 oder
oder
 oder
oder
 oder
oder
 in der
Ebene 2
in der
Ebene 2(dabei hat jede der vier
Fallrichtungen
 ,
,
 ,
,
 und
und
 dieselbe Wahrscheinlichkeit
dieselbe Wahrscheinlichkeit
![]() , d.h.
die Wahrscheinlichkeitsverteilung ist "gleichverteilt").
, d.h.
die Wahrscheinlichkeitsverteilung ist "gleichverteilt").
Statt der zwei möglichen Fallrichtungen bei der Bi(= zwei)nomialverteilung gibt es hier also vier mögliche Fallrichtungen, so dass man auch von einer "Tetra(= vier)nomialverteilung" sprechen könnte.

 oder
oder
 oder
oder
 oder
oder
 :
:

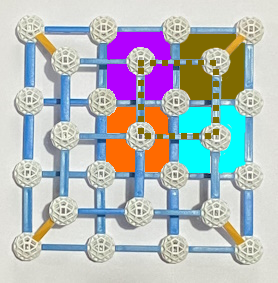
 oder
oder
 oder
oder
 oder
oder
 :
:

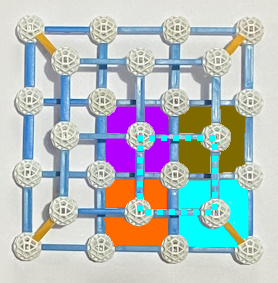
 oder
oder  oder
oder  oder
oder
 :
:

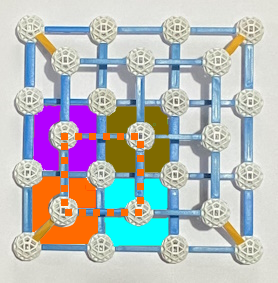
 oder
oder
 oder
oder
 oder
oder
 :
:
 :
: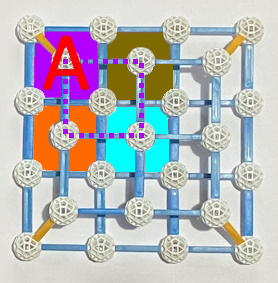 erreicht:
erreicht: ;
;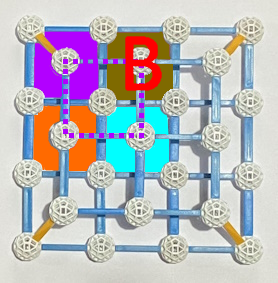 und
und
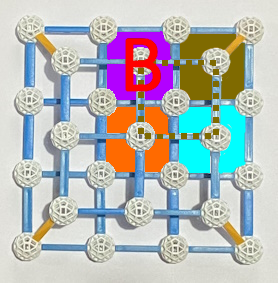 erreicht:
erreicht: ;
; erreicht:
erreicht: ;
;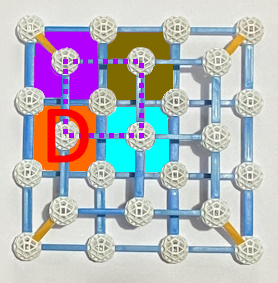 und
und
 erreicht:
erreicht: ;
;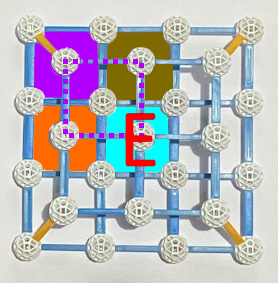 und
und
 und
und
 und
und
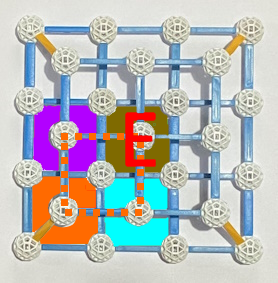 erreicht:
erreicht:  ;
;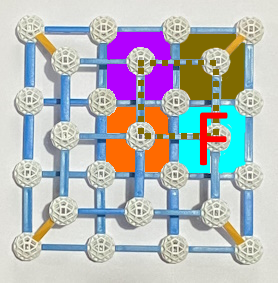 und
und
 erreicht:
erreicht: ;
; erreicht:
erreicht: ;
;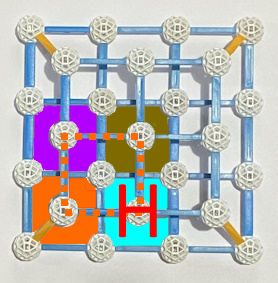 und
und
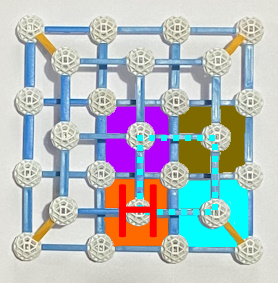 erreicht:
erreicht:
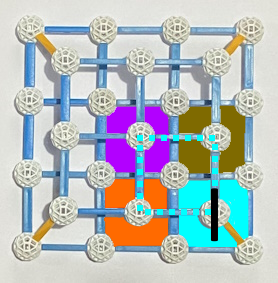 erreicht:
erreicht: .
. .
.

 und deshalb auch
und deshalb auch


 ;
; ;
; die
herabfallenden Kugeln völlig aus den Augen verloren. Deshalb schauen
wir uns an drei Beispielen mal an, wie die Kugeln durch die
Ebenen
hinunterfallen:
die
herabfallenden Kugeln völlig aus den Augen verloren. Deshalb schauen
wir uns an drei Beispielen mal an, wie die Kugeln durch die
Ebenen
hinunterfallen: ?:
?:


 bzw.
bzw.


 .
. 

 ,
,


 ,
,


 .
.
Eine Kugel kann also nur auf
![]() (eine) Art in eines der
(eine) Art in eines der ![]() -Löcher fallen,
nämlich indem sie zwei Mal in dieselbe Richtung fällt.
-Löcher fallen,
nämlich indem sie zwei Mal in dieselbe Richtung fällt.
 ?:
?:

 oder
oder

 oder
oder 
 oder
oder
 bzw.
bzw.


 oder
oder


 .
. Entsprechend
gilt für die anderen ![]() -Löcher:
-Löcher:


 oder
oder


 ,
,


 oder
oder


 ,
,


 oder
oder


 .
.
Eine Kugel kann auf
![]() Arten in eines der
Arten in eines der ![]() -Löcher
fallen, nämlich indem sie
-Löcher
fallen, nämlich indem sie
 ?:
?:

 oder
oder
 oder
oder
 oder
oder 
 oder
oder
 oder
oder
 oder
oder

 oder
oder
 oder
oder
 oder
oder



 oder
oder 

 oder
oder 

 oder
oder 

 .
.
Eine Kugel kann also auf
![]() Arten in das
(einzige)
Arten in das
(einzige)
![]() -Loch fallen, nämlich
-Loch fallen, nämlich
 16
Kugeln hinein wirft, landen sie unter der Ebene 3 mit großer Wahrscheinlichkeit
so:
16
Kugeln hinein wirft, landen sie unter der Ebene 3 mit großer Wahrscheinlichkeit
so:

 , ergibt sich im Dreidimensionalen
, ergibt sich im Dreidimensionalen
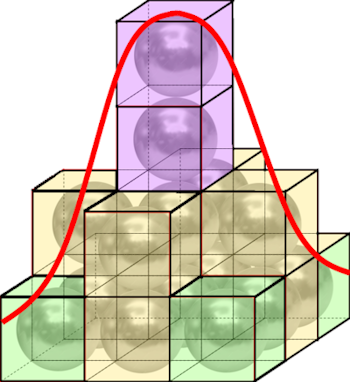 ,
d.h. es ergibt sich schon annähernd eine Gaußsche
Glockenfläche und insgesamt etwa
,
d.h. es ergibt sich schon annähernd eine Gaußsche
Glockenfläche und insgesamt etwa
 .
.| PS: | hier soll nicht der eigentlich
ja interessanteste und überhaupt erst im eigentlichen Sinne
mathematische Schritt gegangen werden, nämlich die Klärung der Frage,
(z.B. n = 1000, also Ebene 1000) hin verändert
(und sich damit die Betrachtung aller Zwischenebenen [z.B. Ebene 1, Ebene 2, Ebene 3 ... Ebene 999] sparen kann). |