Vgl. .

Es ist (wieder mal) , dass heutzutage immer weniger Leute (klassische) Bildung, sprich: das GROSSE Latinum und das Graecum haben.

Gebildete Menschen wissen selbstverständlich, dass

• zum Singular "Minimum" der Plural "Maxima" lautet

• und entsprechend zum Singular "Maximum" der Plural "Maxima" lautet.

Lustiger finde ich aber dennoch die Plurale "Minimums" und "Maximums".

Das Internet vergisst nichts, also auch nicht

• dieses Highlight

• oder "Wenn Fußballtrainer KOMPLETT ausrasten...":

.

Erstaunlicherweise fehlt in dieser Liste der Trainer-Ausraster aber Rudi Völlers legendärer Wutausbruch:

1. „[…] diese Geschichte immer mit dem [ersten] Tiefpunkt [T₁]“:

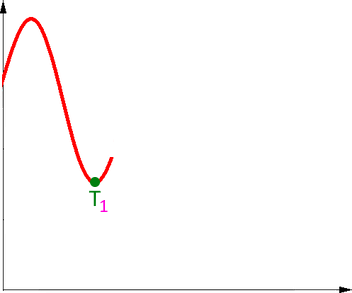
2. „und nochmal ein [zweiter] Tiefpunkt [T₂]“:

hier gibt es drei Möglichkeiten:

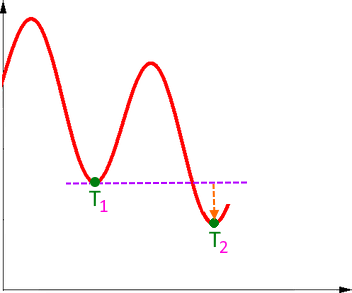
1. ein zweiter Tiefpunkt T₂ , der allerdings höher liegt als der erste Tiefpunkt T₁ :

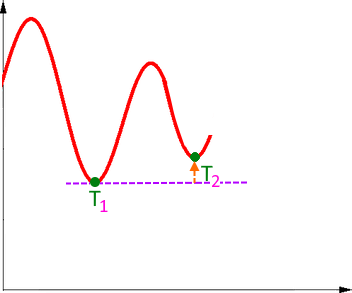
2. ein zweiter Tiefpunkt T₂ , der genauso hoch liegt wie der erste Tiefpunkt T₁ :

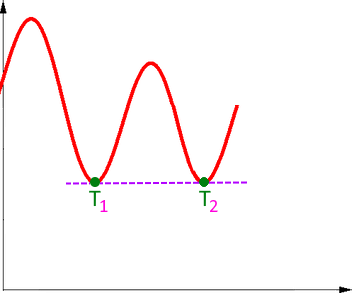
3. ein zweiter Tiefpunkt T₂ , der tiefer liegt als der erste Tiefpunkt T₁ :

3. „und dann gibt's nochmal einen niedrigeren [dritten]Tiefpunkt [T₃]“:

Daraus folgt zu allererst, dass T₃ tiefer liegt als T₂ .

Ansonsten ist allerdings nicht klar, was genau Völler gemeint hat:

1. dass mit T₃ ein dritter Tiefpunkt folgt, der allerdings zum ersten Mal niedriger als sein Vorgänger (T₂ ) liegt, woraus folgt: T₂ lag

• höher als T₁ (vgl. 2.a.)

• oder auf gleicher Höhe wie T₁ (vgl. 2.b.);

2. dass T₂ auch schon tiefer als T₁ lag (vgl. 2.c.).

Ich unterstelle mal, dass Völler b. gemeint hat, also insgesamt

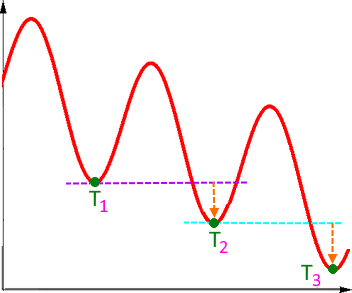
oder vereinfacht

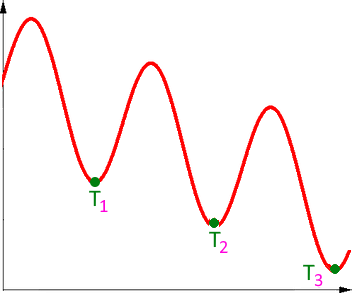
Kurz anzumerken ist natürlich:

•     ist nicht Völlers Diagnose, sondern er unterstellt sie dem Reporter Delling - und hält sie für „Scheißdreck“;

• die so hübsch geschwungene Kurve ist natürlich eine mathematische Idealisierung: reale Fußballergebnisse ergeben wohl kaum eine solch gleichmäßige Entwicklung;

• an der Kurve interessieren uns (und Völler) nur die immer weiter abfallenden Tiefpunkte; denkbar wäre es aber, dass

gleichzeitig die Hochpunkte immer weiter ansteigen:  :

die Mannschaft würde dann abwechselnd z.B.

• bei Auswärtsspielen (ohne Rückhalt durch ) immer schlechter

• und bei Heimspielen (mit ) immer besser spielen.

Bleiben wir aber bei :

• was nun eigentlich ist ein "Tiefpunkt",

• und was besagt es eigentlich, wenn Völler von " nochmal einen niedrigeren Tiefpunkt" gesprochen hat?

... wobei man wohl vermuten darf, dass Völler die allermeiste Mathematik aus seiner Schulzeit Jahrzehnte später längst gründlich vergessen hatte.

Aber anscheinend bedarf es dieser Schulmathematik gar nicht, um fundamentale Tatsachen der Mathematik zu begreifen. Ja, vielleicht zerstört die übliche Schulmathematik sogar die einfache Mathematik des "gesunden Menschenverstands"

(allerdings ist der „gesunde Menschenverstand oftmals nur eine Verallgemeinerung der eigenen Vorurteile [aus „ich“ wird „die Mehrheit“] und taucht dann oft als antiwissenschaftliches „Argument“ auf).

Vielleicht hat Völler ganz anschaulich gedacht:

• T₁ ist der tiefste Punkt im 1. Tal,

• T₂ ist der tiefste Punkt im 2 Tal,

• T₃ ist der tiefste Punkt im 3. Tal,

• aber die Täler werden von links nach rechts immer tiefer:

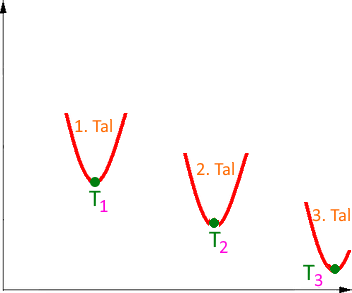
Dabei

• sind die Hochpunkte (Berggipfel) völlig uninteressant,

• und überhaupt liefern die Berge nur die Seitenwände der Täler.

Die Tiefpunkte sind ganz einfach

• die tiefsten Punkte in ihrer direkten (linken und rechten) Umgebung.,

• aber nicht unbedingt die tiefsten Punkte der ganzen Gegend.

DinTiefpunkt T₁ und T₂ nennt man „lokale“ Tiefpunkte, da sie

• nur die tiefsten Punkte in ihren Tälern sind,

• aber nicht die tiefsten Punke der ganzen Gegend.

Den Tiefpunkt T₃ und T₂ nennt man „absoluten“ Tiefpunkt, da er

• nicht nur der tiefste Punkte in seinem Tal ist,

• sondern auch der tiefste Punkt der ganzen Gegend.

Wenn man die tiefsten Punkte von Tälern sucht, suche man einfach nach halbwegs stehendem Wasser:

Wenn man aber auch unter der Wasseroberfläche weitermisst, gilt:

• der höchste Berg der Erde (das absolute Maximum) ist der Mount Everest (Höhe ca. 8,9 km über dem Meeresspiegel)

• das tiefste Tal der Erde (das absolute Minimum) ist der Marianengraben (Tiefe ca. 10,9 km unter dem Meeresspiegel)   ;

• wenn man aber von der Basis jedes Berges ausgeht,

  • ist der weitgehend unbekannte Mauna Kea auf Hawaii der höchste Berg der Erde (das absolute Maximum: ca. 10,2 km über dem Meeresgrund, davon allerdings "nur" 4,2 km über dem Meeresspiegel );

  • und so gesehen ist der Mount Everest "nur" ein lokales Maximum, weil sein Gipfel "nur" ca. 5,2 km über seiner Basis liegt

(und dennoch ist sein Gipfel am weitesten vom Erdmittelpunkt entfernt, also doch wieder ein absolutes Maximum);

Das absolute Maximum aller Berge im Sonnensystem ist aber der "Olympus Mons" auf dem Mars (ca. 22 km hoch!):