 bewegte Mathematik
bewegte MathematikNewtons  bewegte Mathematik
bewegte Mathematik

"Und sie [die Mathematik] bewegt sich doch!"
| "Im 5. und 6. Jahrhundert v. Chr. hatten sich das Sehvermögen und die Attribute der Erkenntnis in dem griechischen Wort theorein verbunden, das sowohl »anschauen« als auch »erkennen» bedeutet. "Chemiker zeichnen [...] starre Strukturen und verleihen ihren Gebilden eine widerstandsfähige dreidimensionale Ordnung. [Der Nobelpreisträger Robert] Woodward sah die Dinge anders: er betrachtete Moleküle als etwas Fließendes." |
Fast alle mathematischen und physikalischen Details, die angeblich erst Newton entdeckt hat (beispielsweise das Trägheitsgesetz), waren schon vorher bekannt (das Trägheitsgesetz z.B. dem Physiker Hook, einem älteren Zeitgenossen Newtons). Nur mindert das ja nicht im mindesten Newtons Leistung: er war der erste, der die vorherigen Kenntnisse (oder doch eher Ahnungen?) genial zusammengebracht und um wichtige Details erweitert hat.
Das einmalige Genie Newtons bestand darin, in Mechanik und Geometrie ein und dasselbe (nämlichen den Schöpfungsplan Gottes!) zu sehen.
Da wundert es (fast) gar nicht mehr, daß er die mechanische Bewegung auf die Geometrie übertragen hat.
Der Weg ist also vermutlich folgendermaßen verlaufen: Newton hat die mechanische Bewegung des freien (senkrechten!) Falls etwa eines Steins in ein geometrisches Koordinatensystem übertragen, das dann (in moderner Fachsprache und moderner grafischer Notation) etwa folgendermaßen aussah:
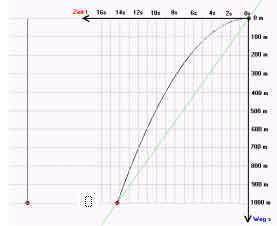
(vgl. das zugehörige Programm in
![]() )
)
Solche geniale Abstraktion (die allerdings schon auf der ebenso genialen Erfindung des Koordinatensystems durch Descartes beruhte) finde ich schlicht unglaublich. Denn man muß immerhin bedenken: der Stein fällt im freien Fall und "anschaulich" gerade runter (siehe in der Zeichnung bzw. im Programm links) und keineswegs - wie im Koordinatensystem (siehe in der Zeichnung bzw. im Programm rechts) - in einer Parabel.
Der geniale Geniestreich Newtons bestand darin, die lineare Abwärtsbewegung des freien Falls in zwei Bewegungen zu zerlegen:
eine räumliche Bewegung (im Koordinatensystem von oben nach unten),
eine zeitliche Bewegung (im Koordinatensystem von rechts nach links).
Die Genialität bestand also darin,
eben die Zeit auch als (räumliche) Bewegung zu verstehen,
alles paradoxerweise dadurch einfacher (überhaupt beschreibbar) zu machen, daß man es "schwieriger" macht, nämlich den Augenschein (linearen Fall) in die beiden Bestandteile Raum und Zeit zerlegt und sie in einer doch hübsch schwierigen Parabel darstellt.
Newton "sieht" den Stein nicht nur linear (von oben nach unten) fallen, sondern auch in einer Parabel (der Kombination von Raum und Zeit).
Vgl. nochmals das Programm "freier Fall". Nur durch solch ein Computerprogramm ist illustrierbar, was Newton da "gesehen" und innerlich erlebt haben muß.
Damit (mit der Übertragung anschaulich linearer Bewegung auf eine abstrakte mathematische Zeichnung) war aber die Voraussetzung für bewegte Mathematik gegeben, d.h. die Wahrnehmung aller Mathematik in Bewegung.
Wir sind heute nicht "besser", bzw. wir stellen uns gerade in Folge Newtons die gesamte Wirklichkeit genauso mechani[sti]sch und in Bewegung vor:
z.B. die Elektronen des elektrischen Stroms stellen wir uns als ganz kleine, sich bewegende Kügelchen vor, und das elektronische Bauteil eines "Widerstands" ist für uns nur so lange be-greiflich, wie es der Analogie eines verengten Schlauchs entspricht: vor diesem verengten Schlauch stauen sich die Kügelchen [halten notgedrungen in ihrer Bewegung inne], und da ist es kein Wunder, daß sie nur langsamer durch den Schlauch [Widerstand] hindurch können.
Aber unser Gehirn renkt sich aus, wenn diese mechanistische Kügelchen-Analogie nicht mehr klappt, wenn sie also gewisse elektronische Phänomene nicht mehr erklären kann und bei ihnen nicht mehr weiter hilft, ja, in die Irre führt. Dieses "Gehirnausrenken" ist ja gerade der fortwährende Skandal der Quantentheorie!)
Obige Grafik ist nicht mit dem Fall eines Körpers nach waagerechtem Abwurf zu verwechseln: bei einem solch waagerechten Wurfs nach links fällt der Stein ja tatsächlich parabelförmig (auf der waagerechten Achse des Koordinatensystems ist dann nach links nicht mehr die Zeit eingetragen, sondern die waagerechte Strecke).
Die Zeichnungen für den waagerechten Wurf einerseits und den senkrechten freien Fall sehen also (abgesehen von anderer Bedeutung der waagerechten Achse) absolut identisch aus und unterscheiden sich doch gewaltig:
die Zeichnung für den waagerechten Wurf entspricht weitgehend der Wirklichkeit: es ist, als hätte man ein Foto der Bewegung mit langer Belichtungszeit gemacht, so daß tatsächlich jeder eingenommene Punkt abgebildet ist
(und doch hört man hier raus, wie abstrakt auch schon solch ein Foto mit langer Belichtungszeit ist: es stellt eine Gleichzeitigkeit aller Fallpunkte erst her, die es in Wirklichkeit so nie gab, was allemal für eine Zeit enorm abstrakt war, die noch gar nicht solche Fotos machen konnte. Man bedenke immerhin, daß ganze Generationen die Parabelform des waagerechten Wurfs gar nicht gesehen haben. Sie waren fest überzeugt, ein Stein fliege erst nur waagerecht, diese waagerechte Bewegung nehme dann ab, und dann falle der Stein plötzlich senkrecht:

Ohne Trägheitsgesetz war die Parabelform auch gar nicht zu erkennen bzw. akzeptabel);
die Zeichnung für den freien (senkrechten) Fall ist hingegen pure Abstraktion: sie macht die Zeit überhaupt erst zum Raum.
Mag dennoch sein, daß Newton erst durch die Beobachtung des (parabelförmigen) waagerechten Wurfs auch auf die (parabelförmige) Abstraktion für den senkrechten freien Fall gekommen ist.
Bezeichnenderweise funktioniert´s aber letztlich umgekehrt:
erst mußte der freie senkrechte Fall verstanden werden;
dann mußte der waagerechte Wurf in zwei Bewegungen (eine lineare nach links und den freien Fall nach unten) aufgeteilt werden;
und erst dann ist die Parabelform des waagerechten Wurfs verständlich.
Und genau durch die Vorstellung der Bewegung in mathematisch-geometrischen Kurven ist Newton überhaupt erst auf seinen zweiten (und letztlich zentralen) Geniestreich, die sogenannte "Infinitesimalrechnung", gekommen.
"[Newton] orientierte sich [...] an der Methode Cavalieris (1598- 1647) [...] Für Cavalieri bestand eine Linie aus einer unendlichen Anzahl von Punkten, eine Fläche aus einer unendlichen Anzahl von Linien und ein Körper aus einer unendlichen Anzahl von Flächen. (Diese Idee hatte Pascal etwas anders formuliert: Er nahm an, eine Linie bestehe aus einer unendlichen Anzahl unendlich kleiner Linien, eine Fläche aus einer unendlichen Anzahl unendlich schmaler Quadrate, ein Körper aus einer unendlichen Anzahl unendlich schmaler Körper.) [...] 1666 erfaßte Newtons Intuition den »Punkt« als eine unendlich kurze Linie. Wie nun aber läßt sich ein so verstandener Punkt auf die Wirklichkeit, auf eine gekrümmte Linie, beziehen? [...] Und dieser Punkt ist in Bewegung, und zwar so, daß jene gekrümmte Linie entstehen kann. Ebenso verhält es sich mit Linien und Flächen. Punkte ergänzen Linien, durch die Bewegung der Linien gibt es Flächen, durch die Bewegung der Flächen Körper. [...] Ein Punkt [...] fließt gleichmäßig [...]"
(nach: Johannes Wickert: Isaac Newton)
Das Fließen bzw. der Fluß ist der Inbegriff kontinuierlicher, also nicht abgehackter, springender (Mathematiker würden sagen "stetiger") Bewegung.
Am Zitat von Wickert gibt es allerlei zu erklären:
1. zu dem was Cavalieri (und Pascal) gesagt hat:
eine Strecke (auf dem Zahlenstrahl z.B. von 1 bis 5) kann man auch als Menge sämtlicher (unendlich vieler!) Punkte auf ihr auffassen:
Da gehören dann z.B. die Punkte P1 = 2, P2 = 1,5, aber auch solch "irrationale" Punkte wie z.B. P3 = √2 ≈ 1.41421356237310 dazu.
Oder um es in Bewegung auszudrücken:
eine Strecke IST im Grunde EIN Punkt, der sich kontinuierlich bewegt.
Wieder: es ist wie ein Foto mit langer Belichtungszeit.
(Man könnte auch - geradezu quantenmechanisch gedacht - sagen: der Punkt ist potentiell überall gleichzeitig auf der Strecke und an einem bestimmten Ort nur mit einer gewissen Wahrscheinlichkeit anzutreffen.)
So gesehen IST ein Kreis ein um einen Mittelpunkt rotierender Punkt
und im Dreidimensionalen eine Kugel ein um einen Mittelpunkt wirbelnder Punkt:
"Weiterhin kann man jede Kurve auch als Bahn eines bewegten Punktes auffassen. Daß man die Bewegung eines Punktes erfassen konnte, war wichtig, denn die Bewegung an sich war ein zentraler Begriff der Philosophie jener Zeit [im 17. und 18. Jahrhundert]. Nicht nur Hobbes [1588-1679], sondern auch andere Philosophen hielten die Bewegung für die Grundlage jeder Erscheinung, gleichgültig, ob auf physikalischen oder mentalem Gebiet."
(Hal Hellman)Selbstverständlich war diese frühzeitliche Philosophie arg mechanistisch - und doch eben auch ungeheuer anschaulich.
Vor allem ist Bewegung hier aber immer stetig bzw. analog gedacht: zwischen einem Punkt A und einem Punkt B werde sukzessive alle anderen Punkte angenommen, es gibt nicht jene "digitalen" Sprünge, die erst viel später in der Quantentheorie auftauchen.
Entsprechend gilt:
eine (gleichmäßige) Fläche IST im Grunde EINE Strecke, die sich kontinuierlich bewegt.
Wieder: es ist wie ein Foto mit langer Belichtungszeit.
Und nochmals weiter gedacht:
ein (gleichmäßiger) Körper IST im Grunde EINE Fläche, die sich kontinuierlich bewegt.
Wieder: es ist wie ein Foto mit langer Belichtungszeit.
Und jetzt kann man natürlich weiterdenken: wenn
eine Strecke ein Punkt und
eine Fläche eine Strecke und
ein Körper eine Fläche in Bewegung ist,
dann ist letztlich auch ein Körper ein wild umherfliegender Punkt: "im Anfang war der Punkt"
[etwa so, wie
die Potenz eine Abkürzung der Multiplikation und
die Multiplikation wiederum eine Abkürzung der Addition,
insgesamt also die Potenz eine sehr kurze Addition ist: "im Anfang war die Addition", und aus der 1 wurden per Addition alle anderen Zahlen gezeugt].
Z.B. entsteht ja auch ein Fernsehbild [eine Fläche] durch einen Punkt, der rasend schnell nacheinander Zeilen abläuft:
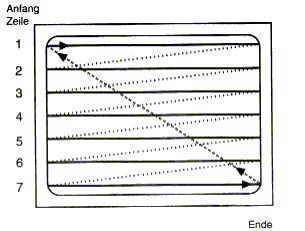
Und beim holographischen Speicher wird ein (Laser-)Punkt sogar dreidimensional gespeichert, erzeugt er (mit einem Referenzstrahl) also einen Körper.
Es geht alles vom Punkt aus, Hauptsache, er bewegt sich!
"[...] ein Punkt, der nicht durch seine Ausdehnung, sondern durch seine Wandelbarkeit [Bewegung] bestimmt wird."
(Albert Béguin)Dieses Zitat, von Béguin ursprünglich auf den Menschen im Denken Blaise Pascals bezogen, dreht die Logik geradezu um: ein Punkt wird erst definiert durch die Strecke/Fläche bzw. den Raum, die bzw. den er durchläuft.
Daß eine Linie (in Bewegung) identisch mit einer Fläche sein kann, hat der italienische Mathematiker Peano (1858 - 1932) mit den nach ihm benannten Peano-Kurven gezeigt. Ein ähnliches Beispiel ist die Hilbert-Kurve:

Dabei wird ein bestimmtes simples Konstruktionsprinzip immer erneut und ad infinitum angewandt: das Muster verfeinert sich immer mehr, und das Erstaunliche ist (Peano hat es bewiesen!), daß solch eine unendliche Linie irgendwann tatsächlich durch sämtliche Punkte einer Fläche geht, daß also die (unendliche) Linie identisch mit der Fläche ist.
Späte Folge davon war, daß in der Fraktalmathematik (fraktal = gebrochen) die klare Trennung zwischen Linien (also eigentlich Eindimensionalem) und Flächen (also Zweidimensionalem) aufgegeben und gebrochene Zwischendimensionen (z.B. 1,4) eingeführt werden mußten.
Nebenbei: mit seiner Erklärung von Flächen durch Strecken (bzw. kleinere und rechteckige Flächen) hat Cavalieri wunderbar die Scherung
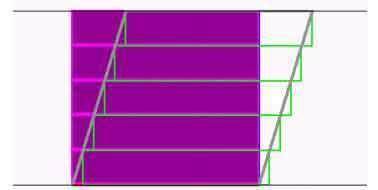
(vgl. das zugehörige Programm in
![]() )
)
anschaulich gemacht (und zwar in Bewegung, also etwa so, wie man einen Bierdeckelstapel schief schiebt).
Man kann natürlich auch umgekehrt (und das werden wir gleich brauchen)
eine Fläche als einen zusammengequetschten Körper,
eine Strecke als eine zusammengequetschte Fläche und
einen Punkt als zusammengequetschte Linie
(oder z.B. auch direkt als geschrumpften Kreis bzw. geschrumpfte Kugel)
auffassen, und dann wäre umgekehrt der Körper "die Mutter aller Dinge".
Dieses "Zusammenquetschen" passiert mit Einstein sogar ganz real, wenn man Dinge immer mehr und fast bis an Lichtgeschwindigkeit beschleunigt. Oder genauer: etwa eine Kugel sieht aus ihrer eigenen Sicht weiterhin aus wie eine Kugel, aus der eines unbewegten Beobachters aber zunehmend wie ein zusammengedrückter Ellipsoid:

Es ist fast, als würde die Kugel durch den zunehmenden Fahrtwind ("Lichtwiderstand") immer mehr zusammengequetscht.
Zudem ist nach Einstein der Endzustand, also Lichtgeschwindigkeit und damit völlige Abplattung der Kugel zu einem Kreis, unmöglich.
Insgesamt könnte man also auch sagen:
ein beschleunigter Kreis (Fläche) ist ein Zylinder (Körper),
ein noch mehr beschleunigter Zylinder wird hingegen wieder zu einem Kreis.
gilt es anschaulich zu machen, wie Newton sich die "Ableitung" und die "Integration" vorgestellt hat:
a) die Ableitung:
offensichtlich hat er genau umgekehrt zu allem eben genannten gedacht: nicht die Strecke besteht aus vielen Punkten, sondern ein Punkt ist eine unendlich kurze Strecke. D.h. er hat den so abstrakt definierten Punkt (laut Euklid ist er unteilbar) anschaulich gemacht, indem er ihn als Ministrecke aufgefaßt hat.
Auf einer gekrümmten Kurve bewegt sich bzw. fließt also eine Ministrecke von links nach rechts:
Man kann sich das so vorstellen wie eine Holzplanke, die sich permanent den wogenden Wellen des Meeres anpasst,
Hier wird schon zweierlei deutlich:
mit der Auffassung des Punktes als Ministrecke ist schon das Tangentenproblem, um das es bei der Ableitung geht, anschaulich deutlich;
die Ministrecke ist eine erstaunlich gute (und - wie gleich bei der Bergwanderung klar werden wird - gefährlich irreführende) Annäherung an die krumme Kurve, nämlich fast identisch mit ihr.
Als (Mathematik-)Lehrer sollte man sich ja sowieso zu keiner Anekdote, zu keinem Bild und keiner Erlebnisgeschichte zu schade sein
(und muß doch drauf achten, daß die Anekdoten nicht zu einseitig rüberkommen, d.h., daß SchülerInnen sich nicht einen falschen Teil merken; und zudem sollte man auch immer die Grenzen jedes Bilds beachten, also diejenigen Details, die eher in die Irre führen).
Ich erkläre den SchülerInnen einen Funktionsgraphen gerne als eine Bergwanderung (und zwar immer von links nach rechts; vgl. 3.). Und Newtons Ministrecken kann man dann mit einer Bergwanderung im Nebel
vergleichen: egal, ob man zurück oder vor schaut, man meint an jedem Punkt, in einer schrägen Ebene (Verlängerung der gegenwärtigen Ministrecke ) mit ewig gleicher Steigung zu sein:
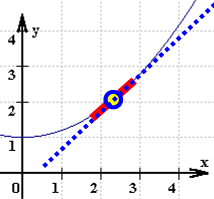
Man ahnt noch gar nicht (sieht es nicht), daß der Berg zunehmend steiler wird. Das ja eben ist die Gefahr bei Bergwanderungen im Nebel: daß alles im Tal so harmlos anfängt, an den Hängen so kaum spürbar ansteigt - und man in größter Gefahr ist, bevor man sich versieht (und dann nicht mal mehr rückwärts kann).
b) das Integral:
Newton faßt die Fläche unter der Kurve als eine sich von links (1) nach rechts (5) bewegende Strecke auf:
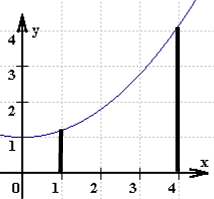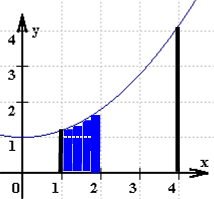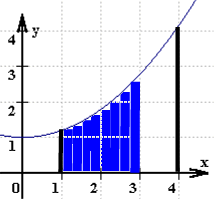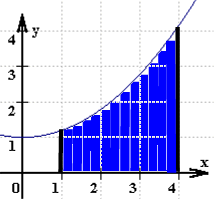
Auch mit dieser Vorstellung hat Newton wieder den entscheidenden Schritt getan: gerade das Handicap, daß man solch eine Strecke nicht beliebig dünn zeichnen kann, sondern daß sie immer rechteckförmig aussieht, führt dann zur Lösung des Problems, eine krumme Fläche zu berechnen, mittels Annäherung durch (immer schmalere) Rechtecke:
ist aber - vor aller "Hochmathematik" der Ableitung und Integration und damit schon für UnterstufenschülerInnen - Newtons "bewegte" Vorstellung einer Funktionsgraphen bemerkenswert, d.h., was Wickert nach obigen Zitat noch anfügt:
"Auch Kurven sind [für Newton] fließende Vorgänge, jedoch fließt da etwas ungleichmäßig. [...] Fließende Größen bezeichnet Newton mit dem Begriff Fluenten [lat. fluens = fließend], den mathematischen Formalismus nennt er Fluxionsrechnung. [...] y und x sind Fluenten, kurvenziehende Bewegungen. [...]"
Newton versteht also die sogenannte Abszisse und die sogenannte Ordinate als bewegt:
Die Abszisse wächst gleichmäßig von links nach rechts (und nie umgekehrt, aber auch nie mal in die eine, mal in die andere Richtung!), und in Abhängigkeit von ihr verändert sich auch die Ordinate, nur letztere eben ungleichmäßig (mal wachsend, mal fallend, mal gleichbleibend). Aus
der Bewegung der Abszisse und
der Bewegung der Ordinate
ergibt sich dann (weil jeder Punkt durch seine Abszisse und seine Ordinate definiert ist) eine Bewegung des Punkts dem Funktionsgraphen entlang (wieder von links nach rechts, aber mal nach oben, mal nach unten):
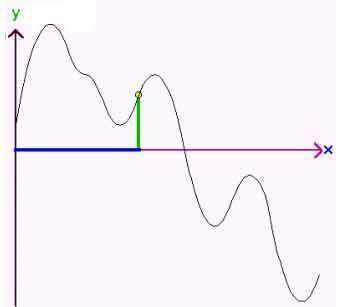
(vgl. das zugehörige Programm in
![]() )
)
Nicht nur jeder Funktionsgraph einer Einzelfunktion ist derart ein sich bewegender Punkt,
sondern auch die Graphen einer Funktionsschar (aus unendlich vielen Funktionen) sind ein sich bewegender Funktionsgraph
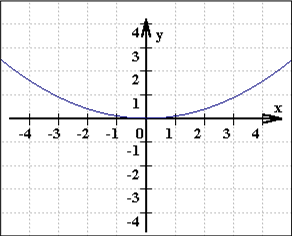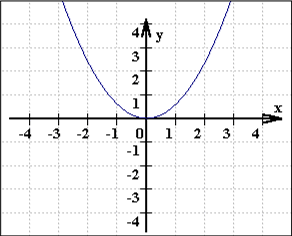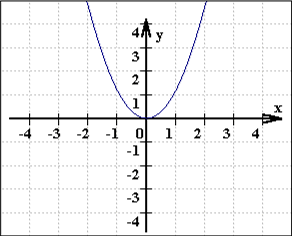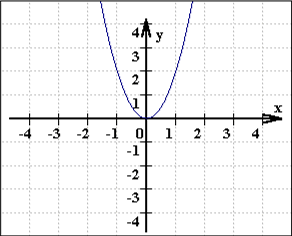

(nebenbei: ein Computer erzeugt solche Bilder ja tatsächlich, indem er irrwitzig schnell
erst nacheinander die Einzelpunkte jedes Graphen berechnet [und mit dem Kathodenstrahl auf dem Bildschirm zeichnet]
und dann jeden Einzelgraphen nacheinander.
D.h. aber doch, dass auch obiges Bild letztlich ein einziger Punkt in Bewegung ist.)
Dabei wird der Graph "gestreckt" = an den Ohren hochgezogen bzw. umgekehrt "gestaucht" = in einer Presse plattgequetscht.
Und letztlich ist eine Funktionenschar eine Fläche:
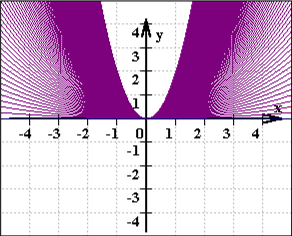
Eine Anwendung finden sich bewegende Funktionen auch bei "mehrfachen" Nullstellen: was diese sind (bzw. was solch ein rein rechnerisches Ergebnis anschaulich bedeutet und welche rechnerischen Kriterien dafür erfüllt sein müssen), wird erst deutlich, wenn man einen Graphen sukzessive so vertikal verschiebt, dass getrennt liegende Nullstellen zusammenrutschen:
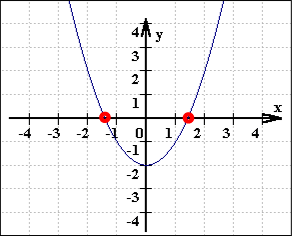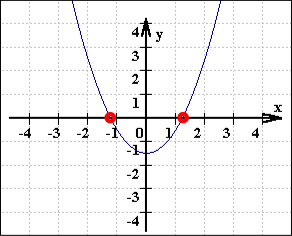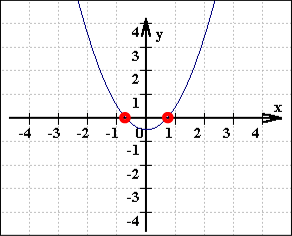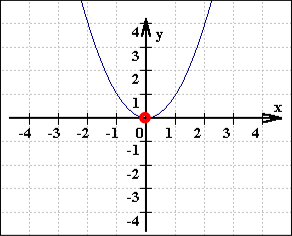
Wir alle brauchen dringend (und zwar jenseits aller "Anwendbarkeit") solche Anschaulichkeit, ja geradezu Fassbarkeit, und einE guteR MathematikerIn hat sie auch.
Umgekehrt entstehen die allermeisten Probleme von SchülerInnen dadurch, dass sie Mathematik nicht "sehen" und [wie etwa bei beim Rhythmus von a2 + b2 = c2 oder (a + b)2 = a2 + 2ab + b2] nicht "hören", dass also Mathematik für sie nicht bildende Kunst bzw. Musik wird.
(Dasselbe Problem besteht im Fach Deutsch, wenn SchülerInnen nicht bemerken, dass Literatur [und vor allem wohl Lyrik] zu einem gerüttet Maß bildende Kunst bzw. Musik ist. Bei bildender Kunst und Musik fragt man schließlich auch nicht andauernd: "was »bedeutet« das?")
Es ist keineswegs nur Vorrecht, aber auch Begrenzung der Mittelmäßigen "wie du und ich", so anschaulich-handgreiflich in Bewegung zu denken:
„»Wie wäre es, wenn man hinter einem Lichtstrahl herliefe? Wie, wenn man auf ihm ritte?« Diese hypothetischen Überlegungen hat [Einstein!] nach eigenen Angaben schon als Schüler angestellt.“
(Jürgen Neffe, Spiegel 50/1999)
Sowieso brauchen Kinder [FünftklässlerInnen] solche Anschaulichkeit, wenn Piaget erst ab ca. elf Jahren Fähigkeiten zu formal-abstrakt-hypothetischem Denken erkennt, es meiner Meinung nach aber noch bis zum Abitur geübt werden muss (weil ein 171/2jähriger letztlich auch noch [allerdings nicht nur] ein Kind ist).
| PS: | Ich bin zwar allemal auch gegen eine einseitige Kuschel- und Klötzchenpädagogik ("heart over mind", also die Kastration des Kopfes), und doch lohnt sich immerhin und allemal die Ergänzung der rein kognitiven Pädagogik durch
|
| Helmut Köckenberger: | |
| Bewegtes Lernen | |
| Lesen, schreiben, rechnen lernen mit dem ganzen Körper | |
| Verlag modernes Lernen | |
| PPS: |