 zweiter Teil
zweiter Teiloder
warum es NICHT ums RECHNEN geht
2023: der PISA-Katastrophe
 zweiter Teil
zweiter Teil
oder
warum es NICHT ums RECHNEN geht

Schadenfreude ist die schönste Freude:
![]()

Und es gab auch inhaltliche Probleme:
 ist (jetzt im Jahr 2023) wieder mal voll am Arsch:
ist (jetzt im Jahr 2023) wieder mal voll am Arsch:
Weitere nationale Demütigungen:

*
Chuck Norris ...
| ... ist ab heute Vorstandsvorsitzender
der Deutschen Bahn. Ab morgen fahren alle Züge pünktlich. |
... ist
ab heute
in Personalunion Trainer der Damen- und Herren-Fußball-Nationalmannschaft. Morgen sind wir (!) wieder Doppel-Weltmeister. |
... setzt ab morgen die (Schul-)Bürokratie auf Diät, schafft die "kalte Progression" ab, führt eine strenge Lobbykontrolle ein und verkleinert den Bundestag. |
Last but not least:
und als sich Deutschland bei den PISA-Tests im Laufe der Jahre langsam berappelt hatte, folgte
 zweiter
Teil:
zweiter
Teil:Das Land der Dichter und Denker
 ist
doch arg auf den Hund gekommen.
ist
doch arg auf den Hund gekommen.
Könnte es sein, dass Deutschland u.a. deshalb immer so grottenschlecht bei PISA abschneidet, weil die deutschen Schüler
(im Gegensatz zu denen der in PISA-Tests besseren Nationen)
die PISA-Tests
(deren Ergebnisse ja nicht in die Schulnoten eingehen)
ohne jeden Ehrgeiz runterreißen und ihre Kreuze sogar teilweise aus Jux und Dollerei zufällig setzen?
Dann wären die deutschen Schüler immerhin schlauer als "die" deutsche Öffentlichkeit, die nach jedem vergeigten PISA-Test verlässlich in Krokodilstränen ausbricht.
In PISA-Tests werden immer drei Bereiche abgeprüft:
natürlich die Mathematik!!!,
Naturwissenschaften,
was eigentlich selbstverständlich sein sollte: Lesefähigkeit.
(am besten als Lese- und Verständnisfähigkeiten bei Aufgaben, in denen die Mathematik auf alles Wichtige im Leben, d.h. auf Naturwissenschaften und Technik / Informatik
[die Heilige Vierfaltigkeit
 ]
]
angewandt wird;
ich vermute nämlich, dass viele deutsche Schüler die diesjährigen PISA-Matheaufgaben gar nicht verstanden haben und deshalb auch nicht weiterrechnen [?] konnten; s.u.).
Mit der Beschränkung auf die drei Bereiche ist schon klar, dass bei PISA ein höchst einseitiger Bildungsbegriff angewandt wird.
Jeder PISA-Test hat einen besonderen Schwerpunkt, und diesmal war es zum dritten Mal die Königin aller Wissenschaften, also die Mathematik:
"Mathematik ist ein Kernfach, es gilt als Indikator für die schulische Leistungsfähigkeit insgesamt."
"[...] Mathe, das zentralste aller Kernfächer [...]"
(Quelle:
![]() )
)
So gesehen gibt es folgende Arten von Schulfächern:
Nebenfächer
(die, wie der Name schon sagt, nebensächlich sind und die man also problemlos abschaffen könnte; also z.B. Sport, Kunst, Musik und Geschichte und sowieso Philosophie; man könnte auch sagen: der Schrott oder der Pöbel unter den Schulfächern),
Hauptfächer
(wie z.B. Englisch, Französisch, Deutsch und Mathematik),
und da
(wie z.B. Englisch [!?] und Französisch),
(die von Schülern in der Oberstufe grundsätzlich nicht abgewählt werden können, nämlich die beiden von mir unterrichteten Fächer Deutsch und Mathematik; mein Gott, bin ich wichtig!),

"das zentralste aller Kernfächer", also die Königin aller Wissenschaften: Mathematik:

oder

oder
"Mathematik ist das Alphabet, mit dessen Hilfe
Gott das Universum beschrieben hat."
(Galileo Galilei)
oder
"Die
Geometrie [und Mathematik] gab es schon vor der Erschaffung der Welt. Sie ist
ewig wie der Geist Gottes."
(Johannes Kepler)
Das ist doch schlichtweg arrogant, anmaßend, machohaft - und angesichts der Fülle der Welt herzhaft naiv!
Also bittschön ein bisschen mehr Demut!:
"Auch wenn ich es für unwahrscheinlich
halte, ziehe ich die Möglichkeit in Betracht, dass
außerirdische Besucher, denen wir irgendwann in der
Zukunft stolz unsere Gleichungen zeigen, nur höflich
lächeln und uns sagen, sie hätten ebenfalls mit der
Mathematik angefangen, dann aber die wahre Sprache
der Realität entdeckt."
(Brian Greene)
Der "Spiegel" titelte nach der Katastrophe prompt:

: das oberlehrerhafte
![]() hätte ich
natürlich weggelassen: es ist unnötig, den Leser mit der Nase auf den Fehler
zu stoßen.
hätte ich
natürlich weggelassen: es ist unnötig, den Leser mit der Nase auf den Fehler
zu stoßen.
zum Gesamtsatz
![]() :
:
(vgl.
):
mit dem "Warum" wird eine Frage angedeutet
(also "Warum müssen wir wieder rechnen lernen?"; nicht zu verwechseln mit der offenen und damit demokratischen Frage "Müssen wir wieder rechnen lernen?"),
die dann aber hinterhältig in eine Antwort umgebogen wird: "Wir verklickern euch jetzt mal, warum wir wieder rechnen lernen müssen."
müssen wir
![]() lernen, was wir
schon mal konnten, bzw. wir müssen uns wieder auf die urdeutsche
Tugend des Rechnens rückbesinnen:
lernen, was wir
schon mal konnten, bzw. wir müssen uns wieder auf die urdeutsche
Tugend des Rechnens rückbesinnen:
 .
.
zum
![]() :
:
da haben nicht etwa nur "die" deutschen Schüler
versagt, sondern
![]() alle inkl. der erwachsenen Redakteure des
"Spiegel" und dessen Leser. Bzw. das Versagen der Schüler wird (wegen
einer deutschen Kollektivschuld?) mit der nationalen
Kollektivstrafe
alle inkl. der erwachsenen Redakteure des
"Spiegel" und dessen Leser. Bzw. das Versagen der Schüler wird (wegen
einer deutschen Kollektivschuld?) mit der nationalen
Kollektivstrafe ![]() geahndet.
geahndet.
Müssen aber wir alle wieder rechnen lernen, um als Eltern unseren dummen Kindern Nachhilfe im Rechnen zu geben, also das nachzuholen, was die Schule versäumt hat?
Man stelle sich mal vor, dass
![]() (= alle
Deutschen) ab sofort abends in der Volkshochschule Rechnen büffeln, um
Deutschland nach der PISA-Katastrophe
(= alle
Deutschen) ab sofort abends in der Volkshochschule Rechnen büffeln, um
Deutschland nach der PISA-Katastrophe
 wieder aufzubauen
wieder aufzubauen
 , und am Ende stellt
sich dann heraus, dass gar nicht das Rechnen das Problem war.
, und am Ende stellt
sich dann heraus, dass gar nicht das Rechnen das Problem war.
Und was haben die Leute bloß?: immerhin sind
![]() doch
doch
 trennungsweltmeister
und damit die Speerspitze der Moral!
trennungsweltmeister
und damit die Speerspitze der Moral!
aus dem, was bei PISA noch "Mathematik" hieß, ist
im "Spiegel" simples ![]() geworden
geworden
Dass Mathematik mit Rechnen gleichgesetzt wird, unterläuft dem "Spiegel" nicht nur ein Mal:
Vielleicht ist der "Spiegel" aber gar nicht so blöd, die Mathematik mit schnödem Rechnen zu verwechseln
(Mathematik = Rechnen),
sondern meint er dem PISA-Test entnehmen zu können, dass die zentrale Fehlerquelle deutscher Schüler
wenn die deutschen Schüler besser rechnen könnten, würden sie in PISA-Tests erheblich besser abschneiden.
Ich konnte bislang keine detaillierten Untersuchungen dazu finden,
Zu 1., also der Frage, warum etwa die Hälfte aller an PISA teilnehmenden Staaten besser abgeschnitten hat:
Deutschland liegt etwa in der Mitte der teilnehmenden Staaten und immer noch knapp über dem OECD-Durchschnitt.
(Letzteres liegt allerdings nur daran, dass die "untersten" Staaten [Griechenland bis Kolumbien] so heillos versagt haben;
bemerkenswert ist aber doch auch, dass ein Großteil der Staaten [inkl. Deutschland] etwa gleichauf bei 460 bis 490 Punkten liegt [die Abweichungen da also bei lächerlichen 3 % liegen] und es nur oben und unten ganz wenige Ausreißer [Streber bzw. Versager] gibt; warum also die ganze Aufregung?):
(Nebenbei:
 auf seinen
Lorbeeren ausgeruht;
auf seinen
Lorbeeren ausgeruht;[weiß aber nicht mehr, wo]
dass Deutschland im neuesten PISA-Test ohne Berücksichtigung der
[was immer man darunter versteht:]
"Migranten" um sechs Plätze besser oder sogar auf Platz sechs stünde. Wenn das stimmen würde, hieße das aber doch,
[außer im Hinblick auf die schulische Bildung von "Migranten"-Kindern]
kein besonders großes Schulproblem.
Was aus dem schulischen "Migranten"-Problem folgen müsste:
Man nennt das wohl "Gesamtschule".)
Dass Deutschland aber noch mit einem blauen Auge davongekommen ist, reicht dem ebenso gebeutelten wie ehrgeizigen deutschen Selbstbewusstseins natürlich nicht.
Bislang sind mir nur aus dem bereits oben genannten
"Spiegel"-Artikel
![]()
einige wenige, arg
subjektive Darstellungen von Austauschschülern dazu bekannt, weshalb andere
Staaten besser bei PISA abgeschnitten haben:
Eine halbwegs einheitliche Linie (ein Patentrezept)
erkenne ich da aber nicht.
Zu 2., also der Frage, woran genau so viele deutsche Schüler im PISA-Mathe-Test gescheitert sind:
wie bereits oben gesagt, habe ich bislang auch dazu nichts Genaueres finden können.
Aber immerhin hat der "Spiegel" in dem Artikel
![]()
 die (alle?)
neuen PISA-Mathematikaufgaben veröffentlicht, und vielleicht lassen sich anhand
dieser ja doch Vermutungen anstellen, weshalb "die" deutschen Schüler so
schändlich versagt habe
die (alle?)
neuen PISA-Mathematikaufgaben veröffentlicht, und vielleicht lassen sich anhand
dieser ja doch Vermutungen anstellen, weshalb "die" deutschen Schüler so
schändlich versagt habe
(wegen mangelnder Rechenfähigkeiten?).
(ohne die vom "Spiegel" mitgelieferten richtigen Ergebnisse):







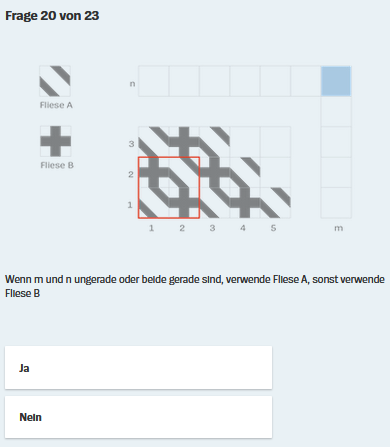


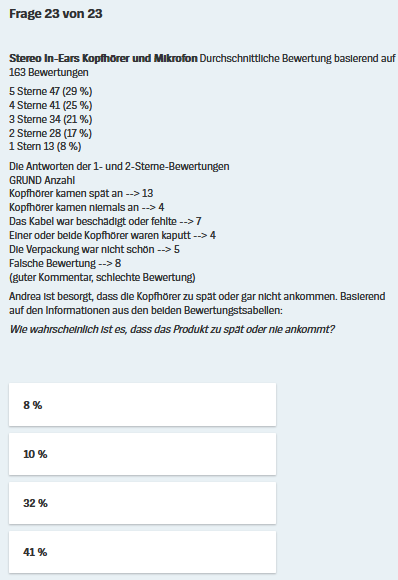
(Nebenbei ein [zugegeben: nicht sonderlich wichtiger] Einwand: weil die Aufgabenstellungen nicht immer Fragen, sondern manchmal Behauptungen sind, ist es ungünstig, die Aufgaben in den Überschriften als "Fragen" zu bezeichnen.)
Dazu einige Anmerkungen:
(weshalb ich im Folgenden keine endgültigen Aussagen darüber machen kann, was im Gesamt-PISA-Test vorkam - und was nicht [z.B. Rechnen].
Aber ich hoffe mal, dass die Beispiele vom "Spiegel" halbwegs repräsentativ ausgewählt wurden.
Und doch: wer, zum Teufel, kommt denn auf die durchgeknallte Idee, Schüler in einem Test durch sogar mehr als 23 Aufgaben zu hetzen? Ob ein Schüler was kann, ist doch auch mit zehn [kurzen] Aufgaben herauszufinden. Vgl. mündliche Abiturprüfungen, bei denen oft schon nach fünf Minuten klar ist, ob ein Schüler was kann - oder nicht.)

 , sah im Original-PISA-Test hübscher aus und hatte auch ein
übersichtlicheres Layout:
, sah im Original-PISA-Test hübscher aus und hatte auch ein
übersichtlicheres Layout:
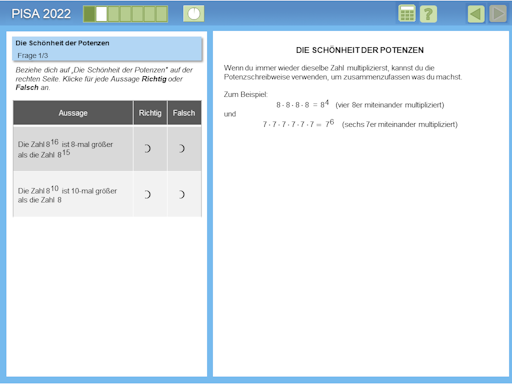 .
. ("Die Schönheit der Potenzen"
 hört sich aber
doch arg pompös an. Ich bezweifle, dass die Schüler das [zudem in der
Prüfungssituation] nachvollziehen konnten.)
hört sich aber
doch arg pompös an. Ich bezweifle, dass die Schüler das [zudem in der
Prüfungssituation] nachvollziehen konnten.)
Die 23 Aufgaben ("Fragen") lassen sich in fünf Gruppen aufteilen:
 ,
, ,
,
 .
.
 |
Es sind natürlich nicht ranzige (stilvolle!) Steinzeitkopfhörer
 , sondern
"In-Ears Kopfhörer" , sondern
"In-Ears Kopfhörer"(besser mit keinem
Bindestrich oder zwei Bindestrichen)
aus der unfassbar authentischen Lebenswelt der Schüler (obwohl nur alte Säcke den Plural "In-Ears",
junge Leute hingegen immer den Singular "In-Ear" benutzen).
Aber Schüler sind wohl kaum so blöd, sich durch solch aktualitätsgeile Anbiederung ködern zu lassen (und
bei der Mathematik der Aufgaben hilft der "In-Ears Kopfhörer"
auch nicht).
Fragt sich nur, wie in die Aufgaben der eher aus der Generation der Prüfer als der Geprüften stammende Name "Andrea" reingerutscht ist:
(obwohl
der Kauf von [zudem top-modernen] Kopfhörern ja nicht gerade peinlich
ist)?
|
|
 |
Der "Spiegel" liefert bei jeder Frage auch mit, ob eine Antwort richtig oder falsch ist. Aber es wird kaum jemals verständlich erklärt, warum eine Antwort richtig oder falsch ist.
(Beispielsweise erhält man bei Frage 16 nur die Antworten
 oder
oder
 . Bei letzterem wird
also nur gezeigt, was richtig ist, aber nicht, warum das so
ist.)
. Bei letzterem wird
also nur gezeigt, was richtig ist, aber nicht, warum das so
ist.)
Deshalb versuche ich im Folgenden immer verständliche Erklärungen
(teilweise angereichert mit Aufgabenkritik und pädagogischen Überlegungen).
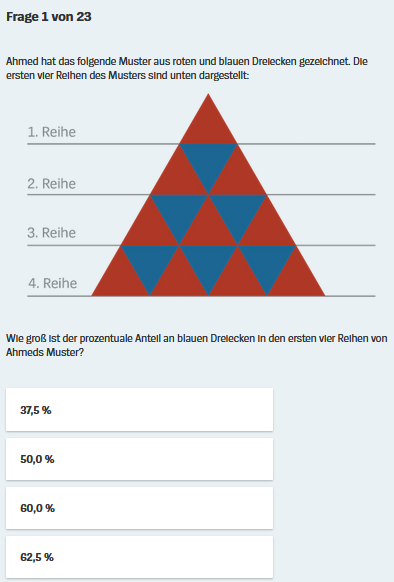
Zu Frage 1 - 3:  :
:

(Nebenbei: bunte Dreiecke werden nicht [nur] "gezeichnet", sondern [auch] [aus-]gemalt.
Ich halte es zudem für hilfreich, dass Ahmed die
Dreiecke weder zeichnet noch malt, sondern materielle Dreiecke
 anmalt und zusammenlegt, also handwerklich aktiv wird.)
anmalt und zusammenlegt, also handwerklich aktiv wird.)
(... woran im Hinblick auf die nachfolgenden Aufgaben immerhin schon bemerkenswert ist, dass es weniger blaue als rote Dreiecke gibt)

Genau genommen müssen die Schüler aber
Sie müssen "nur" wissen, was zu
![]() ist, nämlich 6 :
16 .
ist, nämlich 6 :
16 .
Man
muss hier also
 - und diesem sagen,
was er
- und diesem sagen,
was er 
Vermutlich wurde hier die 5. Reihe bewusst nicht
eingezeichnet, damit die Schüler sie sich überhaupt erst denken müssen.
Trotzdem hätte ich es nett gefunden, wenn unter der vierten Reihe Platz
für die 5. Reihe gelassen hätten, damit
die Schüler letztere auch zeichnen könnten:

(womit ein Nachteil von Tablets deutlich wird: man kann in vielen "Apps" nicht selbst zeichnen; und die Schüler sind immer gut beraten, wenn sie Buntstifte dabei haben).
Damit erhöht sich
und ergibt sich analog zur Frage 1 ein
prozentualer
Anteil von  .
.
Also nichts Neues unter der Sonne, außer ganz
OHNE ![]() , dass die 5. Reihe selbst gedacht bzw.
gezeichnet werden muss.
, dass die 5. Reihe selbst gedacht bzw.
gezeichnet werden muss.
Bzw. neu ist nur, dass der prozentuale Anteil von 37,5 % auf 40 % gestiegen ist.
... womit sich fast automatisch die (im eigentlichen Sinne mathematische) Frage stellt, was passiert, wenn immer mehr Reihen (also eine 6., 7., 8., ... 100., 1000., 100000... Reihe) hinzu kommen:

Wie bereits gesagt, beginnt hier überhaupt erst die
eigentliche Mathematik, und zwar OHNE ![]() .
.
Wenn die Schüler nicht gerade ohne jede mathematische Überlegung einfach auf gut Glück antworten (hier mit einer Trefferwahrscheinlichkeit von immerhin 50 %), bleibt ihnen gar nichts anderes, als ein allgemeines Gesetz zu finden, wie die Reihen aufgebaut sind.
(Einige Schüler haben solch ein Gesetz vielleicht schon bei Frage 2 entdeckt.)
Ein mögliches Vorgehen
(eine Aufgabe ist besonders gelungen, wenn es verschiedene [auch verschieden schwierige] Wege zum [selben] Glück gibt):

Es gibt also in jeder Reihe ein
blaues Dreieck weniger, als es rote
Dreiecke gibt. Deshalb liegt der prozentuale Anteil
der blauen Dreiecke an
allen Dreiecken garantiert
unter 50 % und ist die Antwort
auf Ahmeds Vermutung also  .
.
Ich habe die Aufgabe für mich allerdings anders und mit erheblich weniger Zeitaufwand gelöst, indem ich mir vor meinem inneren Auge eine Fortsetzung des Musters nach unten vorgestellt habe:

Das sieht auf den ersten Blick danach aus, dass
gleich viele blaue und
rote Dreiecke auftreten (50 %
blaue und 50 % rote)
, und deshalb scheint  richtig zu sein.
richtig zu sein.
Oder zwar weniger anschaulich und dennoch noch
einfacher: da sich die blauen und die roten Dreiecke in den Zeilen streng
abwechseln, sind in unteren und damit immer längeren Zeilen etwa gleich viele
blaue und rote Dreiecke vorhanden (50 %
blaue und 50 % rote), weshalb wieder  richtig zu sein scheint.
richtig zu sein scheint.
 .
.

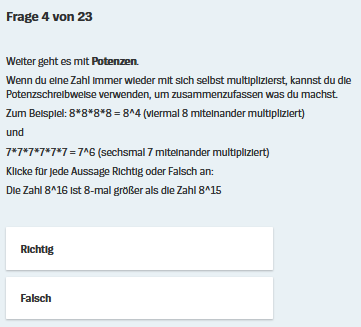
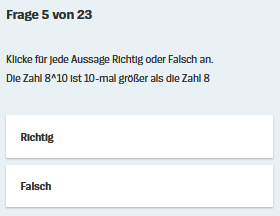
 verwendeten Potenzen an:
verwendeten Potenzen an:
 , dass 816
8-mal
größer als 815 ist.
, dass 816
8-mal
größer als 815 ist.
 .
.
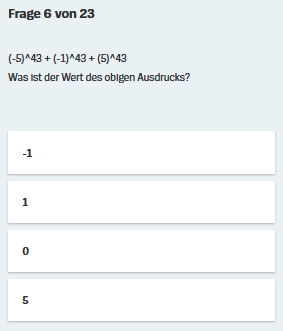
 (inkl. dem richtigen) sehr einfach sind.
(inkl. dem richtigen) sehr einfach sind. Oder kurz
(-5)43
+ (-1)43
+(5)43
=  .
.
Man muss
zur Lösung dieser Aufgabe also zwei Potenzregeln kennen und anwenden, aber
nicht rechnen können.

Vorweg zum rot unterstrichenen
Satz in der Aufgabenstellung
![]() :
:
wenn da von den "letzten Ziffern [Plural] der Zahl [Singular]" die Rede ist, stellt sich doch die (Doppel-)Frage,
welche einzelne Zahl da denn überhaupt gemeint ist
(die im vorletzten Satz genannte "Zahl 7"?),
wie viele "letzte[...] Ziffern" der einzelnen Zahl gemeint sind
(die letzten zwei, drei ... Ziffern?).
Gemeint sind aber wohl
die
Zahlen (Plural) rechts von den
Gleichheitszeichen, also
 ,
,
die (einzelne)
letzte Ziffer (Singular) jeder dieser Zahlen, also

(obwohl das
Spielchen auch mit den letzten beiden Ziffern
 funktioniert,
wenn man 7 als 07 schreibt).
funktioniert,
wenn man 7 als 07 schreibt).
In
![]() wird
deutlich, was Mathematik eigentlich ist:
wird
deutlich, was Mathematik eigentlich ist:
eben nicht Rechnen, das nur Handwerkszeug ist, sondern
(... eine Aussage, die viele Laien [Schüler] sehr erstaunen wird, da die Schule das üblicherweise nicht im mindesten vermittelt.)
Aber zurück zu
 →
→
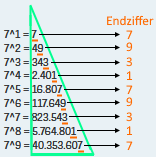 .
.
Wir vergessen jetzt mal für
eine Weile die komplizierten Potenzen und
beschäftigen uns vorerst nur mit der einfachen Zahlenliste
![]() , die hier aus
Platzgründen erstmal quergelegt wird:
, die hier aus
Platzgründen erstmal quergelegt wird:
![]()
Wenn man diese Liste mehrfach
von links nach rechts liest, wird sich schnell (wie bei Telefonnummern) ein
Rhythmus 
![]() einstellen
und damit das Muster
einstellen
und damit das Muster ![]()
![]() deutlich.
deutlich.
Oder fünf mal hintereinander:
![]() . Da wird
deutlich, dass z.B. an der 19. Stelle
eine 3 steht.
. Da wird
deutlich, dass z.B. an der 19. Stelle
eine 3 steht.
Hätten die Aufgabenautoren nicht nach 7190, sondern nach 719 gefragt, so könnten wir jetzt antworten: wenn man 719 ausrechnet, so hat das Ergebnis als letzte Ziffer eine 3 .
(Nebenbei: 719 ≈ 11398895185373100. Das ist - wohlgemerkt - nur eine vom Taschenrechner errechnete Näherung, denn wir wissen ja, dass die letzte Ziffer eine 3 sein müsste.)
Die Aufgabenautoren
wollten nun aber vermutlich das simple Abzählen, das ja noch ganz unmathematisch ist, unmöglich machen
und haben wohl deshalb den sehr hohen Exponenten 190 gewählt, bei dem man eine ewig lange Zahlenschlange niederschreiben und abzählen müsste und sich dabei vermutlich auch immer wieder vertun würde.
Für den Exponenten 190 würde die Zahlenschlange etwa so aussehen:
|
|
||||
|
|
|
Da fragt sich doch jeder anständige Mensch,
wie oft (= x)
das Viererpack
![]() bis zur
190. Stelle hintereinander passt. Das kann
man nun aber nicht mehr einfach abzählen, sondern muss man
wohl mal rechnen (?):
bis zur
190. Stelle hintereinander passt. Das kann
man nun aber nicht mehr einfach abzählen, sondern muss man
wohl mal rechnen (?):
4 • x = 190 | : 4
⇔
x = ![]()
Bevor das eigentliche Rechnen aber überhaupt erst
anfängt, hören wir damit schon wieder auf, füttern stattdessen ![]() mit
mit ![]() und
erhalten x =
47,5 . Das Viererpack
und
erhalten x =
47,5 . Das Viererpack
![]() passt also bis
zur 190. Stelle
47,5 mal hintereinander.
passt also bis
zur 190. Stelle
47,5 mal hintereinander.
Nehmen wir davon erstmal nur den ganzzahligen
Anteil 47, also die Anzahl der ganzen
![]() :
:
4 • 47 = 188, d.h.
|
47 Viererpacks à
|
|
|||
|
|
|
|
||
Um nun noch von der
188. zur 190. Stelle zu kommen,
müssen wir noch zwei Stellen bzw. 0,5 •
![]() =
=
![]() •
•
![]() =
=
![]() weiter nach rechts gehen:
weiter nach rechts gehen:
|
|
|
|||
|
|
|
|
||
An der 190.
Stelle steht also eine 9, und deshalb hat
die ausgerechnete Potenz 7190 als
letzte Ziffer die  .
.
(Noch drei interessante Anmerkungen, die hier aber nicht vertieft werden sollen, da das allzu weit vom eigentlichen Thema wegführen würde:
: ergibt sich nur bei der Basis 7 eine stetige Wiederholung derselben Endziffern?
: warum kommen bei der Basis 7 [nur] die Endziffern 7, 9, 3 und 1 vor?
: es ist doch allemal interessant, dass wir die Endziffer der ausgerechneten Zahl 7190 ermitteln können, ohne ansonsten irgendeine Ahnung von der Zahl zu haben
[dass z.B. 7190 ≈ 3 7036300802 8160000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000 0000000000].)
Zu Frage 8 - 15:  :
:

Es sei kurz darauf hingewiesen, dass vorweg Beispiele für "immer / manchmal / niemals wahr" gegeben werden.
Damit aber zur Kurzversion  :
:
Kleine Sprachkritik:
Man kann den Satz
"Ein 1,65 Meter großes 15-jährige Mädchen war zumindest einmal in ihrem Leben halb so groß wie momentan"
auf zwei Arten lesen:
"Ein BELIEBIGES 1,65 Meter großes 15-jährige Mädchen [bzw. JEDES 165 Meter große 15-jährige Mädchen] war zumindest einmal in ihrem Leben halb so groß wie momentan"
Dann bedeutet
"IMMER wahr": JEDES 1,65 Meter große 15-jährige Mädchen war zumindest einmal in ihrem Leben halb so groß wie momentan,
"MANCHMAL wahr": EINIGE 1,65 Meter große 15-jährige Mädchen waren zumindest einmal in ihrem Leben halb so groß wie momentan (und einige waren es nicht),
"NIEMALS wahr": KEIN 1,65 Meter großes 15-jährige Mädchen war zumindest einmal in ihrem Leben halb so groß wie momentan.
"Ein BESTIMMTES 1,65 Meter großes 15-jährige Mädchen [z.B. Erna Keinnamski aus Pusemuckel] war zumindest einmal in ihrem Leben halb so groß wie momentan".
Dann bedeutet
"IMMER wahr": Erna war IMMER halb so groß wie momentan,
"MANCHMAL wahr": Erna war MANCHMAL halb so groß wie momentan,
"NIEMALS wahr": Erna war NIEMALS halb so groß wie momentan.
Hier ist nun aber a. richtig, d.h. je nach Bedeutung von "Ein [...] Mädchen" kommen völlig unterschiedliche Lösungen der Aufgabe heraus. Arme Schüler!
Beim Vergleich mit der Version
"JEDER Mensch war zumindest einmal in seinem Leben halb so groß wie momentan"
erkennt man, wie informationsüberfrachtet die Behauptung
"Ein [beliebiges] 1,65 Meter großes 15-jährige Mädchen war zumindest einmal in ihrem Leben halb so groß wie momentan"
ist:
von den mathematischen (Zahlen-)Informationen ist "15-jährig[...]" überflüssig: es könnte genauso gut ein 14- oder 16-jähriges Mädchen sein, Hauptsache, es ist 1,65 Meter groß;
und nebensächlich ist auch, dass von einem Mädchen die Rede ist.
Bleiben die beiden anderen Zahlen:
zu "1,65 Meter":
angenommen mal, die Aufgabenautoren hätten nicht 1,65 Meter, sondern nur 0,65 Meter gewählt. Die Hälfte davon ist 0,325 Meter bzw. 32,5 cm, und so groß war ein Mensch höchstens als Embryo, den man natürlich auch schon als Leben betrachten kann, woran Schüler aber vermutlich kaum denken werden, da wir unsere Lebenszeit üblicherweise ab unserer Geburt rechnen.
Eine allgemeine Aufgabenstellung ohne die konkrete derzeitige Größe müsste also arg umständlich so lauten:
"JEDER Mensch, der mindestens doppelt so groß wie bei seiner Geburt ist, war zumindest einmal in seinem Leben halb so groß wie momentan."
Interessant an "1,65 Meter" ist auch, dass die Zahl 1,65 "krumm" ist, was beim Halbieren zu einer nicht ganz einfachen (aber dem Taschenrechner überlassenen) Rechnung führen würde und zudem einen noch "krummeren" Wert ergibt: 1,65 : 2 = 0,825.
Aber vielleicht haben die Aufgabenautoren ja bewusst die "krumme" Zahl 1,65 gewählt, damit Schüler erst gar nicht auf die Idee kommen, diese "krumme" Zahl zu halbieren, d.h. vielleicht wollten die Aufgabenautoren erreichen, dass die Schüler erst gar nicht auf die Idee kommen zu rechnen.
Ansonsten wurde "Ein 1,65 Meter großes 15-jährige Mädchen" von den Aufgabenautoren wohl gewählt, weil die Schüler, die bei PISA getestet werden, ca. 15 Jahre alt sind und die Größe 1,65 Meter da realistisch ist. Was für eine Lebensnähe also! - die den Schülern aber nicht im mindestens bei der Aufgabenlösung hilft.
Genauso gut hätten die Aufgabenautoren also schreiben können:
"Ein 1,35 Meter großer [also kleinwüchsiger] 98-jähriger Mann [...]."
zu "halb so groß":
es könnte genauso gut "drei Viertel so groß" oder "sieben Neuntel so groß" heißen. Am Lösungsweg würde das nichts ändern, vermutlich die Schüler aber gründlich verunsichern
("igitt, komplizierte Bruchrechnung", obwohl ja nicht gerechnet wird).
zu "mindestens einmal in ihrem Leben":
kein Mensch ist heute 1,64 cm und morgen urplötzlich (ohne Übergang) 1,65 cm groß
(wohl aber kann er in einem Wachstumsschub zwischen zwei Messungen über Nacht um 1 cm gewachsen sein).
Entscheidend für den Lösungsweg ist es daher, dass der Größengraph keine Sprünge aufweist, also ohne Absetzen mit einem einzigen durchgehenden Strich zu zeichnen ist.
Schauen wir uns also mal einen ersten (Teil-)Größengraphen an:
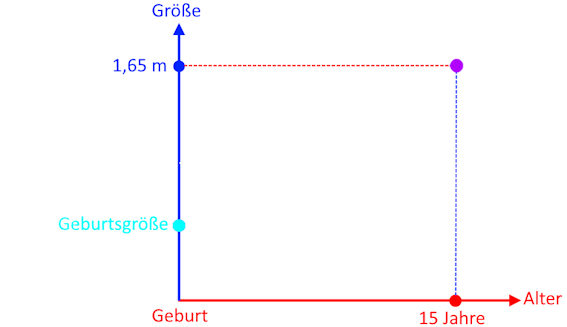
Gesucht ist nun eine
durchgehende Linie von
![]() nach
nach
![]() , die zeigt, wie sich die
Körpergröße im bisherigen Leben verändert hat.
, die zeigt, wie sich die
Körpergröße im bisherigen Leben verändert hat.
Ein Beispiel ist da
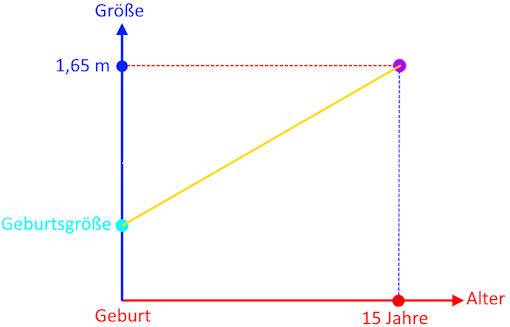 .
.
Wenn wir nun zusätzlich noch die "Halbe-Größe-Linie" einzeichnen, ergibt sich
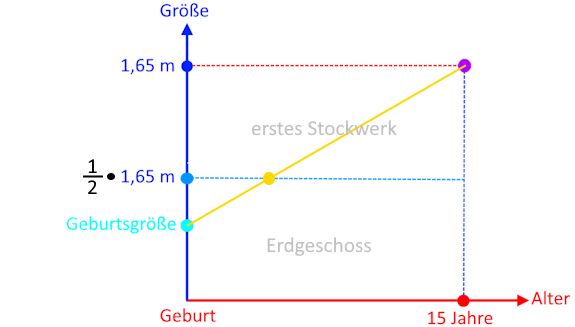
Weil die durchgehende Linie die "Halbe-Größe-Linie" durchgehend ist, schneidet sie die
(hier zur besseren Unterscheidbarkeit gestrichelt gezeichnete, in Wirklichkeit aber ebenfalls durchgehende)
"Halbe-Größe-Linie"
GARANTIERT in einem Punkt, und zwar in
![]()
(wenn die
durchgehende Linie vom Erdgeschoss ins erste
Stockwerk will, muss sie irgendwo [in einem Punkt
![]() ] durch die
Decke gehen).
] durch die
Decke gehen).
Das war der Fall, als das Kind ca. 4 Jahre alt war:
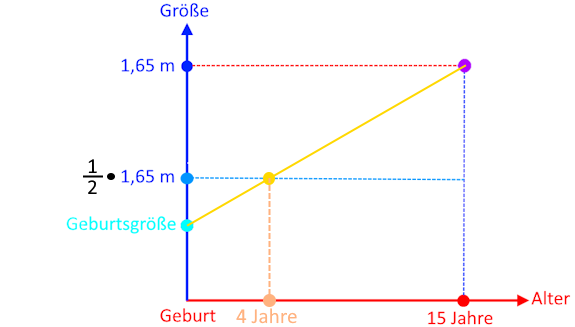
Weil Kinder/Jugendliche aber vor allem in der Pubertät rasant wachsen, ist wohl realistischer:

Damit nun aber endlich
(wieder) zu "mindestens einmal in ihrem Leben", also "eventuell auch
mehrfach (zwei-, drei-, viermal ...)". Die
durchgezogene Linie hat also mehrere (zwei, drei, vier ...) Punkte
![]() mit der "Halbe-Größe-Linie"
gemeinsam.
mit der "Halbe-Größe-Linie"
gemeinsam.
Beispiel A:

(die durchgezogene Linie kommt immer aus dem Erdgeschoss, wechselt mehrfach zwischen ersten Stock und dem Erdgeschoss, endet aber immer im ersten Stock);
Mal abgesehen davon,
dass bei dem Graphen die Ausschläge nach oben oder unten zwecks besserer
Erkennbarkeit übertrieben wurden: in unserem Anwendungsfall "Körperwachstum"
wichtiger ist, dass der Mensch, um den es hier geht, abwechselnd
größer
![]() und
kleiner
und
kleiner
![]() wird. Das ist
zwar mathematisch schön schwungvoll, im Anwendungsfall allerdings Blödsinn.
wird. Das ist
zwar mathematisch schön schwungvoll, im Anwendungsfall allerdings Blödsinn.
Beispiel B:

Hier verläuft die durchgezogene Linie zwischen den Punkten P1 und P2 auf der "Halbe-Größe-Linie" , d.h. die Person bleibt einige Zeit (im Zeitintervall G) gleich groß. Das ist durchaus realistisch, da Menschen bekanntermaßen oftmals in Wachstumsschüben wachsen.
Die Aufgabenautoren wollten mit "mindestens einmal in ihrem Leben" also vermutlich diesen möglichen Spezialfall berücksichtigen.
Aber da geht die mathematische Exaktheit auf Kosten der Verständlichkeit.
Zudem wird hier schön ein Unterschied zwischen Alltags- und mathematischer Fachsprache deutlich:
für Mathematiker besteht
die (eine) Strecke
![]() aus
unendlich vielen Punkten (was in "mindestens einmal" enthalten ist),
d.h. die Person ist unendlich oft (mehr als einmal) gleich groß;
aus
unendlich vielen Punkten (was in "mindestens einmal" enthalten ist),
d.h. die Person ist unendlich oft (mehr als einmal) gleich groß;
für Laien ist dieses
"unendlich oft [...] gleich groß" aber geradezu widersinnig, denn für sie
kann ein Mensch in seinem kurzen Leben nicht unendlich oft eine Eigenschaft
haben. Für Laien verweist die (eine) Strecke
![]() vielmehr
auf ein Zeitintervall G : die Person ist
während dieses (einen) Zeitintervalls, also ein (einziges) Mal gleich alt.
Und Laien interessieren sich nicht dafür, woraus (aus wie vielen
Augenblicken) ein ausgedehntes Zeitintervall besteht. Für sie ist der
Augenblick nicht Teil eines Intervalls (Zeitraums),
sondern das Gegenteil eines Intervalls.
vielmehr
auf ein Zeitintervall G : die Person ist
während dieses (einen) Zeitintervalls, also ein (einziges) Mal gleich alt.
Und Laien interessieren sich nicht dafür, woraus (aus wie vielen
Augenblicken) ein ausgedehntes Zeitintervall besteht. Für sie ist der
Augenblick nicht Teil eines Intervalls (Zeitraums),
sondern das Gegenteil eines Intervalls.
(Nebenbei: was ist eigentlich ein "Augenblick":
 oder
oder
 ?)
?)
Ein Laie würde wohl "ich bin eine Woche in Urlaub" sagen, aber niemals "ich bin eine Woche à 7 Tage à 24 Stunden à 60 Minuten à 60 Sekunden à 1000 Millisekunden ... in Urlaub": für einen Laien ist die Zeit
sämig
 (dickflüssig,
"stetig"),
(dickflüssig,
"stetig"),
nicht körnig
 (in der
mathematischen Fachsprache "diskret", nicht zu verwechseln mit
alltagssprachlich "diskret = vertraulich, rücksichtsvoll").
(in der
mathematischen Fachsprache "diskret", nicht zu verwechseln mit
alltagssprachlich "diskret = vertraulich, rücksichtsvoll").
(Die Frage, ob die Zeit
"sämig" oder "körnig" ist, beschäftigt durchaus auch Wissenschaftler [Physiker]:
![]() .)
.)
Dabei hat nicht der Mathematiker mehr recht (bzw. die einzige Wahrheit) als der Laie, sondern beide haben nur unterschiedliche Perspektiven auf dasselbe (viele Punkte / ein Intervall).
Deshalb hätte ich in der Aufgabenstellung einfach nur "mal" statt "zumindest einmal in ihrem Leben" geschrieben.
Vielleicht war die Informationsüberfrachtung aber Absicht der Aufgabenautoren, weil sie herausfinden wollten, ob Schüler (wie so oft bei Textaufgaben nötig) überschüssige Informationen rausfiltern konnten.
(Nebenbei:
ich bin mir nicht sicher, dass alle Schüler [mit "Migrationshintergrund"] das Wort "momentan" verstehen; da hätte ein "jetzt" gereicht;
"mindestens" scheint mir für heutige Schüler auch verständlicher als "zumindest" zu sein,
ich würde auch nicht fragen, ob etwas "niemals" wahr ist, sondern ob es "nie" wahr ist.
Wer jetzt einwendet, dass die Schüler von heute [doch nicht] so doof sind, "momentan", "zumindest" und "niemals" nicht zu verstehen, hat nur noch nicht begriffen, dass sich die Sprache seit seiner Jugend und schon immer verändert hat.
Und überhaupt: wer die Maßstäbe seiner Jugend unreflektiert an die heutige Jugend anlegt, hätte unter keinen Umständen Lehrer werden dürfen.
Zuguterletzt sei hier noch erwähnt, dass auch das Wort "manchmal" in "manchmal wahr" problematisch ist. Vgl. etwa
da klingt doch mit, dass
etwas nur in seltenen Ausnahmefällen wahr,
in den meisten Fällen jedoch falsch
ist: ![]()
Mathematiker meinen mit
"manchmal wahr" aber sogar solche Fälle, in denen etwas in fast allen
Fällen wahr ist. Der Haken ist da das
Wörtchen "fast", das im Extremfall bedeuten kann, dass etwas nur in einem
einzigen Fall falsch ist:
![]()
In der Alltagssprache, nicht aber in der Mathematik wäre also noch die vierte Kategorie "IN DEN MEISTEN FÄLLEN wahr" nötig. Aber ein Schüler, dem diese Antwortmöglichkeit nicht mitgegeben wird, läuft Gefahr, falsch zu antworten oder gar nicht antworten zu können.
Nun hat ein Schüler in der
PISA-Prüfung gar nicht die Zeit, so umständliche Überlegungen anzustellen wie
ich mit meinen "Größengraphen", ja, ich bezweifle, dass er überhaupt an
mathematische Graphen denkt. Sondern er wird eher an einen "sämigen" (s.o.)
Verlauf der Körpergröße denken: wenn ein Mensch bei Geburt 0,5 m groß ist und
mit 15 Jahren 1,65 m, wächst er irgendwann durch die Hälfte von 1,65 m
hindurch:  .
.
(Schüler müssen ja nicht meine Vorgehensweisen wählen [Größengraph, das Stockwerk wechseln, wachsende Pflanze ...], aber man sollte ihnen doch "beibringen", [wenn irgend möglich] Analogien zu alltäglichen Erlebnissen und Vorgängen zu nutzen.
Dasselbe gilt - nebenbei - auch beim Verständnis von Literatur.)
Ich habe die "Größengraphen" ja nur benutzt, um zu zeigen, wie den Aufgabenautoren der allzu umständliche Ausdruck "zumindest einmal in ihrem Leben" in die Aufgabe gerutscht sein mag.

Einfacher (?) gefragt: ist es IMMER / (nur) MANCHMAL´/ NIEMALS wahr, dass die Körpergröße vom Alter abhängt?
Spontan werden da die meisten doch wohl antworten,
dass das EINDEUTIG FALSCH, also NIEMALS wahr ist
(man denkt zu allerletzt an seltene
Ausnahmen, es sei denn, man hat mal eine eindrücklich miterlebt; dass
es also z.B. durchaus
![]() blonde Türken
blonde Türken  gibt
und somit "Türken = schwarzhaarig" nur ein [wenn auch verständliches] Vorurteil
ist).
gibt
und somit "Türken = schwarzhaarig" nur ein [wenn auch verständliches] Vorurteil
ist).
Konstruieren wir also mal gezielt ein extremes Beispiel: "Ein 18-jähriges Mädchen [also eine erwachsene Frau] ist größer als ein eine Woche altes Mädchen [also ein Baby]." Das ist zweifelsohne IMMER wahr
(und zwar sogar dann, wenn die 20-jährige kleinwüchsig ist).
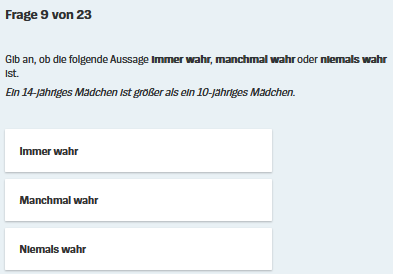
In welche Kategorie gehört nun aber "Ein 14-jähriges Mädchen ist größer als ein 10-jähriges Mädchen"?:
IMMER wahr,
NIEMALS wahr
oder vielleicht sogar MANCHMAL wahr?
"Ein 14-jähriges Mädchen ist größer als ein 10-jähriges Mädchen" ist "IN DER REGEL bzw. MEISTENS wahr", da Menschen in der Jugend (zwischen dem 10. und 14. Lebensjahr) noch wachsen.
Aber die REGEL kann Ausnahmen haben bzw. "MEISTENS" bedeutet keineswegs "immer".
(Von Vorteil ist es hier wieder, wenn man [ohne alle Mathematik]) konkrete eigene Erlebnisse nutzen kann. So war z.B. mein jüngerer Bruder lange Zeit für sein Alter viel zu klein [und hat sehr darunter gelitten]. Aber mit ca. 17 Jahren hat er einen riesigen Schuss nach oben gemacht - und ist seitdem 10 cm größer als ich.)
Es fällt allerdings schwer, "IN DER REGEL bzw.
MEISTENS wahr" mit der Kategorie
 gleichzusetzen, da
gleichzusetzen, da
"manchmal" in der Alltagssprache "in
wenigen Fällen" bedeutet
![]()
und eben nicht "IN DER REGEL bzw.
MEISTENS" ![]() .
.
Vor allem aber: bei der Lösung der Aufgabe wird niemals gerechnet, und zwar auch nicht mit den beiden einzigen in der Aufgabe enthaltenen Informationen, nämlich 14 und 10. Oder genauer: das einzig Wichtige an diesen Zahlen ist, dass 14 größer als 10 ist, was intuitiv klar ist und nicht erstmal errechnet werden muss.
Wichtig an der Aufgabe ist, dass die Schüler hier (wieder) dynamisch denken müssen, da 10- und 14-jährige noch in der Wachstumsphase sind. Alles wäre viel einfacher, wenn die beiden Vergleichskandidatinnen schon aus der Wachstumsphase heraus wären, die Aufgabe als z.B. "Eine 34-jährige Frau ist größer als ein 30-jährige Frau" lauten würde, was wieder "MANCHMAL" der Fall ist,
solange man darunter (besser formuliert) "34-jährige Frauen sind größer als 30-jährige Frauen" versteht
und nicht "Eine [bestimmte] 34-jährige Frau [Erna N.] ist größer als eine [bestimmte] 30-jährige Frau [Petronella M.]"
(wast dann IMMER oder NIEMALS wahr ist).

Unter den  geht es hier zum ersten Mal
geht es hier zum ersten Mal
nicht mehr um die Außenwelt (Körpergrößen),
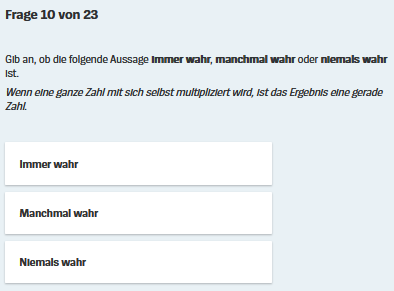
sondern um innermathematische Zusammenhänge (hier Quadrieren).
Weil in der Aufgabenstellung von "geraden" Zahlen die Rede ist, erkennen einige Schüler vielleicht sofort, dass es günstig sein könnte, die Behauptung mal mit geraden und ungeraden Zahlen auszuprobieren.
Wenn man hingegen von nix 'ne Ahnung hat, überhebe man sich nicht und fange man mit ganz einfachen Zahlen an
(auch, um gar nicht rechnen zu müssen oder nur ganz einfache Rechnungen durchführen zu müssen!):
1 • 1 = 1 . Das Ergebnis ist also ungerade, womit schon die Behauptung, dass das Quadrat einer ganzen Zahl IMMER gerade ist, in Trümmern liegt.
2 • 2 = 4 . Das Ergebnis ist also gerade, womit sofort auch die Behauptung, dass das Quadrat einer ganzen Zahl NIEMALS gerade ist, in Trümmern liegt.
Bleibt also nur
 .
.
Es reichen also zwei (Mini-)"Rechnungen", und deshalb müssen Schüler auch gar nicht daran denken, dass zu den "ganzen" Zahlen ja eigntlich auch die negativen ganzen Zahlen (-1, -2, -3 ...) gehören
(die, wenn man sie mit sich selbst multipliziert, ohnehin doch wieder positive ganze, also "natürliche" [gerade oder ungerade] Zahlen ergeben).

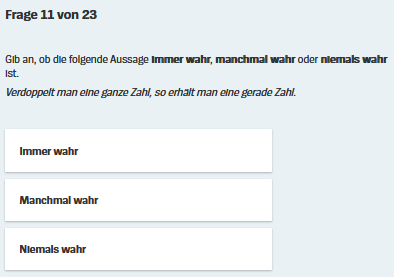
Wenn in der Aufgabe vorher
 heraus kam, folgen
jetzt doch wohl so sicher wie das Amen in der Kirche "IMMER wahr" oder "NIEMALS
wahr"!
heraus kam, folgen
jetzt doch wohl so sicher wie das Amen in der Kirche "IMMER wahr" oder "NIEMALS
wahr"!
Wieder mit besonders einfachen ganzen Zahlen:
2 • 1 = 2 . Das Ergebnis ist also gerade, womit die Behauptung, dass eine verdoppelte ganze Zahl IMMER gerade ist, bestätigt wird.
2 • 2 = 4 . Das Ergebnis ist ebenfalls gerade, womit die Behauptung, dass eine verdoppelte ganze Zahl IMMER gerade ist, nochmals bestätigt wird.
Da würde ich Schülern empfehlen, wegen des Zeitdrucks in der Prüfung ohne
weitere Überprüfungen und Überlegungen sofort
 anzustreichen
anzustreichen
(auf die Gefahr hin, dass es vielleicht doch noch Ausnahmen gibt und deshalb nur
 gilt;
gilt;
in
Wirklichkeit gibt es allerdings keine Ausnahmen, gilt also tatsächlich
 ).
).
Wenn aber
"eine ganze Zahl mit sich selbst multipliziert
ergibt eine gerade Zahl"
 ist und
ist und
"eine verdoppelte ganze Zahl ergibt eine
gerade Zahl"  ist,
ist,
können "Mit-Sich-Selbst-Multiplizieren [= Quadieren]" und "Verdoppeln nicht dasselbe sein.
Mit den Fragen 10 und 11 spielen die Aufgabenautoren also indirekt auf einen beliebten Schülerfehler an, nämlich x2 = x • 2. In der Regel ist nämlich x2 ≠ x • 2
(einzige Ausnahmen: 02 = 0 • 2 , 22 = 2 • 2 ).
Und gleichzeitig verhindern die Aufgabenautoren den beliebten Schülerfehler, indem sie in Aufgabe 10 nicht von "Quadrieren", sondern von "mit sich selbst malnehmen" ( ≠ mit 2 malnehmen) sprechen.

Weil in Aufgabe 10
 und in Aufgabe 11
und in Aufgabe 11
 richtig wahr, könnte
man vermuten, dass die Aufgabenautoren alle Möglichkeiten abprüfen und deshalb
nun in Aufgabe 12
richtig wahr, könnte
man vermuten, dass die Aufgabenautoren alle Möglichkeiten abprüfen und deshalb
nun in Aufgabe 12  dran ist. Wer auf solche Logik vertraut, überlegt also eventuell gar nicht
weiter, sondern hakt einfach
dran ist. Wer auf solche Logik vertraut, überlegt also eventuell gar nicht
weiter, sondern hakt einfach
 ab ("wird schon
stimmen").
ab ("wird schon
stimmen").
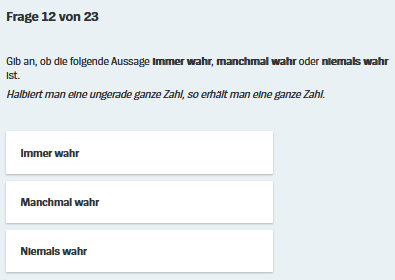
Man könnte hier aber auch eine Falle vermuten und doch lieber nochmals selbst nachdenken.
Wir fangen wieder mit möglichst einfachen, diesmal ungeraden ganzen Zahlen an:
1
: 2
= ![]() bzw. für
Bruchlegastheniker und Rechenanalphabeten mit
bzw. für
Bruchlegastheniker und Rechenanalphabeten mit ![]() 1 :
2 = 0,5 , und das ist keine
ganze Zahl;
1 :
2 = 0,5 , und das ist keine
ganze Zahl;
3
: 2
= ![]() bzw. für
Bruchlegastheniker und Rechenanalphabeten mit
bzw. für
Bruchlegastheniker und Rechenanalphabeten mit ![]() 3 :
2 = 1,5 , und das ist wieder keine
ganze Zahl.
3 :
2 = 1,5 , und das ist wieder keine
ganze Zahl.
Weil wir faul sind und keine Zeit haben, kreuzen
wir also (wie zu erwarten; s.o.)
 an, was tatsächlich
auch allgemein richtig ist.
an, was tatsächlich
auch allgemein richtig ist.
Schüler werden es kaum bemerken, aber Frage 12 ist im Grunde die "Gegenfrage" zu Frage 11, d.h. die Aufgabenautoren prüfen hier ganz systematisch ab.
Insgesamt prüfen die Fragen 10, 11 und 12 die einfachsten innermathematischen Beispiele für "IMMER / MANCHMAL / NIEMALS" ab, d.h. der nächste PISA-Test kann eigentlich nur schwieriger werden.

Hier wird tatsächlich mal der typisch deutsche Mathematikunterricht abgeprüft, d.h. Termumformungen9 (und später dann Gleichungslösen17 ), also Patentrezepte anwenden und Rechnen!).
Schöner als 3x+1 = (6x+2)/2 ist natürlich
![]() . Hier muss man nun die
Möglichkeit erkennen, zwei mathematische Rechenregeln anzuwenden. Fangen wir mit
dem schwierigeren
. Hier muss man nun die
Möglichkeit erkennen, zwei mathematische Rechenregeln anzuwenden. Fangen wir mit
dem schwierigeren ![]() an, um
zu sehen, ob sich daraus das einfachere 3x + 1 machen lässt.
an, um
zu sehen, ob sich daraus das einfachere 3x + 1 machen lässt.
Dabei ist es natürlich günstig, wenn man sofort erkennt, dass 6x + 2 das Doppelte von 3x + 1 ist, weil nach dem Distributivgesetz gilt: 6x + 2 = 2 • 3x + 2 • 1= 2 • (3x + 1) oder kurz 6x + 2 = 2 • (3x + 1) .
(Das einzige Rechnen besteht hier also in
6 : 2 = 3 und 2 : 2 = 1. Japanischen Schülern soll das sogar schon ohne ![]() gelungen sein.)
gelungen sein.)
Es folgt also
![]() =
=
![]() . Da kommt im Zähler und
im Nenner eine 2 vor, und außerdem wird im
Zähler mit 2 multipliziert, weshalb wir den
Bruch durch 2 kürzen können:
. Da kommt im Zähler und
im Nenner eine 2 vor, und außerdem wird im
Zähler mit 2 multipliziert, weshalb wir den
Bruch durch 2 kürzen können:
![]() =
=
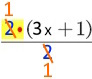 =
=
![]() = 3x + 1 .
= 3x + 1 .
Insgesamt also
![]() =
=
![]() =
=
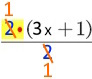 =
=
![]() = 3x + 1
= 3x + 1
oder kurz
![]() =
3x + 1 .
=
3x + 1 .
Das ist für alle x richtig, also
 .
.

Wenn die Originalaufgabe so aussah
(und nicht erst im "Spiegel" so vermurkst wurde),
haben die Aufgabenautoren sofort für drei unnötige Schwierigkeiten gesorgt:
: was bedeuten die Querstriche in
 ?
?
ich vermute, dass damit angedeutet werden soll,
dass die mit Querstrichen versehenen Strecken beliebig lang sein dürfen
(allerdings nicht gleichgroß wie die jeweils
parallelen Ausschnittseiten
 oder kleiner,
weil dann ein Ausschneiden gar nicht möglich ist),
oder kleiner,
weil dann ein Ausschneiden gar nicht möglich ist),
dass also unendlich viele Anfangsrechtecke möglich sind
(z.B. das Original
 oder
oder
 oder
oder
 )
)
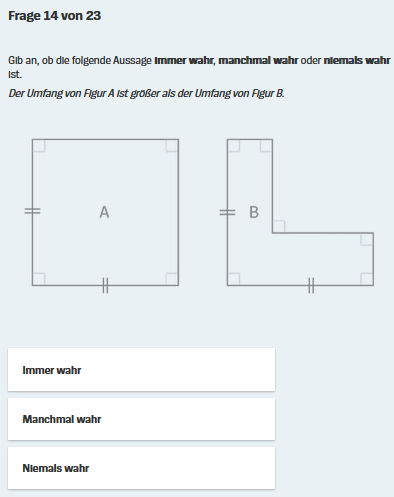
und sich damit überhaupt erst die Frage stellt, ob die Aussage "Der Umfang von Figur A ist größer als der Umfang von Figur B"
IMMER (für alle der unendlich vielen möglichen Anfangsrechtecke),
MANCHMAL (für einige Anfangsrechtecke und für einige nicht),
NIEMALS (für kein einziges Anfangsrechteck)
wahr (richtig, zutreffend) ist.
Nebenbei: auf den ersten Blick sieht es so aus,
dass die Aufgabenautoren sowohl bei der Ausgangsfigur
 als auch beim
Ausschnitt
als auch beim
Ausschnitt 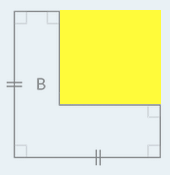 nicht ganz
allgemein Rechtecke, sondern Quadrate gemeint haben. Wenn man aber nachmisst,
nicht ganz
allgemein Rechtecke, sondern Quadrate gemeint haben. Wenn man aber nachmisst,
ist zwar die Ausgangsfigur
 quadratisch
quadratisch
nicht aber der Ausschnitt
 .
.
Glücklicherweise spielt es aber bei der Lösung der Aufgabe keine Rolle, ob
alle (auch nicht-quadratische) rechteckigen Ausgangsfiguren und ein nicht-quadratischer rechteckiger Ausschnitt gemeint war,
nur quadratische Ausgangsfiguren, aber ein (auch nicht-quadratischer) Ausschnitt
oder nur quadratische Ausgangsfiguren und ein quadratische Ausschnitte.
Nun habe ich gerade immer
im Plural von vielen (rechteckigen oder quadratischen) Ausgangsfiguren gesprochen,
hingegen im Singular von einem einzigen (rechteckigen oder quadratischen) Ausschnitt.
Grund dafür ist, dass die linke und untere Seite des Ausschnitts nicht mit Querstrichen versehen sind, der Ausschnitt als (wenn meine Deutung der Querstriche stimmt) nie verändert wird:
aus unterschiedlich großen Ausgangsfiguren
wird immer derselbe Ausschnitt ausgeschnitten.
An fast allen Ecken der beiden Figuren in der
Aufgabenstellung tauchen merkwürdige kleine Symbole auf:
 . Was da in der
Form
. Was da in der
Form ![]() daherkommt,
wird an deutschen Schulen meistens so
daherkommt,
wird an deutschen Schulen meistens so
![]() markiert und
bedeutet "rechter Winkel".
markiert und
bedeutet "rechter Winkel".
(
![]() scheint im
englischsprachigen,
scheint im
englischsprachigen, ![]() im deutschsprachigen Raum üblich zu sein.)
im deutschsprachigen Raum üblich zu sein.)
Es könnte also sein, dass den Schülern das Symbol
![]() im PISA-Test zum
ersten Mal begegnet. Für deutsche Schüler wäre also eine Sonderversion mit dem
Symbol
im PISA-Test zum
ersten Mal begegnet. Für deutsche Schüler wäre also eine Sonderversion mit dem
Symbol ![]() nötig.
nötig.
Aber vielleicht ist das Fehlen der deutschen
Version eine lässliche Sünde, weil die beiden Figuren
 sowieso an allen
Ecken und Enden rechtwinklig sind.
sowieso an allen
Ecken und Enden rechtwinklig sind.
Das war auch der Grund, weshalb ich schon oben andauernd von Rechtecken und Quadraten gesprochen habe.
(Unerwähnt bleibt in der Aufgabenstellung, dass "das Ganze" sowieso nur für rechtwinklige Figuren funktioniert; s.u. beim "Broadway".)
scheint mir die Behauptung "Der Umfang von Figur A ist größer als der Umfang von Figur B" in der Aufgabenstellung
(wie schon bei anderen Aufgaben oben)
zweifelhaft: die Schüler könnten doch wirklich
denken, dass mit Figur A und Figur B nur die beiden Figuren in
 gemeint sind - und
gemeint sind - und
(insbesondere auch wegen 1.)
völlig übersehen, dass auch unendlich viele andere Fälle gemeint sind.
Wenn aber nur die beiden Figuren in
 gemeint sind, sind
die sich immer auf viele Fälle beziehenden Antworten "IMMER / MANCHMAL / NIEMALS
wahr" sinnlos.
gemeint sind, sind
die sich immer auf viele Fälle beziehenden Antworten "IMMER / MANCHMAL / NIEMALS
wahr" sinnlos.
(Kurz eingeschoben seien Vermutungen dazu, wie die Aufgabenautoren
zu der Behauptung "Der Umfang von Figur A ist größer als der Umfang von Figur B" gekommen sein mögen,
weshalb sie die Frage 14 überhaupt in den Test aufgenommen haben
und weshalb die Behauptung "Der Umfang von Figur A ist größer als der Umfang von Figur B" so überzeugend (und doch falsch) ist:
Da in
 die Figur B
dadurch entsteht, dass aus der Figur A etwas ausgeschnitten wird, ist natürlich
die FLÄCHE von Figur A größer als die FLÄCHE von Figur B. Da liegt es doch
erstmal nahe zu glauben, dass es sich beim UMFANG wohl genauso verhält:
wenn eine FLÄCHE größer ist, ist auch ihr UMFANG größer
die Figur B
dadurch entsteht, dass aus der Figur A etwas ausgeschnitten wird, ist natürlich
die FLÄCHE von Figur A größer als die FLÄCHE von Figur B. Da liegt es doch
erstmal nahe zu glauben, dass es sich beim UMFANG wohl genauso verhält:
wenn eine FLÄCHE größer ist, ist auch ihr UMFANG größer
[vgl. etwa: ein [flächenmäßig] größerer Kreis hat such einen größeren Umfang].
Nebenbei: wie z.B. anhand von
 deutlich wird,
hat die Figur
deutlich wird,
hat die Figur  sogar
eine kleinere FLÄCHE und dennoch einen erheblich größeren
UMFANG als die Figur
sogar
eine kleinere FLÄCHE und dennoch einen erheblich größeren
UMFANG als die Figur
 .
.
Die Entkopplung von Fläche und Umfang bzw. im Dreidimensionalen von Volumen und Oberfläche ist ein entscheidendes Konstruktionsprinzip in Natur und Technik, um auf kleinem Raum dennoch eine möglichst große Oberfläche zu erhalten:
 [Naturschwamm],
[Naturschwamm],
[aufgeschnittener
Autokatalysator])
Nun aber zur Aufgabenlösung:
entscheidend sind die Erkenntnisse, dass
die Figuren rundweg rechtwinklig sind,
Figur B genauso hoch ist wie Figur A (was durch die Zeichnung ja nahegelegt wird)
und Figur B wohl auch genauso breit "gemeint" ist wie Figur A.
Hier sei nur die (wie ich finde) schönste, vielleicht intelligenteste, allemal aber kürzeste und deshalb / dennoch verständlichste Lösung vorgeführt:
wir markieren
in rot alles, was der die Außenstrecken von Figur A und von Figur B gemeinsam haben
und in hell/-dunkelblau und hell-/dunkelgrün, was sie (auf den ersten Blick) unterscheidet:

Und nun betrachten wir nur noch die Unterschiede, also

Wegen der rechtwinkligen Schnitte ist nun aber
die dunkelblaue Strecke in Figur A genauso lang wie die hellblaue Strecke in Figur B,
die dunkelgrüne Strecke in Figur A genauso lang wie die hellgrüne Strecke in Figur B,
d.h. auch in
 ergibt sich im Hinblick
auf den Umfang kein Unterschied zwischen den beiden Figuren.
ergibt sich im Hinblick
auf den Umfang kein Unterschied zwischen den beiden Figuren.
Daraus folgt:
die Behauptung "Der Umfang von Figur A ist
GENAUSO GROSS wie der Umfang von Figur B" ist
 ,
,
also ist die Behauptung "Der Umfang von Figur
A ist GRÖSSER als der Umfang von Figur B" aus der Aufgabenstellung
 .
.
Im Hinblick auf mein Zentralthema "[nicht] Rechnen" gilt hier bei Frage 14., dass da nichtmal ansatzweise gerechnet wird
(was sich bei Thema 4. Frage 16 - 20:
![]()
 fortsetzt; s.u.).
fortsetzt; s.u.).
Ich hatte oben mehrfach von einem "Ausschnitt"
bzw. "ausschneiden" gesprochen, obwohl davon in der PISA-Aufgabe nie die Rede
war: in  sind
die beiden Figuren A und B nur "irgendwie unterschiedlich", aber es bleibt
unklar, dass die Figur B aus der Figur A entstanden sein könnte. Es fehlt also
der "missing link" zwischen Figur A und Figur B.
sind
die beiden Figuren A und B nur "irgendwie unterschiedlich", aber es bleibt
unklar, dass die Figur B aus der Figur A entstanden sein könnte. Es fehlt also
der "missing link" zwischen Figur A und Figur B.
Das ist vermutlich Absicht gewesen: die Schüler sollten diesen "missing link" wohl überhaupt erst selbst entdecken.
Mit diesem "[dann nicht mehr] missing link" wird allerdings alles viel einfacher:
"Aus einer rechteckigen Figur A wird oben rechts ein kleineres Rechteck ausgeschnitten, wodurch die Figur B entsteht."
(Hier sei mal davon ausgegangen, dass sie
Schüler, wenn sie die beiden Figuren zeichnen, Rechteck A nicht so
 legen werden und dass
deshalb weitere Missverständnisse ausgeschlossen sind.)
legen werden und dass
deshalb weitere Missverständnisse ausgeschlossen sind.)
Wenn derart durch Ausschneiden Figur B aus Figur A entsteht, impliziert das, dass beide Figuren (trotz Ausschneidens) dieselbe Breite und Höhe haben
(und nicht, wie in
 , beim ersten
Hinsehen nur ungefähr dieselbe Breite).
, beim ersten
Hinsehen nur ungefähr dieselbe Breite).
Am besten wäre es natürlich, wenn die Schüler mittels Schere selbst schneiden würden. Da das aber in der PISA-Prüfung aber kaum möglich ist
(bzw. warum eigentlich nicht?),
könnte eine kleine Geschichte wirklich mal nicht schaden: Ahmed schneidet - und die Schüler können sich mit ihm identifizieren, also fiktiv mitschneiden.
In einer anderen Geschichte zum selben Thema wird nicht geschnitten, sondern gegangen:

Diese Aufgabe gilt nun offensichtlich als
Vorausdeutung auf das übernächste Thema "Wahrscheinlichkeitsrechnung", also 5. Frage 21 - 23:
 (s.u.).
(s.u.).

Mit der Behauptung
"Wird eine Münze 50-mal geworfen, so wird sie 25-mal mit dem Kopf nach oben landen"
eine fundamentale Erkenntnis der Wahrscheinlichkeitsrechnung abgeprüft.
Die Behauptung "Wird eine Münze 50-mal geworfen, so wird sie 25-mal mit dem Kopf nach oben landen" mogelt auf hinterhältige Weise die Wahrscheinlichkeit erst hinein und dann doch wieder heraus:
in der Behauptung wird die Zahl
![]() zwar nicht
explizit genannt, aber doch auf sie angespielt, denn 25 =
zwar nicht
explizit genannt, aber doch auf sie angespielt, denn 25 =
![]() • 50 ;
• 50 ;
weil aber 25 =
![]() • 50
zweifelsfrei richtig ist, wird suggeriert, dass auch die
Behauptung richtig ist;
• 50
zweifelsfrei richtig ist, wird suggeriert, dass auch die
Behauptung richtig ist;
gerade einem Schüler, der bei
![]() an die "[binomiale]
Gleichwahrscheinlichkeit" denkt, wird also suggeriert, dass die
Behauptung
an die "[binomiale]
Gleichwahrscheinlichkeit" denkt, wird also suggeriert, dass die
Behauptung
(in der raffinierterweise gar keine Wahrscheinlichkeit vorkommt)
IMMER wahr ist.
Es gibt gute Gründe dafür, dass die Mathematiker auch dann von "Wahrscheinlichkeit" sprechen, wenn etwas sicher ist
(was doch eigentlich ein Widerspruch in sich ist):
wenn ein Ereignis garantiert eintritt, sprechen sie von der Wahrscheinlichkeit 1 (100 %),
wenn ein Ereignis garantiert nicht eintritt, sprechen sie von der Wahrscheinlichkeit 0 (0 %).
Für Schüler wäre es vermutlich viel einfacher, wenn Sicheres nicht als "wahrscheinlich" bezeichnet würde. Denn dann könnte man die allgemeine Regel aufstellen:
"wenn etwas wahrscheinlich ist, ist es garantiert nicht sicher".
Im hier vorliegenden Fall:
eine Münze kann auf jede ihrer beiden Seiten fallen,
d.h. es liegt echte Wahrscheinlichkeit vor (mathematisch gesagt: die Wahrscheinlichkeit ist weder 0 noch 1)
und deshalb
kann die Münze zwar tatsächlich "25-mal mit dem Kopf nach oben landen"
aber die Münze wird nicht mit Sicherheit exakt "25-mal mit dem Kopf nach oben landen"
(sondern sie kann z.B. auch
50 mal mit dem Kopf und kein einziges Mal mit der Zahl nach oben fallen
oder 17 mal mit dem Kopf nach oben und 50 - 17 = 33 mal mit der Zahl nach oben,
[und das außerdem in vielen verschiedenen Reihenfolgen]).
Aus
"wenn etwas wahrscheinlich ist, ist es garantiert nicht sicher", folgt aber,
dass die beiden Sicherheiten
 und
und
 ausgeschlossen
sind, so dass nur
ausgeschlossen
sind, so dass nur
 übrig bleibt.
übrig bleibt.
(Nebenbei: wenn "Wahrscheinlichkeit" das Unterrichtsthema ist, werden im Standardunterricht fast nur "echte" Wahrscheinlichkeiten [also ungleich 0 oder 1] durchgenommen, so dass die Schüler diese automatisch voraussetzen und gerade deshalb der Begriff der "echten" Wahrscheinlichkeit untergeht. Statt dessen müssten
viel mehr Schein-Wahrscheinlichkeiten, also Sicherheiten [Wahrscheinlichkeit 0 oder 1] durchgenommen werden
und damit die Einstiegsfrage bei jeder Aufgabe sein:
"Liegt hier überhaupt echte Wahrscheinlichkeit vor?".
Und wenn die Antwort "ja" ist, muss immer wieder ausdrücklich gesagt werden:
"Alle Ergebnisse sind möglich, aber keines ist sicher."
Aber Ergebnisse können
gleichwahrscheinlich sein
oder wahrscheinlicher als andere,
weshalb
man paradoxerweise eben doch Aussagen über den Zufall machen können
und Wahrscheinlichkeitsrechnung überhaupt sinnvoll ist.)
 :
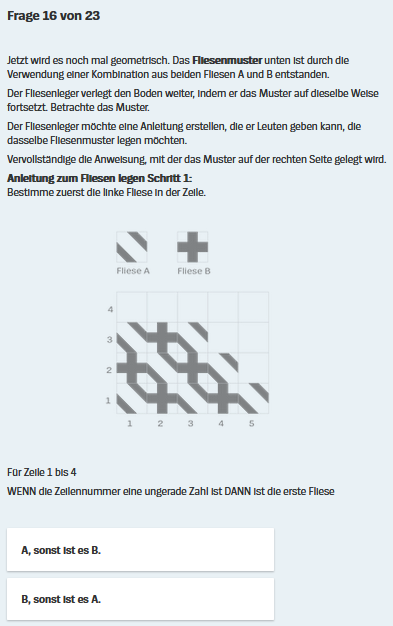
:wenn man von "gerade [Zahl]" und "ungerade [Zahl]" und simpelsten Additionen (m + n) absieht, geht es in all diesen Fragen nur um die Fortsetzungen geometrischer Muster
(vgl.
 : ein
Thema, das meiner Meinung nach im üblichen Matheunterricht meistens sträflich
vernachlässigt wird),
: ein
Thema, das meiner Meinung nach im üblichen Matheunterricht meistens sträflich
vernachlässigt wird),
In allen Fragen 16 - 20 kommt also keinerlei bemerkenswertes Rechnen vor.
Schauen wir uns aber dennoch mal an, was die Schüler denn statt Rechnen können müssen:

Kürzer:
 , woraus folgt,
dass richtig ist.
, woraus folgt,
dass richtig ist.
(Nebenbei: ich vermute, dass einige Schüler [wie auch bei den folgenden Fragen] Schwierigkeiten damit hatten, was hier mit dem Wort "sonst" gemeint ist:
anfangs wurde nach den ungeraden Zeilen [1, 3 ...] gefragt,
"sonst" bedeutet hier also, dass nun nach den geraden Zeilen [2, 4 ...] gefragt wird.)
Hier müssen die Schüler also "nur"
die ungeraden
Zeilen 1 und
3 erkennen und dass in beiden Fällen
eine ![]() die erste
Fliese ist,
die erste
Fliese ist,
die einzige
gerade Zeile 2 ("sonst") erkennen
und dass da
![]() die
erste Fliese ist,
die
erste Fliese ist,
beide Erkenntnisse für alle ungeraden / geraden Zahlen verallgemeinern.
Der Sinn dieser Einleitungsaufgabe scheint also zu sein, dass die Schüler für die folgenden Aufgaben erkennen:
in der ersten Spalte wechseln sich
die Fliesen vom Typ ![]() und Fliesen vom Typ
und Fliesen vom Typ
![]() immer ab;
immer ab;
eine erste Überprüfung ergibt, dass das für alle Spalten gilt;
das in allen Fragen 16 - 20
identisch vorkommende Flechtmuster
 ist also
ausschließlich aus den Fliesen vom Typ
ist also
ausschließlich aus den Fliesen vom Typ
![]() und
Fliesen vom Typ
und
Fliesen vom Typ
![]() zusammengesetzt und somit viel einfacher konstruiert, als man auf
den ersten Blick annehmen könnte.
zusammengesetzt und somit viel einfacher konstruiert, als man auf
den ersten Blick annehmen könnte.
(Nebenbei: solche Flecht- bzw.
Zopfmuster sind sogar schön
 , was allerdings in
der mathematischen Abstraktion
, was allerdings in
der mathematischen Abstraktion
 weitgehend abhanden
kommt. Warum also für ach so Wichtiges wie einen PISA-Test nicht [notfalls mit
Photoshop imitierte] echte Fliesen
weitgehend abhanden
kommt. Warum also für ach so Wichtiges wie einen PISA-Test nicht [notfalls mit
Photoshop imitierte] echte Fliesen
 nehmen?)
nehmen?)
Auf den Diagonalen liegen
entweder nur
Fliesen vom Typ
![]()
oder nur
Fliesen vom Typ
![]() .
.
Noch kurz zu
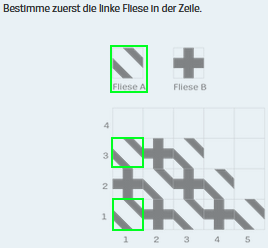 : da erscheint
sowohl in der (von unten gezählt) ersten als auch in der dritten Zeile als erste
Fliese
: da erscheint
sowohl in der (von unten gezählt) ersten als auch in der dritten Zeile als erste
Fliese ![]() , also in
beiden Zeilen (Plural) dieselbe Fliese (Singular). Das widerspricht natürlich
jeder Fliesenlege-Praxis,
, also in
beiden Zeilen (Plural) dieselbe Fliese (Singular). Das widerspricht natürlich
jeder Fliesenlege-Praxis,
bei der jede Fliese nur einmal auftaucht,
wenn auch viele Fliesen (Plural) dasselbe
Muster (Singular) haben, nämlich
![]() entweder oder
entweder oder
![]() .
.

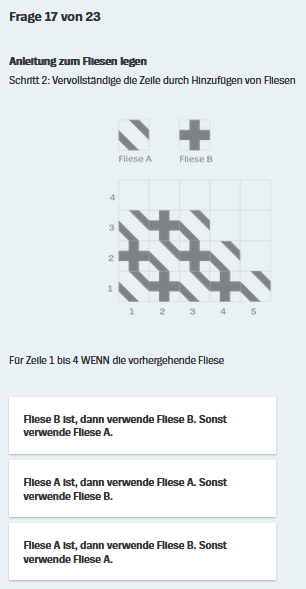
 :
hier ist
:
hier ist
nicht mehr von einer einzigen (der aktuellen) Fliese die Rede
sondern von zwei Fliesen (der aktuellen und der der vorherigen).
Hier bei Frage 17 wird die Erkenntnis aus Frage 16, dass sich
in den Spalten die Fliesen vom Typ
![]() und Fliesen vom Typ
und Fliesen vom Typ
![]() abwechseln, analog für die Zeilen hergeleitet, d.h. die richtige
Antwort ist
abwechseln, analog für die Zeilen hergeleitet, d.h. die richtige
Antwort ist 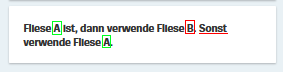 .
.
Die Fragen 16 und 17 zusammen machen also
"nur" klar, dass hinter dem unübersichtlichen Muster
 das viel
übersichtlichere Muster
das viel
übersichtlichere Muster
 steckt. Das aber ist
Voraussetzung dafür, dass man bei den Fragen 18 - 20 ((s.u.) von den
Ausschnitten
steckt. Das aber ist
Voraussetzung dafür, dass man bei den Fragen 18 - 20 ((s.u.) von den
Ausschnitten
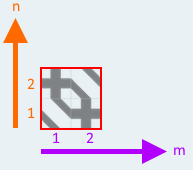 auf alle Fliesen
verallgemeinern kann. Dass für vollständige Beweise aber eigentlich begründete
Verallgemeinerungen nötig sind, werden viele Schüler gar nicht erkennen, und
dazu haben sie ja in einer stressigen Prüfungssituation vermutlich auch gar
keine Zeit. Das kann den Schülern jedoch egal sein, da die PISA-Tests im
multiple-choice-Verfahren stattfinden und somit nur zählt, ob die
Antworten richtig sind. Das entscheidet sich jedoch bei den Fragen 18 - 20 immer
schon korrekt anhand der rot umrandeten Fliesen in
auf alle Fliesen
verallgemeinern kann. Dass für vollständige Beweise aber eigentlich begründete
Verallgemeinerungen nötig sind, werden viele Schüler gar nicht erkennen, und
dazu haben sie ja in einer stressigen Prüfungssituation vermutlich auch gar
keine Zeit. Das kann den Schülern jedoch egal sein, da die PISA-Tests im
multiple-choice-Verfahren stattfinden und somit nur zählt, ob die
Antworten richtig sind. Das entscheidet sich jedoch bei den Fragen 18 - 20 immer
schon korrekt anhand der rot umrandeten Fliesen in
 .
.
(Nebenbei:
hier sei von den zwei unterschiedlichen
möglichen Orientierungen der Fliesen
vom Typ
![]() abgesehen:
sie können so
abgesehen:
sie können so ![]() oder
so
oder
so ![]() verlegt
werden [in den Fragen tritt aber nur der Fall
verlegt
werden [in den Fragen tritt aber nur der Fall
![]() auf];
auf];
man könnte zusätzlich noch feststellen: auf den Diagonalen liegen
entweder
oder
nur
Fliesen vom Typ
![]() .
.
Als nette kleine Dreingabe zwischendurch: wie musste der Fliesenleger vorgehen, als er in unseren Bädern, Klos und unserer Küche
mit den drei Fliesentypen
![]() ,
,
![]() und
und
![]()
das Muster
 legen
wollte,
legen
wollte,
und zwar, indem er die Fliesen immer
parallel zu einer Wand verlegte:
 ?
?
Und am besten lasse man Schüler das Muster mit echten Fliesen [ohne Mörtel] oder zumindest farbigen Plättchen legen.)

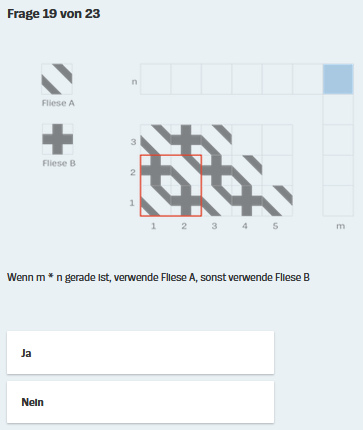
Weil ich selbst drauf reingefallen bin: :
ab hier ist
:
ab hier ist
nicht mehr von zwei Fliesen (der aktuellen und der der vorherigen) die Rede,
sondern nur noch von einer einzigen (der aktuellen).
Zuerst mal zu den rot
umrandeten vier Fliesen:
 Darin hinterlegen
wir nun
Darin hinterlegen
wir nun
oliv, wenn m + n ungerade ist,
gelb, wenn m + n gerade ist:

Also sind
Fliesen, bei denen
m + n
ungerade
ist, immer Fliesen vom Typ
![]() ,
,
Fliesen, bei denen
m + n
gerade
ist, immer Fliesen vom Typ
![]() ,
,
und deshalb ist die
Behauptung ![]() falsch
und die richtige Antwort also
falsch
und die richtige Antwort also
 .
.
Und das muss viele Schüler doch enorm irritieren:
"falsch",
"richtig",
"nein".
Hinzu kommt ein psychologischer Effekt: zumindest deutsche Schüler bekommen im Mathematikunterricht fast ausschließlich Behauptungen vorgesetzt, die richtig sind. In den meisten Fällen werden sie kritiklos geglaubt ("friss oder stirb") und sofort innermathematisch "angewandt". Und ab und zu werden sie auch bewiesen. Dahinter steckt ein Bild der Mathematik, aber auch des Mathematiklehrers, die / der immer recht hat
(was die Mathematik so penetrant besserwisserisch erscheinen lässt, und wer mag schon Besserwisser?!).
Deshalb wirkt die falsche
Behauptung ![]() so
suggestiv richtig, dass es großen Muts Und Selbstbewusstseins bedarf, um
so
suggestiv richtig, dass es großen Muts Und Selbstbewusstseins bedarf, um
 zu ihr zu sagen.
zu ihr zu sagen.

Zuerst betrachten wir wieder die rot umrandeten
Fliesen (langsam wird's langweilig):
 Darin hinterlegen
wir nun
Darin hinterlegen
wir nun
oliv, wenn m • n gerade ist,
gelb, wenn m • n ungerade ist:
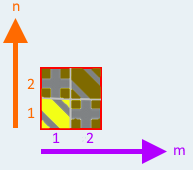
Hier sind nun sowohl Fliesen vom Typ
![]() als auch (hier
wichtiger:) Fliesen vom Typ
als auch (hier
wichtiger:) Fliesen vom Typ
![]() oliv unterlegt, also kann man
der Behauptung
oliv unterlegt, also kann man
der Behauptung ![]() nur
ein schallendes
nur
ein schallendes  entgegenschmettern.
entgegenschmettern.
In Frage 18 und 19 lautete die Antwort beide Male
img height="54" src="../bilder/pisa2_18f.png" width="281"> . Da wartet man doch
sehnlich doch darauf, dass in Frage 20 zur Abwechslung mal eine positive Antwort
 , also
, also
 folgt. Beim dritten
Versuch muss der Versuch doch endlich gelingen, denn "aller guten Dinge sind
drei".
folgt. Beim dritten
Versuch muss der Versuch doch endlich gelingen, denn "aller guten Dinge sind
drei".

Und wieder (gähn!) betrachten wir die rot
umrandeten Fliesen:

Darin hinterlegen wir nun
oliv, wenn m und n
beide gerade
oder beide ungerade sind.
gelb, wenn
eine der beiden Zahlen m und n gerade
und die andere ungerade ist:

Es folgt:
wenn
m und n
beide (un-)gerade sind, liegen Fliesen vom Typ
![]() vor
,
vor
,
sonst liegen
Fliesen vom Typ
![]() vor .
vor .
Daraus folgt aber , dass die
Behauptung ![]() (wie
oben erwartet) richtig ist, also diesmal
(wie
oben erwartet) richtig ist, also diesmal
 folgt.
folgt.
Wir haben im dritten Anlauf also endlich ein passendes mathematisches Rezept für die Fliesenverlegung gefunden.
(Das Rezept ist natürlich in
der Praxis überflüssig: ein Fliesenleger wird
![]() und
und
![]() einfach abwechselnd/span> legen.)
einfach abwechselnd/span> legen.)
 :
:
Vorweg sei festgestellt, dass das ein einschüchternd langer Aufgabentext ist
(was auch nicht dadurch besser wird, dass Teile dieses Textes auch für die Folgefragen gelten).
Ungünstig finde ich auch zweierlei:
dass der rot umrandete Teil erst nach dem grün umrandeten Teil folgt, obwohl doch der rot umrandete Teil die Voraussetzung dafür ist, dass nur den 1- und 2-Sterne-Bewertungen alle Bewertungen vorkommen, die nichts mit der Qualität der Kopfhörer zu tun haben:
 ;
;
die vielleicht für einige
Schüler schwer verständliche Kategorie
![]() : gemeint ist da
doch wohl, dass jemand eigentlich
: gemeint ist da
doch wohl, dass jemand eigentlich
![]() oder
oder
![]() vergeben wollte,
aber versehentlich
vergeben wollte,
aber versehentlich
![]() oder
oder
![]() eingegeben
(angeklickt) hat.
eingegeben
(angeklickt) hat.
Man kann bei den Aufgaben 21 - 23 natürlich auch
die Prozentangaben in der ersten Tabelle
 benutzen (z.B. 29 %),
aber weil in der zweiten Tabelle
benutzen (z.B. 29 %),
aber weil in der zweiten Tabelle
 nur absolute Werte
auftauchen (z.B. 13), ist es doch ratsam, auch in der ersten Tabelle
nur absolute Werte
auftauchen (z.B. 13), ist es doch ratsam, auch in der ersten Tabelle
 nur die Absolutwerte
(z.B. 48) zu benutzen. So gesehen sind die Prozentangaben in der ersten Tabelle
nur Blendwerk, das die Schüler hübsch vom rechten Pfad der Tugend abbringt.
nur die Absolutwerte
(z.B. 48) zu benutzen. So gesehen sind die Prozentangaben in der ersten Tabelle
nur Blendwerk, das die Schüler hübsch vom rechten Pfad der Tugend abbringt.

Um vorerst nicht mit ach so schwierigen Prozenten rechnen zu müssen, lassen wir in der ersten Tabelle alle Prozentangaben weg
(um Gottes willen nicht unnötig viel auf einmal!):

(Das aber ist [insbesondere
mit
![]() ] eine derart simple Addition, dass ich da gar nicht von "[problematischem]
Rechnen" reden möchte.)
] eine derart simple Addition, dass ich da gar nicht von "[problematischem]
Rechnen" reden möchte.)
Insgesamt haben also 163 Menschen Bewertungen abgegeben.
Da nur in den 1- und 2-Sterne-Bewertungen Begründungen vorkommen, die nichts mit der Qualität der Kopfhörer haben,
schauen wir uns nun die Tabelle für die 1- und 2-Sterne-Bewertungen an,
streichen darin alle Bewertungen, die nichts mit der Qualität der Kopfhörer zu tun haben
und addieren die Anzahlen der tatsächlich negativen Qualitätsbewertungen:
(Nebenbei: die simple Addition 7 + 4 = 11 wird man wohl kaum als
"[problematisches] Rechnen" bezeichnen wollen, und das schon gar nicht, wenn
einige Schüler dafür
![]() bemühen.)
bemühen.)
Insgesamt haben also von denjenigen Personen, die 1- oder 2-Sterne-Bewertungen abgegeben haben, 11 Personen negative Bewertungen der Kopfhörerqualität abgegeben.
Daraus folgt, dass auch von allen 163 bewertenden Personen nur 11 Personen
negative Bewertungen der Kopfhörerqualität abgegeben haben. Der relative Anteil
der negativen an allen Bewertungen war also
![]() . Um daraus eine
Dezimalzahl zu machen, benutzen wir
. Um daraus eine
Dezimalzahl zu machen, benutzen wir
![]()
(womit auch wieder kein [problematisches] Rechnen vorliegt)
und erhalten ![]() ≈0,067.
Da in
≈0,067.
Da in ![]() aber nach dem
"prozentualen Anteil" gefragt ist, müssen wir zuguterletzt 0,067doch noch kurz
in Prozente umwandeln:
aber nach dem
"prozentualen Anteil" gefragt ist, müssen wir zuguterletzt 0,067doch noch kurz
in Prozente umwandeln:
0,067 entspricht 6,7 %
Da muss es auf Schüler, deren Lösungsweg durchaus richtig war, doch allemal
irritierend wirken, dass das Ergebnis 6,7 % in der Liste
 möglicher Antworten
gar nicht vorkommt. Denkbare Reaktionen der Schüler scheinen mir zu sein:
möglicher Antworten
gar nicht vorkommt. Denkbare Reaktionen der Schüler scheinen mir zu sein:
derart in die Irre geführt, fangen sie die Aufgabe nochmals von vorne an und
kommen entweder zum selben, immer noch irritierenden Ergebnis
und verheddern sich damit vollends
(wodurch sie keine Zeit mehr für die Folgeaufgaben haben)
oder geben resigniert auf
(und raten dann hoffentlich noch in der Hoffnung, dass auch ein blindes Huhn mal ein Korn findet),
oder verschlimmbessern ihre ursprüngliche richtigen Lösungsweg und kommen dadurch
zu gar keinem (falschen) Wert aus der
Liste 
(und können dann nur noch raten)
oder zu einem falschen Wert aus dieser Liste,
verlieren mit all dem aber allemal viel Zeit;
oder sie nehmen einfach den am nächsten an 6,7
% liegenden Wert, also
(wobei sie ja nichtmal erkennen müssen, dass
das eine Rundung an der ersten Nachkommastelle ist
und auch schon 6,7 % ein an der zweiten Nachkommastelle gerundet war).
Die Irritation kann also durchaus Absicht der Aufgabenautoren gewesen sein, um nebenher auch noch das Runden abzuprüfen.
(Nebenbei: es ist natürlich nurmehr wirklichkeitsfremd, dass Andrea sich wirklich alle 163 Bewertungen angeschaut hat. Sonst hätte sie aber nicht herausfinden können, dass nur in den 1- und 2-Sterne-Bewertungen auch Bewertungen vorkommen, die nichts mit der Qualität der Kopfhörer zu tun haben. Nur soviel zum Thema "[angebliche] Anwendungsaufgaben".)

Da diese Aufgabe mit anderen Zahlen genauso funktioniert wie die vorherige
(mathematisch also nichts Neues unter der Sonne),
erledigen wir sie im Schweinsgallop:
aus der Tabelle
 und da
und da
![]() folgt, dass
41 Personen 1- und 2-Sterne-Bewertungen
abgegeben haben;
folgt, dass
41 Personen 1- und 2-Sterne-Bewertungen
abgegeben haben;
aus der Tabelle
 und da
und da
![]() folgt, dass
17 Personen bemängelt haben, dass die
Kopfhörer zu spät oder nie angekommen sind;
folgt, dass
17 Personen bemängelt haben, dass die
Kopfhörer zu spät oder nie angekommen sind;
der relative Anteil ist also
![]() ≈ 0,41 und der
prozentuale Anteil somit
≈ 0,41 und der
prozentuale Anteil somit  .
.
(Eigentlich müßig zu erwähnen, dass auch hier von "[problematischem] Rechnen" wieder keine Rede sein kann.)
Diese Aufgabe dient wie die vorherige offensichtlich allein dazu, die nächste vorzubereiten (und die Schüler mit unterschiedlichen Grundmengen zu irritieren).

Wieder im Schweinsgalopp:
aus Aufgabe 21: Anzahl aller Personen, die eine (egal, welche) Bewertung abgegeben haben: 163;
aus Aufgabe 22: Anzahl der Personen, die bemängelt haben, dass das Produkt zu spät oder nie angekommen ist: 17;
relativer Anteil:
![]() ≈ 10,4 ;
≈ 10,4 ;
richtige Antwort:
 .
.
(Es sei ausdrücklich nicht erwähnt, dass auch hier keinerlei Rechenkünste nötig sind.)
Insgesamt kann man zu den Aufgaben 21 - 23 nur sagen: was für ein gigantischer (und teilweise irreführender) Aufwand für so magere Ergebnisse!
(Obwohl ich ja durchaus weiß, dass die Schüler auch lernen müssen, knappe mathematische Informationen aus langen Texten zu destillieren.
Außerdem kann man sich ja
[wenn auch wohl nicht in einem PISA-Test]
fragen, was Andrea denn nun mit den drei doch ziemlich abgedrehten Lösungen eigentlich anfangen will, wie diese also ihre Kaufentscheidungen beeinflussen. Aber sowas wird ja im Standardunterricht kaum jemals gefragt.)
Es sollte also überdeutlich geworden sein, dass die PISA-Aufgaben den Schülern KEINERLEI nennenswertes Rechnen abverlangen.
Rechnen wir zum Rechnen auch noch dem Umgang mit "Formeln" hinzu
(also z.B. Flächen- und Körperberechnungen, binomische Formeln, Term- und Gleichungsumformungen, Funktionsberechnungen [z.B. das Berechnen von Nullstellen]).
Erstaunlicherweise kommt keine einzige dieser Formeln in den o.g. PISA-Aufgaben vor. Erstaunlich ist das aber wohl vor allem aus deutscher Sicht, macht das Rechnen mit Formeln doch ca. 90 % des üblichen Mathematikunterrichts aus.
Wundert es einen da noch, dass die deutschen Schüler so grandios in PISA gescheitert (?) sind?: das liegt
(wobei ich es hier [noch] offen lasse, ob der deutsche Mathematikunterricht nur anders, schlechter oder sogar besser ist als das, was in PISA-Tests verlangt wird).
Dass "die" deutschen Schüler so grandios gescheitert sind, kann NICHT am Rechnen gelegen haben.
Woran aber hat es dann vermutlich gelegen? Bzw. was müssen die Schüler bei den PISA-Aufgaben denn können?
Vorweg nur scheinbar selbstverständliches Allgemeines:/p>
(es sei denn, es geht um die Ersteindrücke und die später erfüllten oder enttäuschten Erwartungen),
sollten Schüler "eigentlich" immer vorweg alle Aufgaben einer Mathematik-Arbeit lesen oder zumindest grob anreißen, um
nach der Gesamtlektüre mit denjenigen Aufgaben anzufangen, die sie am besten beherrschen, und so schonmal Punkte zu sammeln und Sicherheit zu gewinnen,
die Struktur und "Dramaturgie" der Arbeit zu verstehen
(in welche Themenbereiche gliedert sich die Arbeit, worin ähneln / unterscheiden die Aufgaben sich, wie ergänzen und steigern sie sich ...?).
Leider meinen aber viele Schüler, durch eine anfängliche Gesamtlektüre unnötig Zeit zu verlieren, und stürzen sich deshalb sofort blindwütig oder in nackter Panik auf die erste, aber nicht unbedingt beste Aufgabe.
Um die Schüler zu einer anfänglichen Gesamtlektüre zu überzeugen, muss sie vor einer Klassenarbeit vielfach geübt und müssen ihre Vorteile aufgezeigt werden.
(Ich habe sogar mal [vermutlich lehrplanwidrig] Klassenarbeiten schreiben lassen, in denen
es nur um die Struktur dieser Arbeiten ging
und gesagt werden musste, was in den einzelnen Aufgaben zu tun wäre, ohne das es dann wirklich getan [z.B. gerechnet] wurde.)
(u.a. durch Vergleich mit benachbarten Aufgaben).
Auch das muss vorweg und immer wieder geübt werden, und sei's, indem man zeigt, wie Schulbuchautoren und Lehrer die Mathematik manchmal fast schon sadistisch in fast beliebige "Anwendungs"-Zusammenhänge verpacken und dort verstecken, auf dass die Schüler sie da später mühsam wieder rausklamüsern.
Schauen wir uns aber nochmals die oben vorgeführten Lösungswege an:

 :
:
 :
:
 :
:
 :
:
| PS: |
(Quelle: |