obligatorische Vorbemerkung (Blabla?)
eine mögliche Aufgabe

 

 

 

 

 

 

 

 

 

Zweifelsohne lässt sich prächtig streiten über

• ,

• PISA-Aufgaben

• und sowieso natürlich über den amokähnlichen kultusbürokratischen Aktionismus, der aus PISA folgt.

Aber die (meisten) "typischen" PISA-Aufgaben

(z.B. ; oder vgl. auch die inzwischen nach ihrem "Erfinder" so genannten "Herget-Aufgaben":  )

finde ich doch allemal besser als die Standardaufgaben im üblichen deutschen Mathematikunterricht.

Noch interessanter fände ich aber "Aufgaben", bei denen nicht mal mehr (wie auch noch bei PISA-Aufgaben) die Aufgabenstellung vorgegeben ist, sondern überhaupt erst zu entwickeln ist.

Also: wo an ist denn überhaupt die Aufgabe?

Da sind zweifelsohne mehrere Aufgaben denkbar - obwohl ich eine ganz bestimmte im Auge habe:

 

 

 

 

 

 

 

 

 

 

 

 

 

Was ist schwerer,
Kaffee oder Kondensmilch?

Anders gesagt: was mich an der ganzen Verpackung überhaupt nur interessiert, ist .

(MathematikerInneN und insbesondere PhysikerInneN wird bei der Gleichsetzung von Gramm und Millilitern natürlich schlecht, aber [und das ist im Unterricht zu bedenken!] im Alltag ist das der Einfachheit halber gang und gäbe. Wie sollte denn auch die Alternative aussehen?: 340 g entsprechen 317 ml???)

Die Antwort ist "also" 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Kondensmilch ist schwerer als Kaffee

(... wobei ich mal ungeprüft voraussetze, dass Kaffee etwa genauso schwer ist wie das Wasser, aus dem er hergestellt wird: das bisschen hinzugefügtes Kaffeemehl [oder genauer: der Extrakt nach Filterung] macht sicherlich [?] "den Kohl auch nicht fett".)

Das Problem dabei ist allerdings das "also" in "die Antwort ist »also«", denn dieses "also" suggeriert doch, dass die Antwort ganz einfach und im Grunde selbstverständlich ist

(und wer da nicht folgen kann oder will, ist halt - wie üblich - dumm und hat sich von jeder weiteren Diskussion selbst ausgeschlossen).

---

Wieso nenne ich die Frage "Was ist schwerer, Kondensmilch oder Kaffee?" eine typische PISA-Aufgabe?

1. , weil da

(anders als sogar in )

keine Antwort suggeriert wird, denn es wäre doch beides denkbar:

• sowohl, dass Kondensmilch schwerer als Kaffee ist,
• als auch das Umgekehrte.

(Ich werde noch darauf zurück kommen, ob wirklich beides denkbar bzw. naheliegend ist.)

2. , weil mehr noch bei der Gesamtpackungsseite als bei dem Ausschnitt 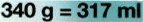nicht auf Anhieb klar ist, worin der entscheidende Tipp zur Beantwortung der Frage liegt.

3. , weil keinerlei Lösungs- oder gar Rechenanweisung mit gegeben wird.

4. , weil man

(ganz im Gegensatz zum üblichen deutschen Matheunterricht)

überhaupt nicht rechnen muss

(wobei es natürlich fraglich ist, ob hier überhaupt eine Mathematik- oder nicht doch eher eine Physikaufgabe vorliegt).

5. , weil man zur Lösung der Aufgabe "nur" einige "selbstverständliche" (?, s.u.) Grundkenntnisse kombinieren (statt eben rechnen) muss, nämlich

• 317 ml Kondensmilch wiegen 340 g

• 317 ml Kaffee (genauer genommen: Wasser) wiegen aber exakt 317 g

(genau so - wenn auch im Grunde um einige Ecken - ist das Gramm ja definiert: als das Gewicht von einem Milliliter Wasser;
und wieder: dem Alltagsgebrauch entsprechend wird hier von "Gewicht" und nicht von "Masse" gesprochen: der Begriff "Masse" kommt im alltäglichen Sprachgebrauch gar nicht [zumindest nicht in der physikalischen Bedeutung] vor, und den Unterschied zwischen Masse und Gewicht versteht eh kein Laie).

• also wiegt Kondensmilch mehr als Kaffee.

Nun könnte man zwar sagen, dass die zur Lösung der Aufgabe notwendigen Kenntnisse

(und "kombinatorischen" Fähigkeiten!)

"eigentlich" zur Grundausstattung, wenn nicht gar Allgemeinbildung aller SchülerInnen gehören müssten *

(* Optativ oder doch eher Irrealis²⁷?)

... und der Untergang des Abendlandes längst im Gange ist, weil die durchschnittlichen SchülerInnen

(so unterstelle ich mal ohne alle Vorwürfe)

diese Kenntnisse vermutlich nicht haben und schon bei der Volumeneinheit "ml" scheitern.

---

Die zentrale Ursache für solche  Probleme liegt meiner Meinung nach darin, dass alltägliche Erfahrungen für SchülerInnen ganz grundsätzlich keine Beziehung zu schulischen (insbesondere mathematischen) "Gegenständen haben; vgl. .

(... und dass viele SchülerInnen sich über überhaupt nichts mehr wundern?).

Also wird´s Zeit, den "mathematischen" Kaffee mit dem "realen" zu verbinden.

Wir fangen also eine Unterrichtseinheit überhaupt nicht mit der Frage "Was ist schwerer, Kaffee oder Kondensmilch?"

(mit überhaupt keiner [offensichtlichen] Frage),

ja nichtmal mit an, sondern mit der simplen Aufgabe:

Beobachte, was passiert, wenn Du Kondensmilch in Kaffee schüttest.

Da gibt es eine ganze Reihe ebenso schöner wie physikalisch bedeutsamer Effekte

(und ich glaube ja sowieso, dass man die halbe Naturwissenschaft an Alltagseffekten aufhängen kann - und sollte: ),

von denen uns aber im Folgenden nur einer interessiert:

die Kondensmilch sinkt
striktemang nach unten!

Warum?

 

 

 

 

 

 

 

 

 

 

 

 

Hier kommt erstmals der Grund ins Spiel, weshalb mir die hier behandelte Aufgabe überhaupt bei der zufälligen Betrachtung von aufgefallen ist.

Mein erster Gedanke bei war nämlich schon relativ abstrakt

(und dazu musste ich auch nicht mehr großartig "kombinieren"):

"das [egal welches] Zeug ist

• wegen ähnlicher Größenordnung ähnlich schwer wie Wasser

[auf Kondensmilch bezogen kein Wunder, da sie doch vermutlich großteils aus Wasser besteht],

• aber doch ein wenig schwerer."

Ich hatte zwar nie vorher darüber nachgedacht, warum Kondensmilch nach unten sinkt, sondern mir war nur der Effekt dieses Absenkens bekannt bis geradezu (allzu) selbstverständlich.

(Nochmals: manchmal frage ich mich in der Tat, ob SchülerInnen solche alltäglichen Effekte überhaupt noch mitbekommen.)

Die Betrachtung von brachte nun aber bei mir ein (erstes) "Vorurteil"

1. ebenso überhaupt erst an den Tag wie auch

2. im selben Augenblick zum Einbruch,

und gerade dieser Doppeleffekt versetzte mich so in Staunen.

Das Vorurteil bestand darin, das Absinken der Kondensmilch (allein) dadurch zu erklären, dass

• der Kaffee üblicherweise heiß aus der Kaffeemaschine und

• die Kondensmilch üblicherweise kalt aus dem Kühlschrank kommt

• und

(wieder so ein Stück "Allgemeinbildung")

Warmes (der Kaffee) nach oben steigt bzw. Kaltes (die Kondensmilch) nach unten sinkt

(wozu mir auf Anhieb nur die - richtige? - Erklärung einfällt, dass Warmes sich

[wegen zunehmender Molekülbewegung?]

ausdehnt, also pro Volumeneinheit leichter wird).

Dieses Vorurteil - so scheint mir aber im Nachhinein - war nur zur Hälfte falsch, aber eben auch zur anderen Hälfte richtig:

dass die Kondensmilch im Kaffee nach unten sinkt, kann ja zwei Ursachen haben:

1. eben laut "Vorurteil", dass die Kondensmilch kälter ist,

2. , wie wir inzwischen wissen, weil sie auch schwerer ist.

In einem Atemzug wurde bei mir allerdings noch ein anderes, zweites

(dem ersten geradezu widersprechendes!)

Vorteil gekippt: Zwar hatte ich mir nie vorher einen Gedanken darüber gemacht, aber ich hätte doch immer geschlossen:

1. ist Kondensmilch sehr fetthaltig

(allemal fetthaltiger als [Kaffee-]Wasser)

und

2. ist es inzwischen sogar sprichwörtlich (im übertragenen Sinne) geworden: "Fett schwimmt oben."

Ein besonders netter Effekt ist nebenbei das Zeitlupen-Schwappen der untersten Milchschicht in Latte macchiato.