das Staunen in der Mathematik
oder
die Spannkraft eines Funktionsgraphen

Anlass für diesen Essay war die Aufgabe

»«

aus einem Schulbuch.

Die durch die Aufgabe vorgegebenen, allerdings allesamt hübsch versteckten

(damit die Schüler sie garantiert nicht finden!?)

mathematischen Informationen sind äußerst knapp:

  1. 1.: eine Funktion dritten Grades, also mit einer Funktionsgleichung der Form y = ax3 + bx2 + cx + d ,
  1.  a.
2.: der Ursprung U (0 | 0) liegt auf dem Funktionsgraphen bzw. der Graph geht durch U ⇒ f   (  0 ) = 0 ,
3.: P (-3 | 0) liegt auf dem Funktionsgraphen bzw. der Graph geht durch P                       ⇒ f   ( -3 ) = 0 ,
b.

4.: die Funktion hat in U (0  | 0) die Steigung 0                                                                      ⇒ f ' (  0 ) = 0 ,
5.: die Funktion hat in P (-3 | 0) die Steigung 6                                                                      ⇒ f ' ( -3 ) = 6 :

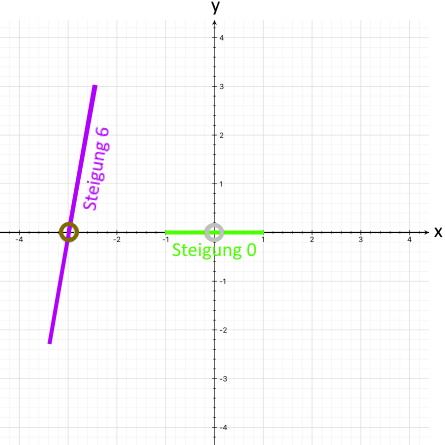
Und aus diesen lächerlichen fünf Informationshäppchen sollen sich allen Ernstes die Funktionsgleichung und damit auch der gesamte Funktionsgraph ergeben???

Nun lässt sich mit den fünf Informationshäppchen alles stumpf runterrechnen

(vgl.  ),

und dann bekommt man

(um - über die Aufgabenstellung hinausgehend - den Funktionsgraphen zeichnen zu können und damit überhaupt erst eine anschauliche Vorstellung von der Funktion zu bekommen)

mittels klassischer „Kurvendiskussion“

(vgl. )

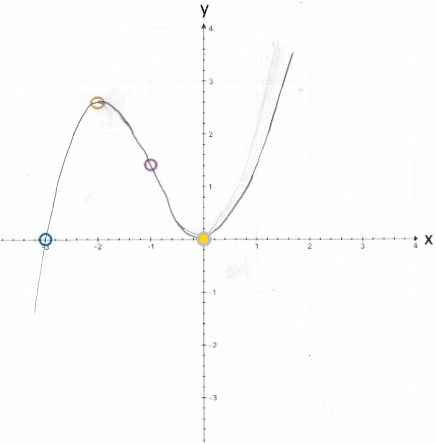
womit sich endlich halbwegs genau der Funktionsgraph zeichnen lässt:

Oder um Einiges genauer:

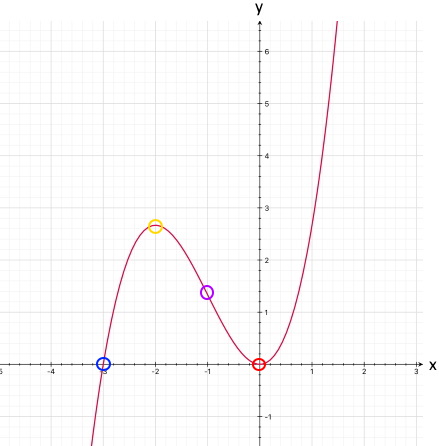
An all dem ist

(zumindest auf den ersten Blick)

gar nichts staunenswert, sondern das ist alles schnödes

(und damit abstoßend langweiliges und sowieso völlig abstraktes)

Rechnen nach Notwendigkeit.

A propos „nach Notwendigkeit“:

so langweilig die Aufgabe an sich ja ist, wenn man sie nur schnöde runterrechnet, so finde ich es doch höchst erstaunlich, dass

(also insgesamt nur die vier Informationshäppchen 2., 3., 4. und 5.)

reichen,

(unter der zusätzlichen Voraussetzung 1., dass eine Funktion dritten Grades vorliegt)

"Wer das Geheimnisvolle nicht kennt
und sich nicht mehr wundern,
nicht mehr staunen kann,
der ist sozusagen tot
und sein Auge erloschen."
(immer ein probates Killerargument: Albert Einstein)

Ich höre schon, wie einige notorische Schlaumeier mich belehren:

(also solchen mit den Funktionsgleichungen y = ax3 + bx2 + cx + d ),

diejenige (einzige?!) Funktion gesucht wird, die die in der Aufgabe genannten vier Bedingungen 2., 3., 4. und 5. erfüllt,

Anders gesagt:

passt doch wie Po auf Klo - und ist nicht im mindesten staunenswert!

"Staunen ist eine Emotion beim Erleben von Unerwartetem."
(Quelle: )

Es gibt sicherlich auch ein Staunen über Negatives: "Ich war erstaunt [und entsetzt], als ich erfuhr, dass der bislang so nett wirkende Erwin regelmäßig seine Frau schlägt."

In der Regel staunt man jedoch wohl eher über Positives, also z.B. über .

Aber ist solch ein Sonnenuntergang wirklich - wie es in der Wikipedia-Definition heißt - unerwartet? Das könnte man doch eigentlich nur bei jemandem sagen, der

Bedeutet "unerwartet" vielleicht eher, dass jemand für etwas, über das er staunt, keine Erklärung hat? Und wenn er sie hätte (oder nachholen würde), würde er dann nicht mehr staunen

(würde alles Staunen dann schlagartig verpuffen - und emotionslosem Verständnis Platz machen)?

Kann also jemand nicht mehr über einen Sonnengang staunen, der eine Erklärung

(oder wohl eher mehrere Erklärungen)

für dieses Phänomen hat?

Über :

"Als Isaac Newton Sonnenlicht in seine Spektralfarben zerlegte, warf man ihm vor, er habe den Zauber des Regenbogens zerstört. Doch das Wunderbare ist nicht weniger wunderbar, wenn wir es erklären können, sagt Richard Dawkins und entwirft ein leidenschaftliches Plädoyer für die Poesie in der Wissenschaft."
(Quelle: )

Und für James Trefil war klar:

"Ein Forscher, der über den [Strand] spaziert [und einen Sonnenuntergang beobachtet], sieht dort dieselben Dinge wie jedermann sonst. Die Tatsache, dass er über einige dieser Dinge besser Bescheid weiß, schmälert weder seine Empfänglichkeit für ihre Schönheit noch den Grad seiner Freude daran."

Das mag auch daran liegen, dass der Forscher nur über „einige“ den Sonnenuntergang betreffende Dinge besser Bescheid weiß,

(wie der naturwissenschaftlich minderbemittelte Laie)

dieses Rot so anrührend schön findet

(es mag dafür evolutionäre Gründe geben, aber selbst wenn unser Forscher sie kennen würde, würden sie doch sehr abstrakt bleiben und deshalb sein Gefallen am Sonnenuntergang keineswegs abwürgen können).

Mir scheint allerdings, dass Trefil zu allgemein von „einem“ Forscher spricht, was paradoxerweise doch eher „alle“ Forscher bedeutet

(oder zumindest alle, die ein wenig Ahnung von Optik und Meteorologie haben):

es gibt vielleicht doch auch Forscher, die überhaupt nicht mehr über ihr Fachgebiet staunen können.

(Wie sehr habe ich mich im Studium nach Professoren gesehnt, die auch mal sagten, warum sie ihr einmaliges Leben der Wissenschaft widmeten - und dass sie noch immer über ihr Fachgebiet staunen konnten!)

Da frage ich mich dann doch, warum solche Forscher ihr Fachgebiet überhaupt gewählt haben: hatten sie von Anfang an nicht dieses Staunen, oder haben sie es im Laufe der Zeit verloren?

Oder gehört es in der Wissenschaft (leider!) zum guten Ton, immer hübsch brav sachlich zu bleiben?:

"Lass dir niemals anmerken, dass du Spaß an der Wissenschaft hast!"

Und überhaupt sind Emotionen ja angeblich unwissenschaftlich. Im Gegenteil: sie befeuern ja überhaupt erst Wissenschaft: "ich will was [genau] wissen"!

Mir scheint aber, dass die wahrhaft großen Forscher immer schon zum Staunen fähig waren und sie es sich bewahrt haben, ja, dass sie überhaupt nur deswegen zu großen Forschern werden konnten.

Und dann gibt es noch Forscher, die durchaus Emotionen haben (staunen können), denen das (die Nähe zu den Laien) aber peinlich ist und die ihre Emotionen deshalb verleugnen - womit sie nur sich selbst weh tun.

Diejenigen Forscher (und Lehrer!) aber, die mit ihren Fächern keine Emotionen verbinden oder diese Emotionen (das Staunen) leugnen, treiben die Leute (Schüler) geradezu "aus der Kirche [der Wissenschaft] raus":

Dann konvertieren die Halbakademiker massenhaft zur Esoterik, weil diese ihnen immerhin „Sinn“ bietet.

Die Laien haben dann verständlicherweise keine Lust, sich die Welt zugunsten von entzaubern zu lassen:

"Grau, teurer Freund, ist alle Theorie
und grün des Lebens goldner Baum."
(das nächste immer probate Killerargument: Johann Wolfgang Goethe, "Faust";
Nerds würden da natürlich wieder einwenden: ein goldner Baum kann nicht gleichzeitig grün sein)

Wundert es einen da noch, dass (angeblich?) zu wenige Abiturienten (und teilweise die falschen, nämlich Nerds) MINT-Fächer studieren wollen? Und könnte der ganze MINT-Hype  kontraproduktiv sein, wenn in die MINT-Fächer nicht das Staunen (wieder) Einzug hält?

Einen anderen Aspekt des Staunens zeigt ein späterer Auszug aus dem oben bereits anzitierten Wikipedia-Artikel:

"Aristoteles sieht im Staunen [...] den Beginn des Philosophierens, das einen starken Akzent auf die Verwunderung legt. Die Philosophie würdigt Dinge kritischer Betrachtung, die zunächst als selbstverständlich erscheinen [die Philosophie verzaubert die Welt also sogar wieder]. Selbstverständlichkeiten werden bezeichnet als »bloße Meinung« [...]. Bei genauem Hinterfragen von Selbstverständlichkeiten zeigen sich erstaunliche, bisher unberücksichtigte und neue Wahrheiten [...]."

Lassen wir dabei mal die Philosophie weg, die viele MINT-Fuzzis vermutlich (und völlig zu Unrecht) für reines Blabla halten

(und die sie durch Wissenschaft ersetzen, ja, oftmals geradezu rabiat ausmerzen wollen, weil sie keine Unsicherheiten und Vieldeutigkeiten ertragen: Wissenschaft als [durchaus verständliche] Flucht vor den Unwägbarkeiten des Lebens).

Interessant ist aber allemal der Rückwärtssalto

"Bei genauem Hinterfragen von Selbstverständlichkeiten zeigen sich erstaunliche [!], bisher unberücksichtigte und neue Wahrheiten [...]":

wenn man die Selbstverständlichkeiten (bloßen Meinungen) hinterfragt, zeigt sich also etwas neues Erstaunliches. Und mit jedem Enträtselten ergeben sich gleich drei  neue Rätsel.

Zuguterletzt staunt man manchmal, weil etwas "zu schön [ist], um wahr zu sein"

(z.B., wenn in der Mathematik nach unübersichtlich langer und komplizierter Rechnung plötzlich alles in einer ganz einfachen Lösung zusammenrauscht):

da weiß man oftmals kognitiv durchaus schon vorher, was "wahr" ist, und ist dennoch überrascht darüber, dass es bzw. wenn es dann tatsächlich eintritt. In der Mathematik ist das beispielsweise dann der Fall, wenn man etwas vermutet und eigentlich schon für (eine mathematische Unmöglichkeit:) "so gut wie sicher" gehalten hat - und es am Ende einer langen Beweiskette urplötzlich bewiesen dasteht: Das haben viele Mathematiker dann mangels anderer Erklärungen nur als völlig unwissenschaftliche "Offenbarung", "Gottesgabe" oder "Musenkuss" wahrnehmen können

(und manchmal hat dann sogar ein Mathematiker [gar nicht so] paradoxerweise geweint vor Glück: vgl. .

nebenbei: Descartes künstliche Trennung zwischen Gefühl einerseits und [wissenschaftlichem] Verstand andererseits

[zwischen denen man sich dann entscheiden muss?]

möchte ich eigentlich gar nicht mehr mitmachen).

Aber wieder zu meinem Staunen:

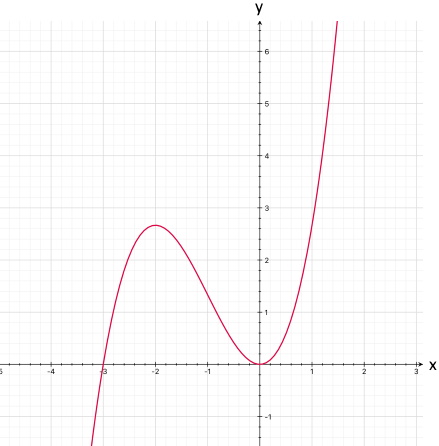
  1. kann man "trotzdem" darüber staunen, dass

möglich machen.

Schauen wir uns mal die zur Berechnung der Unbekannten a , b , c und d nötigen Rechnungen an

(vgl. ):

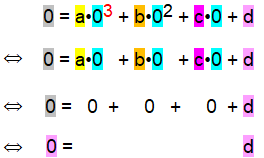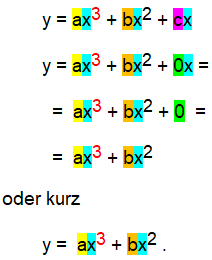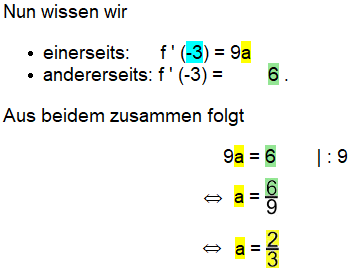Diese Rechnungen, die Schülern schwer fallen mögen, sind für gestandene Mathematiker doch höchstens eine kleine rechnerische Fingerübung: man muss nur brav die simpelsten Rechengesetze abspulen. Aber dabei ist man doch nur Sklave der notwendigen Rechnungen, und dementsprechend werden Mathematiker solche Rechnungen als sterbenslangweilig empfinden.

Und doch:

(oder wohl besser 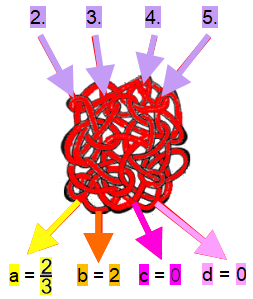; vgl. unten PS)

Es ist, als wenn

Schon hier beim ersten Staunen könnte man den Eindruck haben, dass "die" Mathematik oder hier die zum Ziel führenden Rechnungen von selbst funktionieren

(vom Menschen nur geschickt, aber ansonsten sklavisch nachvollzogen werden müssen)

und schlauer als "der" Mensch sind, dass also die Mathematik fast göttlich ist:

.

Oder um den lieben Gott

(sei's aus Pietät, sei's aus Atheismus)

aus dem Spiel zu lassen: dass die Mathematik eine ziemlich schlaue Person ist.

  1. mein zweites Staunen:

wie wir oben gesehen haben, führen die  vier Bedingungen 2., 3., 4. und 5. auf direktem rechnerischem Weg zu der Funktionsgleichung y = x3 + 2x2 und dann zu dem Funktionsgraphen

 

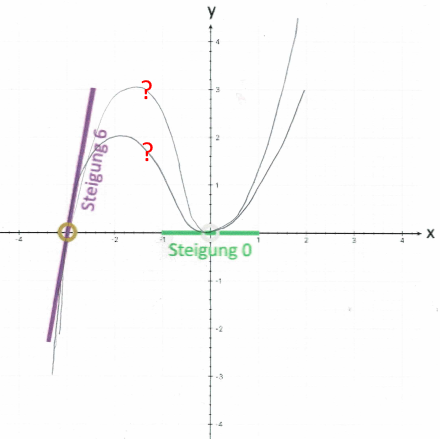
  hingegen hat‘s nicht so leicht, sondern muss mühsam mehrere halbwegs mögliche Funktionsgraphen durch die Vorgaben durchfriemeln

,

Aber weiß ohne weitere Informationen nicht, welcher der Funktionsgraphen halbwegs richtig ist. Das liegt vor allem daran, dass nicht weiß, wie hoch der Funktionsgraph im zweiten Quadranten 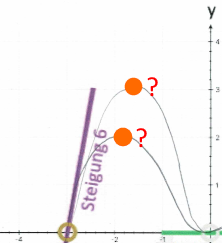liegt. Da dort irgendwo (?) das Maximum liegt, empfiehlt es sich, dieses noch zusätzlich zu berechnen

(und vielleicht auch noch - wenn man schon am Rechnen ist -  den Wendepunkt; als Minimum erhalten wir sowieso nur, was wir schon wissen, nämlich den Ursprung).

Mit diesem Zusatzwissen erhält nun folgende Punkte und Strecken

,

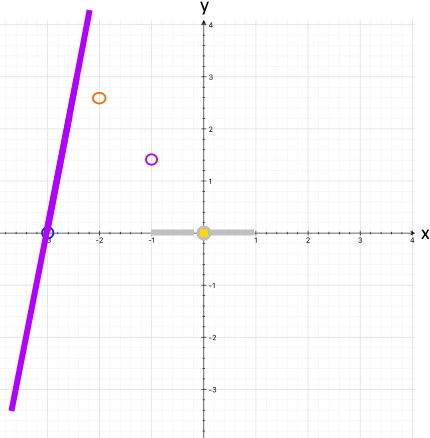und durch diese Punkte und entlang dieser Strecken schafft sogar dann endlich einen halbwegs richtigen Funktionsgraphen

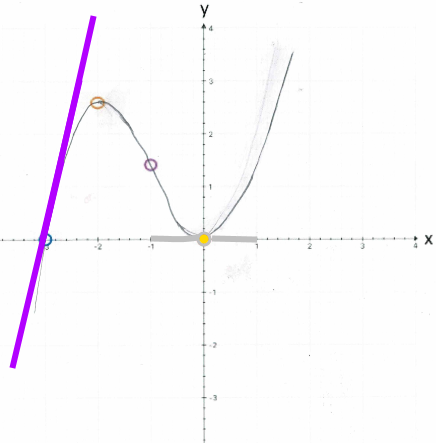
Es ist doch ungerecht : wieso

Natürlich beruht diese Einschätzung auf einem Irrtum: wie denn ist der bildschöne Funktionsgraph

entstanden?: der entscheidende (einzige?) Vorteil von Computern ist ihre Schnelligkeit:

(Nullstellen, Extrema, Wendepunkte),

(ohne überhaupt etwas von Nullstellen, Extrema und Wendepunkten zu wissen)

(und die sehr nah nebeneinander liegenden Punkte fürs menschliche Auge unmerklich durch gerade Strecken verbinden:  ).

Der vom Computer gezeichnete Funktionsgraph ist also genau genommen

(und - typisch Mathematiker! - ein bisschen spitzfindig bemerkt)

auch nur

(ein Widerspruch in sich, denn "knapp vorbei ist auch daneben":)

(also bittschön kein falscher Respekt vor Computern!).

Das liegt daran, dass Computer auch nicht unendlich viele Punkte berechnen können und somit der Funktionsgraph bei geeigneter Vergrößerung immer ein wenig "zackig" bleibt.

Damit sind wir bei einem uralten philosophischen (!; s.o.) Problem: wo ist er denn nun, der "eigentliche", der perfekte Funktionsgraph, wenn nichtmal ein Computer (geschweige denn ) ihn zeichnen kann???

Auf diese Frage gibt es, so scheint mir, zwei mögliche Antworten:

    1. es gibt den perfekten Funktionsgraphen gar nicht, sondern es bleibt uns nichts anderes, als mit (mehr oder minder guten) Annäherungen an etwas "Unsichtbares" vorlieb zu nehmen:

(Aber wie wollen wir dann beurteilen, ob eine Annäherung mehr oder weniger gut ist?)

    1.  


Platon
(* 428/427 + 348/347 v. Chr.)

hätte hingegen gesagt, dass es den Funktionsgraph sehr wohl gibt, nämlich als "Idee" im Kopf von (und nur da!).

Und da ich Platoniker von altem Schrot und Korn bin

(vgl. ),

stelle ich mir in meiner unbeschränkten imaginären Machtvollkommenheit

(denn schließlich kann und darf ich mir frisch-fromm-fröhlich-frei vorstellen, was ich lustig bin!)

einfach (!) den perfekten Funktionsgraphen zur (sowieso schon perfekten) Funktionsgleichung y = x3 + 2x2 vor:


(jetzt endlich ohne alle [wenn auch vielleicht nicht sichtbaren] Ungenauigkeiten und Zacken,
also perfekt geschwungen)

Und wo ich schon so frohgemut am Imaginieren bin, schaffe ich natürlich auch problemlos den Spagat

(da ich doch materielle Modelle liebe)

ein "Kurvenlineal" vorzustellen,

(und schon gar nicht aus mehreren Materialien, also materiellen Unreinheiten;

nebenbei: Atome und Moleküle hängen ja auch "irgendwie" [durch Elektronenbindung?] zusammen, denn sonst würde ja alle Materie in Atome und Moleküle zerbröseln),

Und jetzt bin ich plötzlich sehr großzügig: ich nehme auch gerne mit einem echten Kurvenlineal "aus Fleisch und Blut" vorlieb, weil ich seine feinen materiellen Unregelmäßigkeiten eh nicht erkennen kann.

Mit solch einem Kurvenlineal

(jetzt einem biegsamen Kunststoffstreifen mit blauer Kante )

möchte ich nun erforschen, wie der Funktionsgraph es "so mir nichts, dir nichts" schafft, die  vier Bedingungen 2., 3., 4. und 5. , also

,

zu erfüllen.

Um das herauszufinden, biege ich den Kunststoffstreifen mit möglichst geringer Kraft so, dass er

anliegt.

Was ich herausfinden möchte: wie biegt sich so ein Kunststoffstreifen, der das Glück hat, nichts von Mathematik hat und also auch Funktionen dritten Grades zu wissen?

(Die Festlegung der Aufgabenstellung auf solche Funktionen dritten Grades scheint mir ja doch willkürlich: vielleicht gibt es ja eine [was immer das sei:] bessere Lösung des Problems.)

Oder wählt der Kunststoffstreifen (annähernd) von selbst die Form des Funktionsgraphen einer Funktion dritten Grades?

 


Ich hab's ja bekanntlich mit Schlangen als Metaphern für mathematische Zusammenhänge

(vgl. ).
Weil ein Kunststoffstreifen nicht nur zu blöd für Mathematik, sondern auch für ein willentliches Sich-Biegen ist, stelle ich mir nun Folgendes vor: eine Schlange
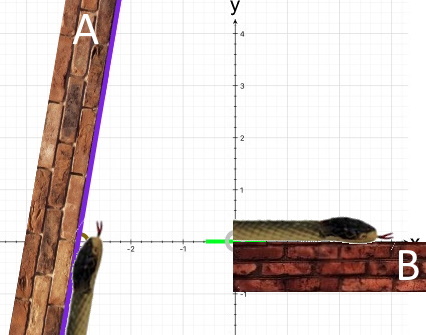  • kriecht von links unten bis zum Punkt P an der Mauer A entlang
  • und möchte dann ab dem Ursprung an der Mauer B nach rechts weiterkriechen:



Dabei ist mir durchaus bewusst, dass Schlangen sich eigentlich gar nicht direkt geradeaus bewegen können, sondern eine Vorwärtsbewegung nur durch permanentes Schlängeln erreichen können und zwar
  • entweder so (Kopf in Bewegungsrichtung)
  • oder so (Kopf senkrecht zur Bewegungsrichtung).
Aber unsere Schlange ist eben was Besonderes, nämlich so verängstigt, dass sie immer an einer beschützenden Wand entlang will - und das auch irgendwie schafft.

Weil unsere Schlange immer Mauerkontakt sucht, möchte sie auch möglichst schnell über die Lücke zwischen den beiden Mauern hinweg kommen. Der kürzeste und damit schnellste Weg zwischen beiden Bauern ist aber "eigentlich" dieser: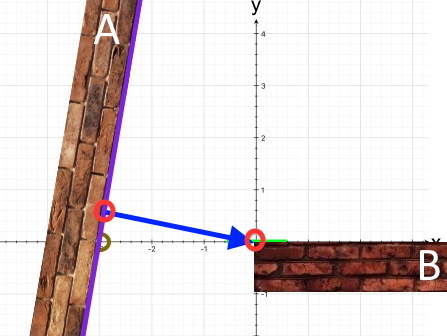



"eigentlich", weil eine Schlange keine Knicke 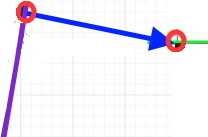"gehen" kann und sich nicht enger als auf ihrem "Wendekreis" biegen kann.

Aber warum eigentlich nicht? Schauen wir uns dazu das Skelett einer Schlange an

und daran einen vergrößerten Kurvenabschnitt:


In einer Kurve werden also
  • die äußeren Rippen auseinandergezogen
  • und die inneren Rippen zusammengequetscht:

Wenn die Kurve jetzt noch enger wird, berühren sich irgendwann die inneren Rippen:

Damit ergibt sich der kleinstmögliche „Wendekreis“ der Schlange.

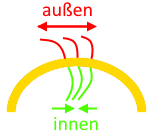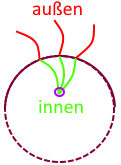Um aber eine Schlange zu begreifen, be-greift man sie am besten. Nur woher ein Schlange nehmen? Immerhin gibt es aber solch eine 1,3 m lange, erstaunlich echt wirkende und nur schlappe 13  € teure Gummischlange zu kaufen:


(Kleiner Nachteil: bei dieser Schlange kann man die Rippen nicht sehen.)

Und glücklicherweise gibt es solche Spielzeuge:


Solch eine Spielzeugschlange besitzt zwar keine Rippen, aber sie ist aus Holzscheiben aufgebaut, die durch einen biegsamen Stoffstreifen verbunden sind, und diese Kombination ist eine schöne Illustration genau jenes Aspekts einer echten Schlange, der uns hier interessiert, nämlich was passiert, wenn eine Schlange sich biegt.

Schauen wir uns dazu das vergrößerte Mittelteil der Holzschlange mal genauer an:


  • Auf der rechten, geraden Seite sind die Lücken zwischen den Holzscheiben oben und unten gleich breit.
  • Auf der linken, gebogenen Seite sind die Lücken
    • oben (außen) sehr breit,
    • unten (innen) hingegen dreieckig, so dass die Holzscheiben sich unten sogar berühren.
Und wenn man auch keine Spielzeugschlange zur Hand (!) hat, nehme man halt eine Metallfeder:


oder


Weil unsere Schlange also keine Knicke „gehen“ kann, ist sie gezwungen, einen kleinen Umweg zu "gehen":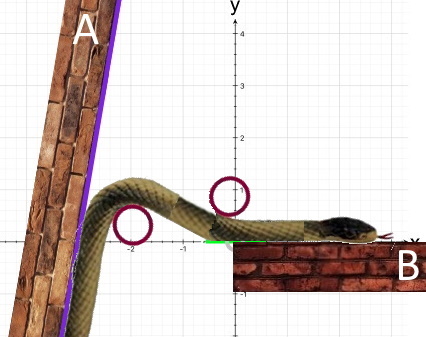



Hält sich unser Kunststoffstreifen nun aber auch an diesen (Um-)Weg?

Damit wieder zu

.

und jetzt der Frage, wie sich der Kunststoffsteifen durch diese Vorgaben windet - nämlich so:

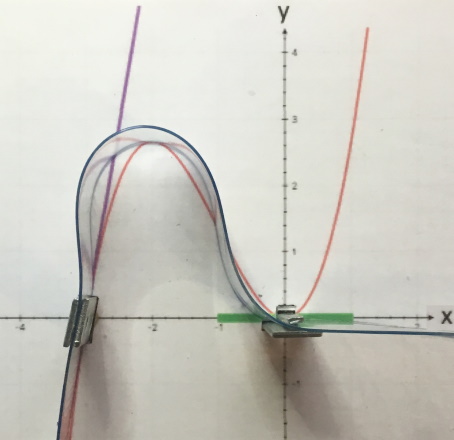
Der Kunststoffstreifen wählt also nicht

(wie erwartet oder besser erhofft)

denselben Weg wie der „richtige“ Funktionsgraph. Und wirklich schlimm: der gebogene Kunststoffstreifen stellt nichtmal eine Funktion dar, da er „rückläufig“ ist und deshalb dem x-Wert 3 mehr als ein y-Wert (nämlich z.B. 1 und 2,2)  zugeordnet wird:

Der Kunststoffstreifen ist also leider nicht so schlau wie der rote Funktionsgraph.

Nun kann man sich aber fragen, wieso hier das Kunststoffstreifen-Experiment schiefgegangen ist. Man könnte vermuten, dass der Streifen nicht biegsam genug ist und deshalb z.B. im Maximum nicht eng genug werden kann:

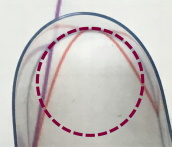
Aber mangelnde Biegsamkeit ist wohl nicht der Grund für das „Fehlverhalten“ des Kunststoffstreifens, denn ein viel dünnerer und damit biegsamerer Kunststoffstreifen zeigt dasselbe „Fehlverhalten“.

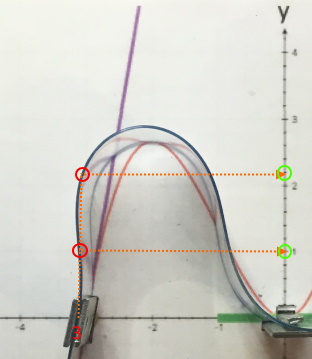
Dann wollen wir doch mal sehen, ob der Kunststoffstreifen wenigstens genauso schlau ist wie wir, die wir mit dem zusätzlichen Maximum und
Wendepunkt einen halbwegs schönen Funktionsgraphen zustande bekommen haben:

Mit dem Kunststoffstreifen ergibt sich erst Folgendes:

 Der Kunststoffstreifen nähert also den Funktionsgraphen

Wir müssen also noch zwei Punkte links unten und rechts oben hinzufügen.

Der Kunststoffstreifen braucht also zwei Punkte mehr als wir und ist - so gesehen - dümmer als wir ; dafür schafft er aber einen schöneren Graphen als wir:

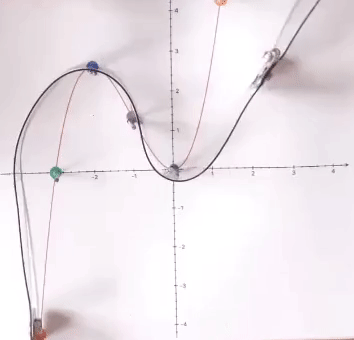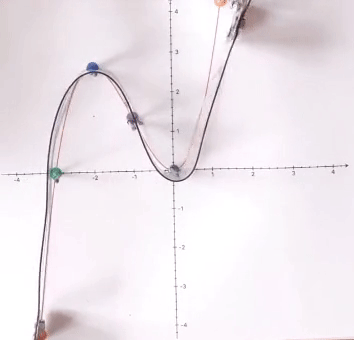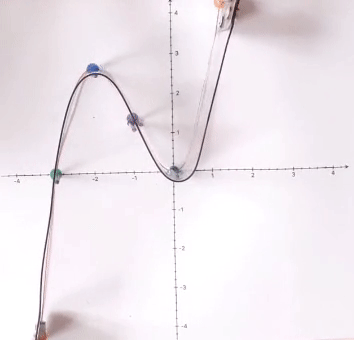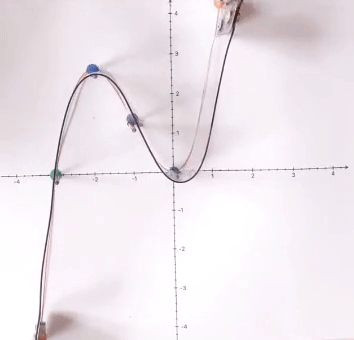
(Nebenbei ist auch die Überlegung sehr lehrreich, wo die Nägel eingeschlagen werden müssen, nämlich

: damit nähert der Kunststoffstreifen den Funktionsgraphen in dessen gesamten Verlauf erstaunlich gut an

(rechts sogar so gut, dass der Funktionsgraph unter dem Kunststoffstreifen überhaupt nicht mehr sichtbar ist).

... womit sich die Frage stellt, wie der Kunststoffstreifen es geschafft hat, den Funktionsgraphen so schön zu imitieren.

Warum verhält er sich nicht wie ein gespannter Papierstreifen, nämlich so?:

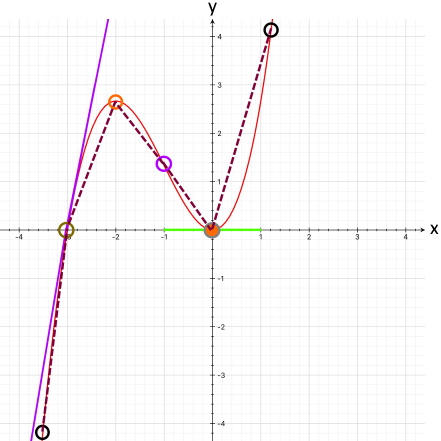
Wieso also sucht sich der Kunststoffstreifen nicht (wie der Papierstreifen) die kürzesten Punktverbindungen (Strecken - - - ), sondern geht er Umwege

(und schmiegt sich dadurch an den Funktionsgraphen an)?

Natürlich könnte man den Kunststoffstreifen auch so stramm ziehen, dass er wie der Papierstreifen einem Streckenzug folgt

(„und bist du nicht willig, so brauch ich Gewalt“),

aber

    1. würde der Kunststoffstreifen dieser Aktion erhebliche „Spannkraft“ (s.u.) entgegensetzen

(wenn man den Kunststoffstreifen immer weiter biegt, muss man eine immer größere Kraft aufwenden, weil der Kunststoffstreifen unserer Kraft immer exakt dieselbe Gegenkraft [Spannkraft] entgegen: er wehrt sich immer rabiater gegen das Biegen),

    1. bestünde Gefahr, dass der  Kunststoffstreifen überspannt, also irreparablen Schaden nehmen würde:

Nun sei aber an die Schlange oben erinnert: sie kann auch nicht Knicke „gehen“, weil sie einen bestimmten „Wendekreis“ nicht unterschreiten kann.

Oben hatte ich dazu gesagt:

In einer Kurve werden [...]


Nun hat ein Kunststoffstreifen zwar keine Rippen, sein Verhalten erkläre ich mir aber

(als Auch-nur-Laie)

ganz ähnlich. Mal angenommen, der noch nicht gebogene Kunststoffstreifen sieht vergrößert so aus:

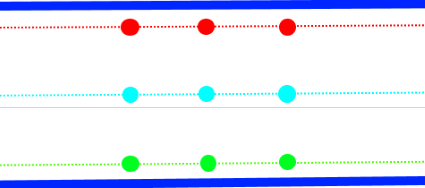
Dabei seien die Punkte Materieteilchen in gleichem Abstand.

Jetzt endlich kommt die bereits im Titel genannte „Spannkraft“ ins Spiel: für unser Experiment brauchen wir

wurde:

    entspannter
Ausgangszustand		 maximal
zusammengedrückt		 maximal
auseinandergezogen
 

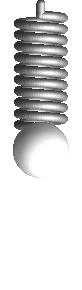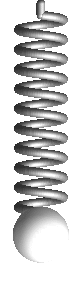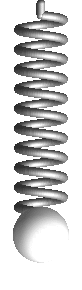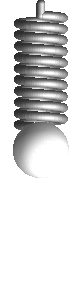 Unser Kunststoffstreifen muss also

Was nun beim Biegen eines solchen „Druck- und Zug“-Kunststoffstreifen  passiert, lässt sich nun in der Tat mit Druck- und Zugfedern illustrieren.

Dazu montieren wir entspannte Federn zwischen die Punkte in  und erhalten:

 

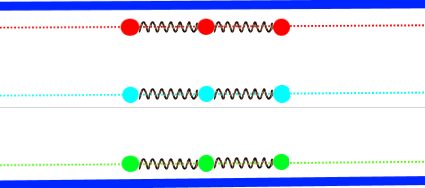
(Am besten baut man mal einen großen Mechanismus, mit dem man das von Schülern untersuchen lassen kann.)


Wenn wir nun den Kunststoffstreifen biegen, passiert Folgendes:

→

  →

  →

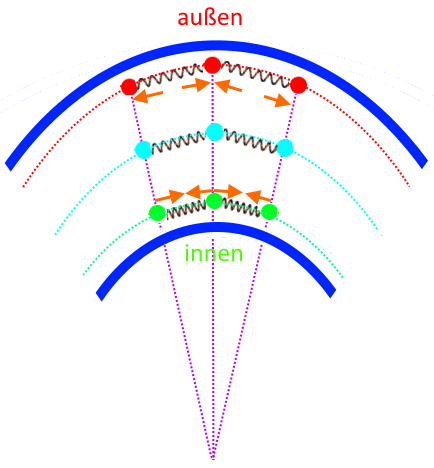
Wenn der Kunststoffstreifen nicht in dieser gebogenen Position festgehalten wird, versucht er nun aber, wieder so gerade wie vorher zu werden. Und das funktioniert so:

 →

und ziehen die Punkte wieder aufeinander zu.

  →

und schieben die Punkte wieder auseinander.

Damit aber können wir nun erklären, weshalb der Kunststoffstreifen sich nicht wie der geknickte Papierstreifen in  verhält, sondern annähernd (?) wie der Funktionsgraph.

Vorgabe ist natürlich, dass der Kunststoffstreifen durch alle im Folgenden eingezeichneten Punkte geht:

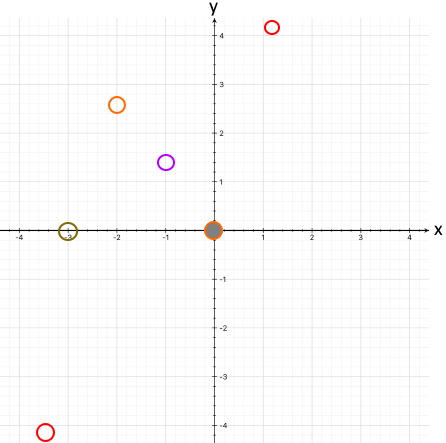
Angenommen also mal, wir würden den Kunststoffstreifen mit roher Gewalt

(aber ohne dass er Schaden nimmt; s.o.)

auf den kürzest möglichen Weg durch alle Punkte ziehen:

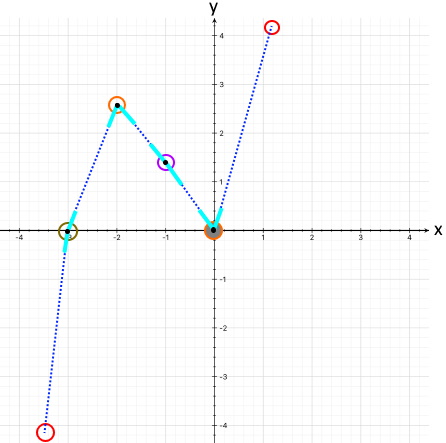
Dann würden

(mathematisch gesagt: Nicht-Differenzierbarkeits-Stellen)

auftreten,

(fast hätte ich gesagt: möglichst gerade)

zu werden, und spreizt er sich wieder möglichst weit auf:

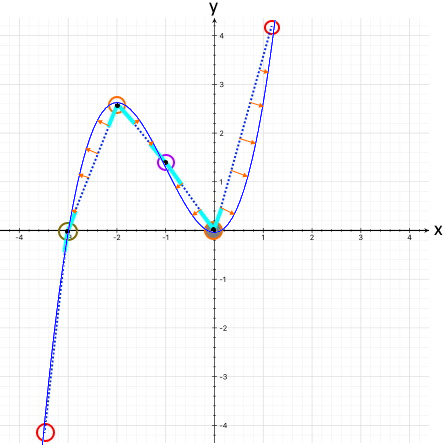
 Man könnte auch sagen: der Kunststoffstreifen sucht einen Kompromiss zwischen

und dieser Kompromiss ist eben annähernd (?) der Funktionsgraph.

So ganz nebenbei beseitigt der Kunststoffstreifen auch die (mathematisch) unschönen Knicke.

Zuguterletzt wette ich, dass Ingenieure sogar "irgendwie" (?) berechnen könnten, wie genau der gebogene Kunststoffstreifen aussieht - und ob er exakt mit dem Funktionsgraphen von y = x3 + 2x2  übereinstimmt.

PS: Das Klebestreifen-Verfahren funktioniert (!) auch für andere Funktionen erstaunlich gut:
PPS: oben hatte ich behauptet, dass es auch einem neunmalklugen Mathematiker unmöglich sei, alle Rechnungen zu überschauen, die
  • von den vier Bedingungen 2., 3., 4. und 5.
  • zu den Ergebnissen  , b = 2 , c = 0 und d = 0
  • und damit zu der Funktionsgleichung y = x3 + 2x2 führen:


Aber stimmt das denn überhaupt?

Die Behauptung stimmt zumindest nicht oder nur halb für die Berechnung von c = 0 und d = 0

(und diese einfachen Ergebnisse machen im Folgenden dann auch die Berechnungen von a und b relativ einfach).

Schauen wir uns nämlich mal an, wieso die Berechnungen von c = 0 und d = 0 so einfach sind:
 

A. Berechnung von d :

Diese Rechnung ist offensichtlich wegen der vielen Nullen so einfach. Diese vielen Nullen rühren aber allein daher, dass der Funktionsgraph durch den Ursprung U ( 0 | 0 ) mit seinen beiden Null-Koordinaten 0 und 0 geht

(wofür wir den Schulbuchautoren schon zum ersten Mal dankbar sein können).

 

  

B. Berechnung von c :

  1. : weil aber zusätzlich f ' (0) = 0 ist, folgt c = 0
Diese Rechnungen sind offensichtlich ebenfalls wegen der vielen Nullen so einfach, für die es hier aber gleich zwei Gründe gibt:
  • die hellblau unterlegte 0 rührt wieder daher, dass der Funktionsgraph durch den Ursprung U ( 0 | 0 ) geht,
  • die hellviolett unterlegte 0 rührt hingegen daher, dass der Funktionsgraph dort die x-Achse berührt, also eine waagerechte Tangent und somit die Steigung 0 hat
(wofür wir den Schulbuchautoren zum zweiten Mal dankbar sein können).

Es war also von den Schulbuchautoren ausgesprochen freundlich
  • den Funktionsgraphen durch den Ursprung U ( 0 | 0 ) gehen
  • und dort die x-Achse berühren zu lassen.
Und weil das alles die Rechnungen so einfach macht, halten wir an diesen beiden Eigenschaften im Folgenden immer fest: egal, was passiert, es gilt: der Funktionsgraph hat im Ursprung eine waagerechte Tangente bzw.

.

Noch an einer anderen Stelle der Rechnungen taucht eine Null auf, die die Rechnung

(jetzt allerdings nur noch ein wenig),

nämlich in


Diese kleine Vereinfachung liegt daran, dass auch P auf der x-Achse liegt, also die y-Koordinate 0 hat.

Hier können wir also den Schulbuchautoren zum dritten Mal danken

(und mein Dank wird ihnen ewig nachschleichen, sie aber nie erreichen).

Auch diese kleine Hilfe nehmen wir im Folgenden gerne in Anspruch, indem wir
  • immer den Ursprung als Berührpunkt nehmen
  • und P entlang der x-Achse hin und her wandern lassen:



Auf diese Art sind dann z.B. folgende Funktionsgraphen dritten Grades möglich:



Aber wozu dieses Wandern von P, wo P doch eigentlich durch die Aufgabenstellung fest als P ( -3 | 0 ) vorgegeben ist?

Das liegt daran, dass wir oben bei den Berechnungen von  a und b mehrfach mit den Vorgaben -3 und 6 weitergerechnet haben:

Bei all diesem Weiterrechnen sind die Vorgaben -3 und 6 vollständig verschwunden, und deshalb können wir nicht mehr nachvollziehen,
  • wie sich die beiden Vorgaben  -3 und 6 durch die Rechnungen "geschlängelt" haben,
  • wie also aus ihnen und b = 2 entstanden sind.
Es kommt noch hinzu, dass wegen der Ableitungsregel für Potenzfunktionen auch noch die ehemaligen Exponenten 3 und 2 auf parallelen und damit kaum gleichzeitig überschaubaren Wegen in die Ergebnisse  und b = 2 eingehen:



Dieser Umstand macht das Nachverfolgen der Rechenwege aber besonders schwierig, da die beiden Exponenten 3 und 2 nichts mit den beiden Bedingungen 4. und 5. zu tun haben, aus denen die beiden Zahlen -3 und 6 stammen. Eine Verwandtschaft zwischen  -3 und 6 und 3 und 2 könnte man ja durchaus fälschlich vermuten:

  • -3 → 3
  • 6 = 3 • 2
Aus den genannten Gründen sieht die Berechnung der Endwerte und b = 2 aus den Anfangswerten -3 und 6 doch etwa so aus
(obwohl sich die Anfangs- und Endwerte doch sehr ähneln):


Um all diese schwierigen Verwirrungen aufzulösen und sozusagen den


gordischen Knoten zu zerschlagen,

müssen wir dafür sorgen, dass sich die Anfangswerte
  •         x  (ehemals -3 )
  • und  y  (ehemals  6 )
so durch die Rechnungen durchschlängeln, dass niemals Gefahr besteht, sie mit anderen Zahlen zu vermischen.

Dazu machen wir alles

(ein typischer mathematischer Weg)

  • erstmal schwieriger
  • um es hoffentlich später sehr einfach machen zu können.
Da es doch zumindest ungewohnt ist, mit Kästchen zu rechnen, nennen wir
  •          x   nun   t 
  • und    y  nun  s .
Anders gesagt:
  • statt von P ( -3 | 0 ) sprechen wir nun allgemein von P (  t  | 0 )
  • und  s   soll die Steigung des Funktionsgraphen in P (  t  | 0 )  sein
Damit erhalten wir folgende Rechnungen:


(Nebenbei:
  • die Gleichung  funktioniert
  • auch für positive  t , also wenn P (  t  | 0 ) rechts vom Ursprung liegt,
  • sowie für negative  s   , also negative Steigungen (Gefälle),
  • aber nicht für  t   = 0 , wenn also P im Ursprung liegt, denn für t   = 0 würde sowohl in als auch in durch Null geteilt:
  • Wenn wir das Ergebnis überprüfen, indem wir wieder die ursprünglichen Werte 6 und -3 für  s  und  t  einsetzen, so erhalten wir tatsächlich die in der anfänglichen Aufgabenstellung gesuchte Funktionsgleichung y = x3 + 2x2 !)

Aber nochmals zu unseren beiden Ergebnissen und :
  • hier können wir nun endlich sehen, wie sich die Anfangswerte  s  und  t  in den Endwerten und niederschlagen,
  • aber es ist wohl auch der Nachweis erbracht, dass niemand mit einem göttlichen Blick überschauen kann, wie sich die Anfangswerte  s  und  t  zu den Endwerten und durgeschlängelt haben.

Es ist wie

 :

man

  • versteht vielleicht jeden Einzelschritt,
  • hat aber keinen Überblick über den Gesamtverlauf.

Oder es ist wie ein Blindflug, bei dem Standardrechnungen und mathematische Notwendigkeiten der Leitstrahl sind, aber auch ein (manchmal falsches) Versprechen, dass man eine Lösung finden wird:


"Am Ende der dunklen Gasse
erstrahlt die Gelbe Wand."

Es bleibt aber der Eindruck , und die Hoffnung auf eine Vereinfachung ganz am Ende hat sich wohl gründlich zerschlagen.

Nun ist die Rechnung mit   s  und  t  ja noch relativ einfach: es gibt in der anspruchsvollen Mathematik erheblich längere und komplexere Rechnungen (und Beweise!), die nun wahrhaft kein Mensch mehr komplett überschauen kann.

(Vgl. z.B.  : ein Beweis, bei dem ich gar nichts verstehe
[den ich aber trotzdem oder gerade deswegen bewundere].
Aber ich vermute mal, dass sogar sein Schöpfer Andrew Wiles ihn nicht komplett überschaut.

Ich vermute mal, der Beweis ist wie die hochkomplexe Partitur einer Symphonie
,
allerdings mit dem kleinen Unterschied, dass nichtmal der Komponist [wie Beethoven oder Mozart] bzw. Dirigent alle Stimmen gleichzeitig im Kopf hat.

Nebenbei: Auswendig-Können bedeutet noch lange nicht Verstanden-Haben.)

Allerdings es nicht eindeutig ein Nachteil, wenn man lange Rechnungen nicht komplett überschaut, sondern hat es für Mathematiker durchaus einen ganz eigenen Reiz

(den viele Laien noch nie erfahren haben und der ihnen daher völlig fremd ist):

Mathematiker sind wie Trapper im wilden Westen , die sich einen Weg durch unwegsames Gelände suchen: da hilft keine „Brechstange“, und man kann sich den Weg auch nicht einfach freischlagen oder planieren  , sondern muss sich raffiniert und geschmeidig

(ein gelungener Beweis ist immer auch elegant: )


dem Gelände und seinen Gegebenheiten, d.h. den mathematischen Notwendigkeiten anpassen und dem Automatismus der Rechnungen vertrauen:

 

"The long and winding road
That leads to your door
Will never disappear
I've seen that road before
It always leads me here
Lead me to you door"
(The Beatles)

Oft gibt es aber auch in der Mathematik nicht nur einen Weg zum Glück, sondern verschiedene

(darunter steinige, relativ bequeme, gefährliche, herausfordernde, langweilige, steile, umständliche, atemberaubende, schöne ...):

Es ist also nicht alles Automatismus (und Zwang), sondern es gibt durchaus auch in der Mathematik viele Freiheiten.

Der größte Reiz ist es aber natürlich, als Erster das Gelände zu „meistern“ - und einen Gipfel zu erklimmen

(oder zwar nicht der Erste zu sein, aber sich immerhin sagen zu können: ich hab‘s selbst geschafft):

Und in der Mathematik gibt‘s viele Berge, auf denen noch keiner war (vgl. ) :

(Unter massivem Einsatz von Mathematik ist man da aber immerhin schon drüber geflogen.)

Ich war noch nie ein begnadeter Mathematiker

(sondern "nur" Mathematiklehrer),

und deshalb reicht es mir, den toppfitten jungen Bergsteigern zuzuschauen und zu überlegen, wie sie auf die Berge gekommen sein mögen:

Nur eines gilt auch für die Mathematik: wer die Dschungel und Berge scheut oder bereits nach der ersten leichten Steigung aufgibt, sollte zuhause auf dem Sofa bleiben und sein Leben lang RTL gucken.