 )
)warum Steckbriefaufgaben "Steckbrief"-Aufgaben heißen
|
„»Hier, sehen Sie sich die an, Chef«, sagte Moers und fächerte wie
Spielkarten eine Reihe Fotografien vor ihm auf.
Was er da allein in seiner Kammer geleistet hatte, war hervorragende
Arbeit. Ausschließlich anhand der vagen Personenbeschreibungen, die
man ihm geliefert hatte, war es ihm gelungen, drei Menschen
regelrecht zum Leben zu erwecken: den dickleibigen, braunhaarigen
Ausländer, der sich übertrieben elegant kleidete, die junge Frau mit
dem weißen Hut und schließlich den Komplizen, der an einen
Straßenverkäufer obszöner Ansichtskarten erinnerte.“
(Quelle:
 ) ) |
Keine Ahnung, ob der Steckbrief
 echt ist:
echt ist:

(ein
spiegelverkehrter Ausschnitt dieses Fotos ziert den Steckbrief
 ),
),
aber es scheint mir doch unwahrscheinlich, dass damals auf Steckbriefen schon Fotos möglich waren.
Interessanter für uns ist sowieso die bildlose
(und deshalb wohl eher echte)
Steckbriefvariante  : da hat (haben) ein oder mehrere Zeuge(n) wirklich mal Billy the Kind
gesehen und mehr oder minder treffend einige seiner Merkmale genannt:
: da hat (haben) ein oder mehrere Zeuge(n) wirklich mal Billy the Kind
gesehen und mehr oder minder treffend einige seiner Merkmale genannt:
 |
Mit diesem doch arg vagen Raster und vielleicht sogar
einer ungefähren (falschen?) visuellen Vorstellung
 im Kopf schwärmen nun
Heerscharen von Sheriffs
im Kopf schwärmen nun
Heerscharen von Sheriffs  und Kopfgeldjägern
und Kopfgeldjägern
 aus und messen ihnen begegnende Menschen an diesem Raster
aus und messen ihnen begegnende Menschen an diesem Raster
(besser nicht allzu genau hinschauen, sondern vorsorglich als erster schießen):
 |
Zusammengenommen also
 |
bzw.
| |
In der Mathematik gibt es das genauso:
Funktionsgleichung
![]() Merkmale des
Funktionsgraphen :
Merkmale des
Funktionsgraphen :
das Verfahren, mit dem man
sucht
(u.a., um eine Vorstellung von der als Funktionsgleichung doch arg abstrakten Funktion zu bekommen),
nennt man „Kurvendiskussion“
(warum eigentlich?).
Bei dieser Kurvendiskussion werden standardmäßig einige ebenso relativ leicht zu berechnende und markante Punkte (Merkmale) des Funktionsgraphen gesucht, nämlich insbesondere
Ein Beispiel:
| y = 2x3 - 3x2
+ 1
|
(... wobei sich schon einige Leute totprobiert, weil niemals eine Lösung gefunden haben).
Üblicherweise probiert man für x die Zahlen 0, 1, 2, -1 und -2 aus
(und wenn man dann noch immer nichts gefunden hat, pfeift man auf die Lösung und macht Feierabend).
Im vorliegenden Fall haben wir aber schon für x = 1 Glück, denn
2 • 13 - 3 • 12 + 1 =
= 2 • 1 - 3 • 1 + 1 =
= 2 - 3 + 1 = 0 .
Wir erhalten also die erste Nullstelle N1 ( 1 | 0 ).
Mit hier nicht vorgeführter Polynomendivision können wir dann noch die zweite Nullstelle N2 ( - 0,5 | 0 ) finden.
f (x) = 2x3 - 3x2 + 1 ⇒ f ' (x) = 6x2 - 6x .
(notwendige Bedingung):
6x2 - 6x = 0
⇔ (6x - 6) • x = 0
⇔ 6x - 6 = 0
oder x = 0
(vgl.
![]() )
)
⇔ 6x = 6 oder x = 0
Zu den beiden Lösungen 1 und 0 kennen wir von oben schon die y-Koordinaten, nämlich y = 0 und y = 1.
Mögliche Minima oder Maxima sind also M1 ( 1 | 0 ) = N1 ( 1 | 0 ) und M2 ( 0 | 1 ) = Sy ( 0 | 1 ) .
Jetzt sparen wir uns die zweite Ableitung
(hinreichende Bedingung)
und machen wir es uns sehr einfach: weil die Funktion f dritten Grades ist und da M1 tiefer als M2 liegt
(nämlich M1 den kleineren y-Wert hat),
ist
Insgesamt haben also erhalten:
y = 2x3 - 3x2
+ 1
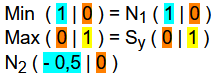 |
Mit all den berechneten Punkten (Merkmalen) haben wir schon eine gute Vorstellung von dem Funktionsgraphen:
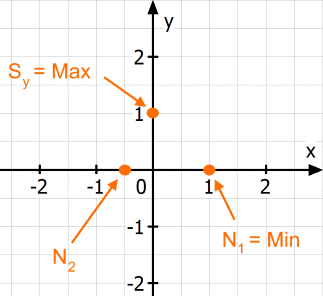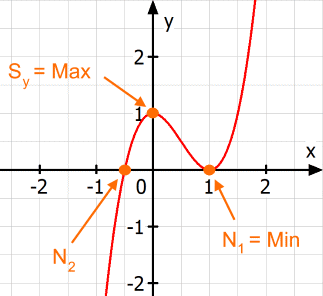
Wir erhalten also durch die
Kurvendiskussion
y = 2x3 - 3x2
+ 1
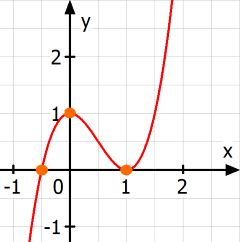 . . |
Funktionsgleichung
![]() Merkmale des
Funktionsgraphen :
Merkmale des
Funktionsgraphen :
Ein Beispiel:
vorgegeben seien wegen der Einsen und Nullen besonders einfache Merkmale des (ansonsten unbekannten) Funktionsgraphen einer Funktion dritten Grades:
Gesucht ist die passende Funktionsgleichung, also
Funktionsgleichung ?
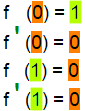 |
Immerhin wissen wir schon eines von der Funktionsgleichung: da die gesuchte Funktion dritten Grades ist, muss ihre Funktionsgleichung die (jetzt noch allgemeine) Form
f(x) = ax3 + bx2 + cx + d
haben.
Da unter den Merkmalen auch Ableitungen sind, berechnen wir vorsorglich sofort f ' (x) = 3ax2 + 2bx + c
("was man hat, das hat man").
Wenn wir nun die o.g. „Merkmale“ in die allgemeine Funktionsgleichung bzw. deren Ableitung übersetzen, erhalten wir
Die dadurch entstandenen Gleichungen
sehen nun zwar erstmal furchteinflößend aus, werden wegen der einfachen Zahlen 0 und 1 aber doch schnell viel einfacher:
Oder kurz:
Daran sind höchstens noch die Gleichungen (C) und (D) schwierig, aber auch diese werden immerhin schon ein bisschen einfacher, wenn wir in sie
⇒ 0 = a + b + 1 (E)
⇒ 0= 3a + 2b (F)
Oder kurz:
Das sind zwei Gleichungen mit jeweils zwei Unbekannten a und b Jede einzelne Gleichung ist nicht eindeutig lösbar, weil wir jeweils nur eine Abhängigkeit zwischen a und b erhalten.
Aber machen wir doch aus der Not eine Tugend und schauen wir uns an, wie in Gleichung (E) das a vom b abhängt:
0 = a + b + 1 | - b - 1
⇔- b - 1 = a bzw. a = - b - 1 (G)
Wenn wir in (F) für a nun - b - 1 einsetzen, erhalten wir
0 = 3•( - b - 1 ) + 2b,
und das ist nun endlich eine einzige Gleichung mit der einzigen Unbekannten b, die wir nun berechnen können:
0 = 3•( - b - 1 ) + 2b
⇔ 0 = 3•( - b ) - 3•1 + 2b
⇔ 0 = - 3 b - 3 + 2b
⇔ 0 = - b - 3 | + b
⇔ b = - 3
Wenn wir in (G) für b nun - 3 einsetzen, erhalten wir zuguterletzt auch
a = - (-3) - 1 = 3 - 1 = 2
oder kurz a = 2.
Damit haben wir insgesamt a = 2, b = - 3, c = 0 und d = 1 und somit die Funktionsgleichung y = 2x3 - 3x2 + 1 .
Oder kurz:
y = 2x3 - 3x2
+ 1
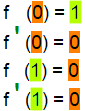 |
Die Funktionsgleichung y = 2x3 - 3x2 + 1 sollte uns aber von oben bekannt sein, weshalb wir auch schreiben können:
 |
(... wobei ergänzt sei, dass bei Funktionen dritten
Grades
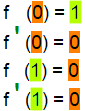 und
und
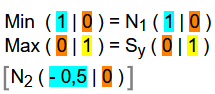 dasselbe bedeuten und
dasselbe bedeuten und
![]() sowieso nur eine
unnötige Zusatzinformation ist.)
sowieso nur eine
unnötige Zusatzinformation ist.)
Weiteres zu Steckbriefaufgaben:
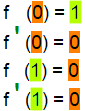 sind aus drei
Gründen besonders einfach:
sind aus drei
Gründen besonders einfach:(vgl. oben z.B.
1 = a•03
+ b•02
+ c•0
+ d
⇒ 1 = a•0
+ b•0
+ c•0
+ d
⇒ 1 =
0 +
0 +
0 + d
⇒
1=
d );
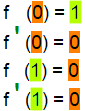 sind alle bereits
in mathematischen Gleichungen formuliert, während in vielen
anderen Steckbriefaufgaben sprachliche Umschreibungen benutzt werden, die überhaupt
erst in Gleichungen zu übersetzen sind;
sind alle bereits
in mathematischen Gleichungen formuliert, während in vielen
anderen Steckbriefaufgaben sprachliche Umschreibungen benutzt werden, die überhaupt
erst in Gleichungen zu übersetzen sind;
die sprachliche Umschreibung von
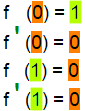 könnte z.B.
lauten: "der Graph einer Funktion dritten Grades geht durch die Punkte P ( 0 | 1
) und Q ( 1 | 0 ) und hat in beiden Punkten waagerechte Tangenten";
könnte z.B.
lauten: "der Graph einer Funktion dritten Grades geht durch die Punkte P ( 0 | 1
) und Q ( 1 | 0 ) und hat in beiden Punkten waagerechte Tangenten";
(wie im Beispiel eben)
von gegebenen Punkten und waagerechten Tangenten, sondern z.B. von der Steigung einer "Wendetangente"
(Tangente in einem erst zu berechnenden Wendepunkt und damit f ' (x) für den Fall, dass f '' (x) = 0)
die Rede ist;
einen schönen Überblick über das Instrumentarium
der Folterwerkzeuge  , die gerne in Klassenarbeiten und Abiturklausuren gepackt werden, liefert
folgende Liste:
, die gerne in Klassenarbeiten und Abiturklausuren gepackt werden, liefert
folgende Liste:
(Es ist allemal empfehlenswert, diese Liste häufig hin- und herzuübersetzen.)
Ein Beispiel: eine Firma entwickelt eine Rutsche
für kleine Kinder. Die Rutsche soll ungefähr so aussehen:

Von der Seite gesehen:
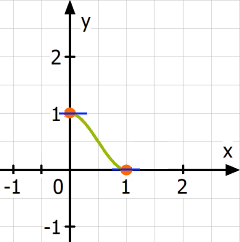
Da dienen die waagerechten Tangenten dazu, dass die Rutschbewegung oben langsam anfängt und unten langsam endet.
Geeignete Steckbrief-Merkmale sind da
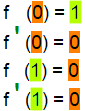 , womit die
Rutsche ein Ausschnitt des Funktionsgraphen
, womit die
Rutsche ein Ausschnitt des Funktionsgraphen
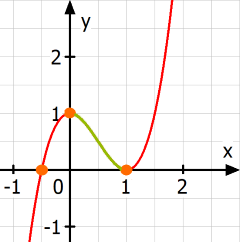 der Funktion mit der Funktionsgleichung y = 2x3 - 3x2
+ 1 ist (s.o.).
der Funktion mit der Funktionsgleichung y = 2x3 - 3x2
+ 1 ist (s.o.).
Oh Wunder über Wunder, dass Mathebücher und -lehrer (wenn sie fair sind) immer exakt so viele mathematische Merkmale nennen
(der Rest ist nicht-mathematische Verpackung in eine Anwendung),
wie zur Bestimmung der Funktionsgleichung benötigt werden, also keins zu viel und keins zu wenig. Das bedeutet aber, dass man zur Lösung von Steckbriefaufgaben alle mitgelieferten mathematischen Merkmale benutzen muss.