Vormerkungen
Hauptteil

Vorbemerkungen

• Hier sei mal davon abgesehen, dass die Tafel oder das "Smart[!]board" auch in anderen Schulfächern benutzt wird, die vielleicht ganz andere Anforderungen an diese Geräte haben: mich interessieren diese Geräte hier nur im Hinblick auf das Schulfach Mathematik.

• Eines hat die gute alte Tafel aber all den "Smartboards" in allen Schulfächern voraus:

  • sie ist vergleichsweise spottbillig

(Tafel ca. 1000 €, "Smartboard" mit Beamer mindestens 3000 €, pro Klassen-/Fachraum, und das ca. alle zehn Jahre; da jubeln die "Smartboard"-Hersteller - und sowieso Microsoft),

• und im Gegensatz zu "Smartboards" unverwüstlich:

• da "Smartboards" Hightech-Produkte sind, sind sie spätestens nach zehn Jahren total veraltet;

• "Smartboards" sind wie alle elektronischen Produkte fehleranfällig, sei's aufgrund technischer Probleme (z.B. funktioniert das Schulnetz mal wieder nicht), sei's aufgrund menschlicher Fehler (der ach so dummen Laien [Lehrer]). 

• Tafeln sind im Gegensatz zu "Smartboards" idiotensicher in der Handhabung - und nichts lenkt vom Fachlichen ab.
• Ich leugne nicht, dass ein "Smartboard" auch im Mathematik-Unterricht viele Vorteile ggb. der Tafel hat. Aber mich interessieren im Folgenden nur die Vorteile der guten alten Tafel. 
• Natürlich ist auch in der Mathematik der Einsatz von Computern und Multimedia sinnvoll:

• in der Schulmathematik beispielsweise beim Einsatz von
• erstklassigen Mathematikfilmen

(vgl.  ; diese Mathematikfilme [auch auf Youtube] sind den meisten Lehrern völlig unbekannt - und teilweise besonders gut geeignet, um Schülern zu vermitteln, was Mathematik überhaupt "ist"

[wofür man allerdings im streng durchgetakteten lehrplangemäßen Unterricht kaum Zeit hat]),

(Von wegen "Haben Sie sich auch schon mal gefragt ...": hat der Laie [Schüler] natürlich nicht.)

(Mir war bislang leider unbekannt, dass es mit   inzwischen ein [kompliziert zu handhabendes] Computerprogramm gibt, das bei mathematischen Beweisen hilft!)

• Eine Tafel ist erst richtig eine Tafel, wenn sie
•  nicht mehr "jungfräulich" ist ,
• sondern auch nach dem Abwischen noch Spuren früherer Arbeit zeigt   und es so richtig schön kreidestaubt.

Hauptteil

Manchmal überkommt einen als Mathematiklehrer das Gefühl, dass viele Schüler grundsätzlich nicht für den Reiz der Mathematik zugänglich sind

(so dass bei diesen Schüler jeder Versuch, Mathematik interessant zu vermitteln, "Perlen vor die Säume" zu sein scheint;

nebenbei: dass Schüler unzugänglich für den Reiz der Mathematik sind, ist nicht damit zu verwechseln, dass sie Mathematik grundsätzlich nicht können).

Vollends unverständlich mag es da erscheinen, dass Tafelbilder reizvoll sein können.

Und das insbesondere, weil Schüler meistens lieblos hingerotzte und vollends chaotische Tafelbilder erleben - so dass Tafelbilder geradezu der Inbegriff der Unverständlichkeit sind:

Kommt hinzu, dass die klassische staubige grüne Kreidetafel in der Zeit von "Smartboards" hoffnungslos zu sein scheint: worauf die Mathematiker in fröhlicher Altersweisheit pfeifen:

	( ; der Sprecher in dem Filmausschnitt ist der Direktor des  , und das wiederum ist eine der weltweit führenden Mathematik-Institutionen)
	„Wenn man die Mathematik auf ein Geräusch reduzieren soll, dann ist es dieses Klacken der Kreide auf der Tafel. Ruochuan Liu steht im Hörsaal des Hausdorff Centers in Bonn und entwickelt seine Formeln auf vier großen Tafeln. Routiniert greift der chinesische Mathematiker immer wieder zum Schwamm, nach einer Stunde hat er zwanzig Tafelbilder erstellt. Das Publikum im einzigen deutschen Exzellenzzentrum für Mathematik hört dem Redner gespannt zu. Doktoranden schreiben mit, viele Professoren versuchen, Lius Gedanken nachzuvollziehen. „Tafeln wirken heutzutage altmodisch, aber sie sind für die Mathematik besser", sagt Peter Scholze, Professor am Hausdorff Center und Organisator des Expertentreffens. Er lieb es, wenn eine Theorie ganz klassisch mit Kreide Schritt für Schritt vorgestellt wird. Das erleichtere den Zugang zu der Gedanken eines Kollegen im Gegensatz zu fertigen Folien. Die Tafel ist die große Bühne für die Mathematik […]“ (Quelle: )

Genau das müssen Schüler eben auch lernen: selbst bei kompliziertester Mathematik bedarf es erstaunlicherweise oftmals

• nur einer Old-School-Tafel
• oder eines Blattes Papier und eines stinknormalen Bleistifts: .

Es gibt einen guten Grund für diese Position der Mathematiker:

• Mathematik ist eine oftmals arg verkürzte Sprache
• mit ganz eigenen Buchstaben

(z.B. der Zahl ),

Wörtern und Sätzen

(z.B.  a² + b² = c² beim Satz des Pythagoras)

,

• die ab und zu zwecks Veranschaulichung mit Bildern illustriert wird ,
• aber keinen multimedialen Schnickschnack braucht, sondern es reichen Tafel und Kreide (wenn man mit anderen kommuniziert) oder Papier und Stift (wenn man alleine vor sich hinbosselt).

(Es gibt zwar auch mathematische Einzelkämpfer

[z.B. Andrew Wiles , der   bewiesen hat; vgl. auch den unbedingt empfehlenswerten Film ],

aber Mathematik entsteht meistens in stetem Austausch mit Fachkollegen.)

• Selbst wenn später ein Computer an einen Beweis gesetzt wird, werden die grundlegenden Gedanken für das Computerprogramm meistens erstmal auf einer Tafel oder Papier entwickelt.

Aus all dem folgt: die guten alten Tafeln sollten unbedingt erhalten bleiben, wenn (zusätzlich) "Smartboards" in die Klassenzimmer eingebaut werden.

(Die "Smartboards" werden einfach vor die Tafeln gestellt und können ggf. auf Rollen weggefahren werden.)

Wie schön (!) aber mathematische Tafelbilder sein können, hat Jessica Wynne in ihrem Buch gezeigt:

Nur einige Beispiele aus diesem Buch:

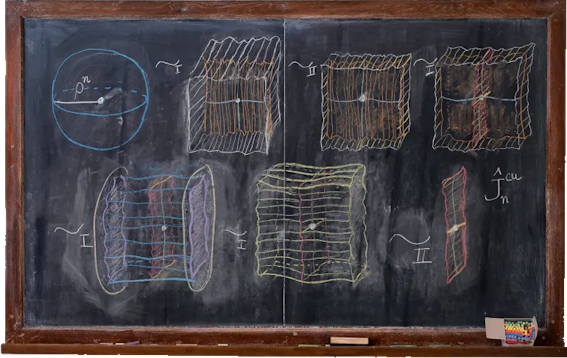
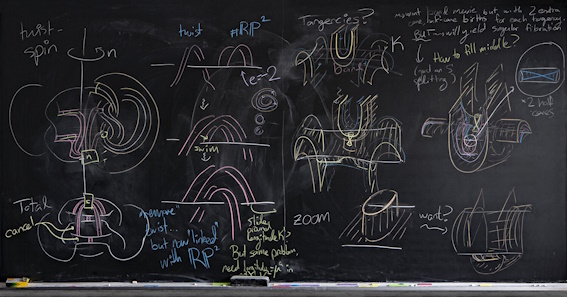
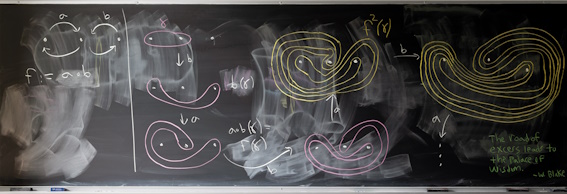
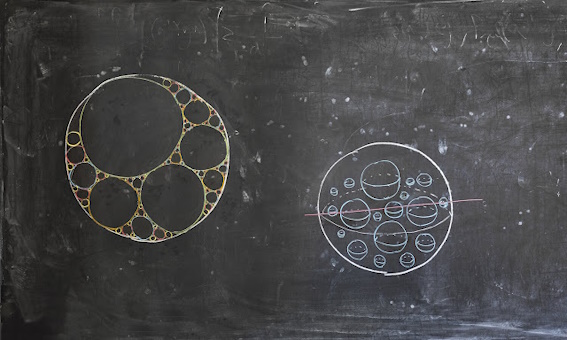
PS:

solche Tafelbilder können für Lehrer Vorbilder und Herausforderungen sein. Ich muss allerdings gestehen, dass meine Tafelbilder früher eher dahingeschludert waren. Einmal hatte ich allerdings das Glück, dass eine Kollegin (V.L.) immer in den Stunden vor "meinem" Grundkurs Mathematik einen Grundkurs im selben Jahrgang unterrichtet hat. Ihre Tafelbilder waren immer derart vorbildlich, dass ich sie immer gebeten habe: , damit ich in den Stunden danach anhand ihrer Tafelbilder unterrichten konnte.

PPS:

Mathematiker*innen bei der Arbeit: