der schönste Beweis aller Zeiten

D) Folgerungen und Einordnung

Fragt man einen Techniker, was ist, nimmt der seinen Taschenrechner und sagt: 1,414214.

Der Physiker sagt einfach: Ja, so ungefähr 1,41.

Der Mathematiker geht weg, kommt nach zwei Stunden wieder und sagt: Ich weiß zwar nicht, wieviel ist, aber ich kann beweisen, dass es sie gibt.

Der Beweis wurde das erste Mal von

Euklid
(ca. 360 - 300 v. Chr.)

in seinem berühmten Buch "Die Elemente" veröffentlicht (wobei unklar ist, ob er ihn auch erdacht hat).

Newtons Ausgabe der "Elemente" des Euklid
mit Newtons handschriftlichen Randanmerkungen

Euklids Buch "Die Elemente" ist eins der meistgedruckten Bücher aller Zeiten und sicherlich das meistgedruckte Mathematikbuch aller Zeiten. Es blieb über 2000 Jahre in Gebrauch und das absolute Standardwerk, weil es als erstes Buch überhaupt die Mathematik systematisch aufarbeitete und damit der Maßstab für alle folgenden Mathematikbücher wurde.

Unter "systematisch" ist dabei zu verstehen, dass 

• alles nacheinander aus ganz wenigen Grundannahmen (sogenannten unbeweisbaren bzw. selbstverständlichen Axiomen) gefolgt wurde und

• immer auf eine Annahme ein Beweis folgte.

Die "Elemente" waren auch in der Hinsicht richtungsweisend, dass in ihnen erstmals ein abgenagter mathematischer Beweisstil entwickelt wurde: da ist kein Platz mehr für Persönliches, Irrwege, aber auch längere Erklärungen, da herrscht nur noch die eiskalte logische Folgerung.

Der Beweis hinterlässt einen äußerst zwiespältigen Eindruck:

• Einerseits ist er eigentlich ganz einfach, nur kommt man andererseits wohl gerade an den einfachsten Stellen (z.B. 2 · q² = p²   p ist gerade) nicht von selbst drauf.

• Man kann vermutlich alle Einzelschritte des Beweises verstehen, aber man bekommt keinen Gesamteindruck; ja, am Ende fühlt man sich mit der falschen anfänglichen Annahme, dass rational sei, geradezu reingelegt und als dumm verkauft.

Dessen muss man sich keineswegs schämen, denn das ist immerhin z.B. auch dem großen Philosophen

Arthur Schopenhauer
(1788 - 1860)

bei der Mathematik so ergangen.

Oder mit

Heinrich Hertz
(1857 - 1894)

schon positiver, staunender formuliert:

"Man wird das Gefühl nicht los, daß diese mathematischen Formeln eine unabhängige Existenz und ihre eigene Intelligenz haben, daß sie gescheiter als wir sind, ja sogar gescheiter als ihre Entdecker, daß wir mehr aus ihnen errechnen, als wir ursprünglich hineinlegten."

• Der Beweis wirkt aus mehreren Gründen geradezu hinterhältig:

• die sogenannte "indirekte" Beweisart (hier erstmals in der Geschichte!): (falsche) Annahme - Widerspruch - die Annahme muss falsch gewesen sein - man hat also das glatte Gegenteil der Annahme bewiesen.

Hätte man da nicht gleich ehrlicher die Annahme (dass irrational ist) beweisen können?

Genau da liegt das Problem: zumindest meines Wissens gibt es keinen direkten, sondern eben nur den indirekten Beweis.

Und immerhin folgt der indirekte Beweis der vermutlichen Geschichte: man wusste gar nicht, dass es auch irrationale Zahlen geben könnte, und ist deshalb (wie Pythagoras!) durchaus überzeugt davon ausgegangen, dass rational sei.

Und daran hat man dann so lange rum rumgeknobelt, bis eine bestimmte Rechnung (die oben!) zum Widerspruch führte, mit dem man erst gar nicht umzugehen wusste, aus der man dann aber dennoch wohl über übel die Konsequenz ziehen musste, dass die  wohl doch irrational ist, es also irrationale Zahlen gibt.

• Die zweite Hinterhältigkeit des Beweises liegt darin, dass er eben nicht die Existenz der beweist, sondern nur zeigt, dass sie nicht rational ist. Solch ein Vorgehen wirkt ausgesprochen negativ-destruktiv: ich zeige nur, was nicht geht, nicht aber, was geht.

• Drittens ist an dem Beweis hinterhältig, dass er nicht im mindesten zeigt, was denn nun eigentlich konkret und vorstellbar ist. Er liefert keinen einzigen Hinweis darauf, wie weitere Dezimalstellen von aussehen könnten.

Der Beweis ist sogar noch erheblich destruktiver: 

Wenn gilt

jede rationale Zahl ist gleichermaßen sowohl als Bruch aus ganzen Zahlen als auch in Dezimal(stellenwert)schreibweise als hinter dem Komma endliche  oder periodische Zahl schreibbar.

und wenn zudem bewiesen ist, dass   nicht rational ist,

dann gibt es für

1. KEINE  Bruchschreibweise mehr,

2. keine exakte Dezimalschreibweise mehr

(jede endliche Näherung ist, weil eben endlich, auch schon ungenau - wenn auch vielleicht sehr nah dran).

Daraus folgt ganz prinzipiell (auch für die schlauesten MathematikerInnen): es gibt keine Chance, den Zahlenwert von   jemals ganz zu sehen.

Das EINZIGE, was wir über die mit absoluter Sicherheit wissen und jemals wissen werden, ist und bleibt (vgl. Erinnerung links oben): bzw.  "die ist diejenige (positive) Zahl, die mit sich selbst malgenommen (quadriert) 2 ergibt."

Wohlgemerkt: das ist kein Ergebnis, sondern so hatten wir von Anfang an definiert.

Und das ist und bleibt eine herzhaft unbefriedigende, weil indirekte Definition, etwa nach dem Motto

• "Regen ist, was die Straße nass macht" oder

• "gesucht ist diejenige Zahl, die mit 4 malgenommen 12 ergibt".

Solch indirekte Definitionen sind aber in der Mathematik durchaus üblich bzw. manchmal unumgänglich

(vgl. den Logarithmus:
log_a b ist diejenige Zahl, mit der ich a potenzieren muss, um b zu erhalten;
wenn also gilt c = log_a b, so muss gelten a ^c = b).

• dennoch leistet der Beweis in mehrfacher Hinsicht etwas Phantastisches:

• obwohl wir von den benutzten Variablen p, q und r nie Genaueres erfahren (außer dass sie normale bzw. gerade Zahlen sind), funktioniert der Beweis dennoch;

• gerade in seine indirekten Art zeigt der Beweis etwas sehr Merkwürdiges:

obwohl er nie von Dezimalzahlen (sondern von Brüchen) handelt, beweist er doch eine Aussage über sämtliche (unendlich viele!) Nachkommastellen von in Dezimalschreibweise:

• dass es eben unendlich viele sind und

• dass sie niemals periodisch werden.

Genau das aber ist schwer vorstellbar.

• So ganz nebenbei wird da außerdem bewiesen, dass wegen 

  ·= ()² =2

  das Produkt zweier irrationaler, also ganz scheußlich komplizierter Zahlen (nämlich beides mal ≈ 1,4142135623731) ganz einfach sein kann (nämlich die natürliche Zahl 2).

  Und das finde ich doch allemal erstaunlich: dass die unendlich vielen, unperiodischen Nachkommastellen letztlich doch "wissen", dass sie beim Multiplizieren exakt zu 2 zusammen passen müssen.

• Der Nachteil, dass wir nicht ganz genau wissen, was eigentlich (in Dezimalschreibweise) ist, ist gleichzeitig aber auch ein Vorteil:

wir sparen uns meistens sämtliche umständlichen Rechnungen mit der Dezimalschreibweise 1,4142135623731... (schalten auch gar nicht erst den Taschenrechner an!), sondern hantieren einfach mit dem Symbol rum (wovon wir nur eine einzige Sache wissen: dass das Quadrat exakt gleich 2 ist).

Das hat 1. den Vorteil, dass wir die ganze Zeit mit dem exakten Wert rechnen, sich also Rundungsfehler nicht unkontrolliert vergrößern können. 

(Z.B. ist der Rundungsfehler, wenn wir mit der Näherung 1,4 rechnen, bei 5 · 1,4 schon fünfmal so groß.)

Der zweite Vorteil ist, dass in vielen Rechnungen am Ende sowieso wieder quadriert werden muss und dann einfach wieder ()² =2 gilt.

Man schleppt also am besten möglichst lange un-ausgerechnet mit sich und fragt vielleicht erst ganz am Ende, was der Dezimalwert einer Gesamtrechnung ist.

Der Beweis der Irrationalität ist nebenbei nicht nur für die   möglich, sondern ganz ähnlich auch für die Wurzeln aus 3 und 5 und 6 usw., also aller natürlichen Zahlen, die nicht schon selbst Quadratzahl, also Quadrat einer ganzen Zahl sind (4; 9; 16; 25 ...) . Nur darf man dann nicht mehr mit der Teilbarkeit durch 2 bzw. geraden Zahlen argumentieren, sondern muss zur Teilbarkeit durch 3 oder 5 ...bzw. auch Primfaktoren übergehen.

Daraus aber folgt: da es unendlich viele natürliche Zahlen gibt, die nicht Quadratzahlen gibt, gibt es auch unendlich viele irrationale Zahlen. Kommt hinzu, dass auch die Wurzeln ganz anderer Zahlen (z.B. ) irrational sein können (aber nicht sein müssen; z.B. ist = , also rational). 

Es lässt sich sogar zeigen, dass es sehr viel mehr irrationale als rationale Zahlen gibt (und von letzteren gibt es schon unendlich viele!). Die berühmtesten unter ihnen sind die "Eulersche Zahl" e » 2,718281828 (eine Zahl, die merkwürdig oft bei natürlichen Prozessen vorkommt) und die "Kreiszahl" π ≈ 3,141592654.

Bei Wurzeln anderer Zahlen als 2 ist das Wurzelsymbol sogar noch viel nützlicher: ich habe zwar keinen blassen Schimmer, was der Dezimalwert z.B. der ist

(ich kenne, ehrlich gesagt, nicht mal seinen ganzzahligen Anteil, also seine ungefähre Größe, geschweigedenn die hinterletzten Nachkommastellen),

und doch kann ich wunderbar mit ihr rechnen. Z.B. weiß ich,

• dass ·exakt gleich 7293 ist oder

• dass 5 ·- 3 · = 2 ·.

Mit Wurzeln rechnet man also wie mit Variablen: man muss nicht wissen, welche Zahl sich hinter ihnen verbirgt, um mit ihnen hantieren zu können. Vgl. auch: ich muss nicht wissen, was in einem Paket drin ist, und kann doch rechnen: 5 Pakete - 3 Pakete = 2 Pakete.

Anlässlich der ersten irrationalen Zahl, also , zeigt sich auch, dass unsere frühere Vermutung, der Zahlenstrahl sei mit den rationalen Zahlen schon voll besetzt (man könne alle rationalen Zahlen mit einem durchgehenden Strich zeichnen), falsch war: es gab noch immer unendlich viele, wenn auch sehr kleine Lücken (eben die irrationalen Zahlen). 

Es lässt sich allerdings zeigen, dass der Zahlenstrahlen mit rationalen und irrationalen Zahlen zusammen nun tatsächlich lückenlos voll ist.

(Es gibt aber noch ganz andere, sogenannte "komplexe" Zahlen, die neben dem Zahlenstrahl liegen. Wenn man also [wieder mal] der Meinung war, mit den rationalen und irrationalen Zahlen nun wirklich alle Zahlen zu haben, so hat man sich [wieder mal] getäuscht. Entsprechend schwer fiel es [wieder mal] vielen MathematikerInnen, die neuen ["komplexen"] Zahlen anzuerkennen.)

Man bezeichnet die Menge der irrationalen Zahlen auch mit .

• die irrationalen Zahlen aus sind das glatte Gegenteil der rationalen Zahlen aus , d.h.

• eine Zahl ist

• entweder rational

• oder aber irrational, aber

• sie kann nicht beides gleichzeitig sein,

• und beide Mengen zusammen bilden die Menge der "reelen" Zahlen.

(Wenn ich einen durchgehenden Strich auf dem Zahlenstrahl zeichne, erwische ich jetzt endlich alle rationalen und alle irrationalen Zahlen.)

Offen ist bis hierhin noch die Frage, wie man denn nun Näherungen für die erhalten kann, also z.B. oben genannte 791 Nachkommastellen. Dazu hervorragend geeignet ist das "Heronverfahren", das zudem hübsch schnell gegen den exakten Wert von geht (vgl. das entsprechende Programm sowie auch die "Wurzel-Lupe" in der Programmsammlung ).

Der Beweis der Irrationalität ist in vielerlei Hinsicht aufschlussreich nicht nur für die Mathematik, sondern darüber hinaus für alle Wissenschaften:

• Um es mit Columbus zu vergleichen: als er lossegelte, war er (angeblich) der festen Überzeugung, dass er auf dem Weg nach Westen nur in Indien oder Japan  ankommen könnte. Da war es kein Wunder, dass er die von ihm entdeckten Inseln erstmal für Indien hielt (und dementsprechend die Bewohner der neuen Länder INDIaner nannte). Erst spätere Seefahrer haben dann herausgefunden, dass diese Inseln nicht zu Indien, sondern einem neuen Kontinent gehörten, den man dann Amerika nannte (nach einem anderen Entdecker namens Amerigo Vespucci). Columbus selbst aber hat zu seinen Lebzeiten nie erfahren, dass er tatsächlich einen neuen Kontinent entdeckt hatte. Die Anfangsannahme, dass man, wenn man westlich segelte, nur Indien oder Japan erreichen könnte, dass also auf dem Westweg kein Kontinent dazwischen lag (Rationalität), stellte sich also als falsch heraus. Und doch war diese falsche Anfangsannahme nicht überflüssig: obwohl sie falsch war, führte sie zu etwas Neuem, der Entdeckung Amerikas (Irrationalität). Ja, ohne die falsche Anfangsannahme (Indien, Rationalität) wäre vermutlich niemand auf die Idee gekommen, nach Westen zu segeln, wäre also Amerika (die Irrationalität) nicht entdeckt worden.

Die Entdeckung Amerikas wie die der irrationalen Zahlen ist dabei typisch für viele wissenschaftliche Entdeckungen: das Neue wurde oftmals nur "versehentlich" entdeckt bzw. dadurch, dass man das Alte konsequent zu Ende dachte und dabei seine Widersprüche bemerkte.

Allerdings: solche "Abfallprodukte der Forschung" erreicht in der Regel nur, wer lange genug am Alten rumgearbeitet hat. Ungeeignet für Neuentdeckungen ist allerdings meist auch, wer sich beim besten Willen nicht vorstellen kann, dass es auch noch anderes als das Gewohnte und ach so Anerkannte gibt, wer also schon allzu sehr im gängigen wissenschaftlichen Denken steckt.

• Mit der Irrationalität (unendlich vielen, meist unregelmäßigen Stellen hinterm Komma), aber auch der unendlichen Annäherung irrationaler durch endlich Zahlen (s.o. das Heronverfahren) wurde aber auch ein Tor in die Unendlichkeit aufgestoßen, das ca. 2000 Jahre nach Pythagoras zu einer ganz neuen Denkweise führte:

• der Differential- und Integralrechnung sowie dem Limes bei Newton und Leibniz,

• der Öffnung der "unendlichen Weiten des Weltalls" bei Nicolaus von Cues, Kopernikus und Giordano Bruno,

• der Öffnung des Horizonts durch Columbus, Magellan usw.

• Und zuguterletzt war der Beweis der Irrationalität das erste schöne Beispiel für Ideologiezertrümmerung: dass eine dreist eingeforderte Welterklärung (hier die des Pythagoras) als falsch überführt wurde.

Da widersprechen sich die Legenden teilweise:

• in der einen heißt es, Pythagoras selbst habe die Irrationalität bewiesen, das dann aber geheim gehalten;

• die andere besagt, einer seiner Schüler mit Namen Hippasos habe die Irrationalität ausgerechnet an einer Strecke im "Markenzeichen" der Pythagoreer, nämlich dem Pentagramm

, oder ausgerechnet mit dem "Satz des Pythagoras"

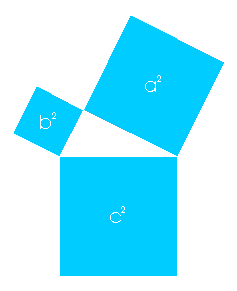
anhand der Quadratdiagonale in

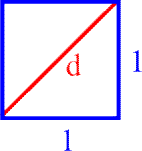
gezeigt - und Pythagoras habe ihn dafür umgehend ertränken lassen.

Spätestens hier sieht man, dass Pythagoras noch in einem ganz anderen Sinne "vorbildlich" für die gesamte Mathematikgeschichte war, in der ja keineswegs immer "rational", also vernünftig, sondern oftmals "irrational", d.h. unvernünftig oder zumindest nicht nach mathematischer Logik entschieden wurde.

(Man vergleiche nur mal, wie Cantor für seine Entdeckung der "Überabzählbarkeit" - und zwar durch Mathematiker! - fertig gemacht worden ist. Hauptstrippenzieher war da der durchaus bedeutende Mathematiker

Leopold Kronecker
(1823-1891),

der auch über 2000 Jahre nach erfolgtem Beweis der Irrationalität - und obwohl er sicherlich den Beweis bestens verstanden hatte - gesagt hat:

"Die ganzen Zahlen schuf der liebe Gott, alles übrige ist Menschenwerk."

"Es heißt, Kronecker habe einfach nicht an die Existenz irrationaler Zahlen geglaubt. Auch der Umstand, dass Kreise unvermeidlich zur Zahl führen, vermochte ihn nicht umzustimmen. Für Kronecker waren nur ganze Zahlen [und deren Brüche, also rationale Zahlen] real. Alles andere erachtete er für reine Einbildung.
Da heute jedes Kind auf einem Taschenrechner die Quadratwurzeltaste drücken und sich die Quadratwurzel von zwei ausgeben lassen kann (der unendliche Dezimalteil dieser irrationaler Zahl wird nach einer endlichen Zahl von Stellen abgebrochen und gerundet [und deshalb zeigt der Rechner eben nicht irrationale Zahlen an]), könnte man auf den Gedanken kommen, Kronecker - der nicht glaubte, dass es solche Zahlen gebe - müsse ein sehr armseliger Mathematiker gewesen sein. In der Tat war er aber ein ausgezeichneter Vertreter seines Fachs, dessen Name noch heute mit einer Reihe bedeutender mathematischer Resultate verbunden ist. Gerade der Umstand, dass Kronecker ein namhafter Mathematiker war, verlieh seinem Konflikt mit Cantor ein solches Gewicht. Und ihre Meinungsverschiedenheiten reichten tief - es waren solche der Grundüberzeugungen. Kronecker war zutiefst überzeugt davon, dass alles außer ganzen Zahlen unnatürlich sei. Den Umgang mit irrationalen Zahlen hielt er für widernatürlich. Und er warf Cantor vor, er sei ein «Jugendverderber», weil er solche Begriffe lehre."
[zitiert nach: Amir D. Aczel: Die Natur der Unendlichkeit; Mathematik, Kabbala und das Geheimnis des Aleph]

Man könnte fast sagen: der ganze Beweis hat nichts gebracht.)

Und überhaupt ist es pure Ideologie der Mathematik, dass es "die" (d.h. endgültige, einzig wahre) Mathematik gebe. Sie ist immer auch historisch und kulturabhängig.

Aber auch der Anlass ist bezeichnend: die irrationalen Zahlen sind nämlich tatsächlich irgendwie "irrational" im Sinne von "gehirnausrenkend": wie so oft in der Wissenschaft (z.B. auch in der Relativitäts- und Quantentheorie) reicht da der menschliche Verstand nicht, um seinen mathematischen Krücken zu folgen.

(Und das ist prinzipiell so bzw. allgemeinmenschlich, geht also nicht nur angeblich dummen SchülerInnen so.)

Nur muss das ja nicht unbedingt ein Nachteil sein, sondern macht es Wissenschaft vielleicht sogar aus: dass sie sich Instrumente (z.B. das Teleskop und Mikroskop) schafft, die weiter reichen als die menschliche Anschauung.

Hübsch schizophren macht es dennoch: z.B. "wissen" wir alle, dass die Erde eine Kugel ist, und "glauben"/leben dennoch im ganz normalen Alltag, dass sie flach wie eine Scheibe ist. Ja, die Kugelgestalt als Globus oder auf einem Foto aus dem Weltraum ist gerade so faszinierend, weil sie so atemberaubend fremd ist:

Immerhin hat Pythagoras noch gewusst, dass es mehr als nur Mathematik gibt (z.B. Religion oder [heute wohl zu Recht meistens ein Synonym für Weltflucht und Schwachsinn] "Esoterik").

Irrationalität wird üblicherweise als gefährliche Gefühlsduselei, also negativ verstanden. Man kann ihr aber durchaus auch positive Aspekte abgewinnen, wenn man sie wie Ernst Peter Fischer in seinem Buch

An den Grenzen des Denkens; Wolfgang Pauli - Ein Nobelpreisträger über die Nachtseiten der Wissenschaft; Herder spektrum

als Betrachtung des Einmaligen und nicht (experimentell) Wiederholbaren definiert:

„Was die Naturwissenschaften erfassen, wird gewöhnlich als »rational« bezeichnet. Ein allgemein gültiges Naturgesetz stellt einen rationalen - rational fassbaren - Aspekt der Natur dar. In dieser Sicht gehört das Einmalige nicht dazu, was im Umkehrschluss heißt, dass es irrational ist. Dies klingt zwar logisch und einfach genug, spricht aber so etwas wie eine Verurteilung aus, denn mit Irrationalität will niemand etwas zu tun haben - zumindest nicht in wissenschaftlichen Kreisen. Wer einmalige und nicht wiederholbare Ereignisse zum Gegenstand einer Untersuchung machen will, muss erst lernen, die Bedeutung des Irrationalen positiv zu verändern. »Irrational« sollte nämlich nichts mehr mit »unsinnig« oder »verrückt« zu tun haben. Als »irrational« sollte vielmehr das verstanden werden, für das sich kein allgemeines Gesetz formulieren lässt. Die Zufälle des Lebens gehören ganz sicher dazu - und damit jede individuelle Existenz. Die Welt steckt voller Irrationalitäten - das Schicksal eines jeden Einzelnen gehört dazu -, und es wäre ein weitreichender Mangel der Wissenschaft, wenn sie sich selbst verbietet, sich damit zu befassen.“

Rauchen kann tödlich sein

Warnhinweis: Der Beweis der Irrationalität der (und anderer irrationaler Zahlen) ist zu nichts zu gebrauchen, es gibt keinerlei außermathematische Anwendung. Und das ist aus ganz grundsätzlichen Gründen so: hat unendlich viele - und zudem unregelmäßige - Nachkommastellen, dass kein Computer damit umgehen kann und - etwa in Metern gemessen - die Zahlen weit hinterm Komma kleiner sind als jedes Atom (was allerdings auch schon bei 1/3 = 0,333333333... der Fall war). Mit dem üblicherweise in der 9. Klasse anstehenden Beweis der Irrationalität der nimmt die Mathematik also endgültig Abschied von jeder Anwendung, und man könnte fast sagen: wird sie überhaupt erst richtige Mathematik.

Zwei Ballonfahrer fahren nebeneinander im Nebel. Ruft der eine verzweifelt zum anderen rüber: "Wo sind wir?" Der andere denkt seelenruhig zwei Stunden nach und antwortet dann: "Im Ballon!"

Welchen Beruf hat der zweite?

Mathematiker!, denn die Antwort

• hat ewig lang auf sich warten lassen,
• ist absolut exakt und
• völlig unnütz!