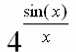-
Aufgabe:
Nenne jeweils ein alltägliches Beispiel (außer Schuhgrößen) für
-
eine Zuordnung, die keine Funktion ist,
-
eine Funktion, deren Umkehrung keine Funktion ist,
-
eine Funktion, deren Umkehrung auch eine Funktion ist.
Begründe jeweils kurz.
-
Aufgabe:
Die Mathematiker beschäftigen sich nicht mit allen Zuordnungen, sondern nur mit ganz speziellen. Welchen?
-
Aufgabe:
Zeichne
und begründe, weshalb (k)ein Funktionsgraph vorliegt.
-
Aufgabe:
Gegeben sei
f : y = 7x - 5
-
Was ist die Bezeichnung für f ?
-
Was ist die Bezeichnung für y = 7x - 5 ?
-
Was ist die Bezeichnung für 7x - 5 ?
-
Aufgabe:
-
Wie überprüft man, ob der Punkt P (3 | 8) auf dem Graphen von f : y = 7x - 5 liegt?
-
Vervollständige:
| Geometrie | Algebra |
| Ein Punkt P (x | y ) liegt genau dann auf dem Funktionsgraphen der Funktion f, | wenn ... |
-
Aufgabe:
Man kann eine Funktion auch als eine Art Maschine ansehen.
-
Welche x darf man in die Maschine y = x2 eingeben?
-
Welche x darf man in die Maschine y = 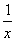 eingeben?
eingeben?
-
Welche x darf man in die Maschine y = 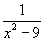 eingeben?
eingeben?
-
Was macht die Maschine y = 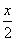 mit jedem x und was mit dem Spezialfall x = 17?
mit jedem x und was mit dem Spezialfall x = 17?
-
Was macht die Maschine y = 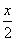 + 3 mit jedem x und was mit dem Spezialfall x = 17?
+ 3 mit jedem x und was mit dem Spezialfall x = 17?
-
Was macht die Maschine y = 3 mit jedem x und was mit dem Spezialfall x = 17?
-
Aufgabe:
Bei Funktionsgraphen interessieren
Nenne je ein Beispiel.
-
Aufgabe:
Gegeben sei die Funktion f: y = - 3 x5 + 19x3 -15. Wie kann der Funktionsgraph aussehen?
-
Aufgabe:
Beschreibe den folgenden Funktionsgraphen, indem Du
-
wie IMMER von links nach rechts gehst,
-
wichtige Punkte eindeutig markierst (z.B. x1, x2, x3 ...)
-
in einem zugehörigen Text die Details (Punkte, Intervalle) erklärst:
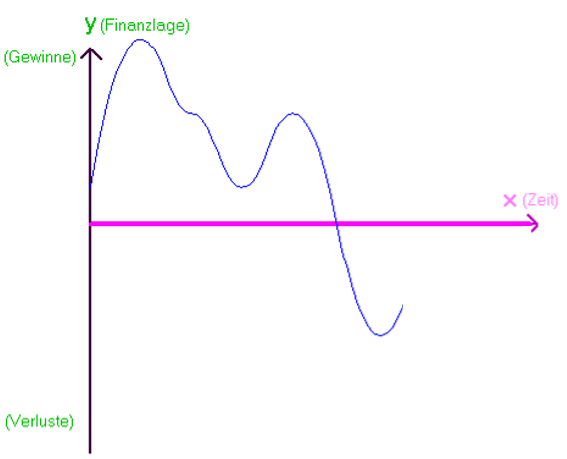
-
Aufgabe:
Beschreibe in einem Text mit anschaulichen und erklärten Graphiken die wichtigsten Eigenschaften der von Dir (in Deiner Gruppe) untersuchten speziellen Funktionen (keine Rechnungen!).
-
Aufgabe:
Gegeben sei die Funktion f : y = 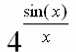
Zerlege die Funktion in Teilfunktionen und erarbeite daraus sinnvolle x-Werte für eine Wertetabelle (keine Rechnung!).

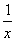 eingeben?
eingeben?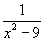 eingeben?
eingeben?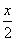 mit jedem x und was mit dem Spezialfall x = 17?
mit jedem x und was mit dem Spezialfall x = 17?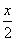 + 3 mit jedem x und was mit dem Spezialfall x = 17?
+ 3 mit jedem x und was mit dem Spezialfall x = 17?