Es beruht ja nicht (nur) auf Notwehr (Überarbeitung durch die hohe Stundenzahl und Korrekturen) und Denkfaulheit, wenn LehrerInnen immer dasselbe durchnehmen.

Sondern es gibt nicht nur Themen, sondern auch spezielle Aufgaben, die nun mal besonders geeignet für den Unterricht sind, und solch ein Fundus besonders geeigneter Aufgaben macht ja eben gerade auch die erfahrene Lehrkraft aus.

(Als Jungkollege, der ja "sowieso" alles anders machen will

[also nicht einer von jenen Langeweilern, die schon mit 25 Jahren das gegebene Programm "dufte" finden und eh alles nachbeten, also noch nie eine eigene Meinung hatten],

braucht man so seine Zeit, um wiederzuentdecken, was besonders geeignet ist:

z.B. "Der Erlkönig" von Goethe:

• da ist nicht nur [deshalb nimmt man ja in der frühen Mittelstufe so gerne Balladen durch] "action" drin;

• das ist nicht nur mit der "Angst vorm schwarzen Mann" und ein wenig gruseligem Horror jugendnah,

• sondern das ist auch höchst raffiniert geschrieben, indem offen bleibt, ob es den Erlkönig gibt oder nicht,

• und da lässt sich auch die halbe Stilistik motivierend einführen.)

Dementsprechend gibt es natürlich auch Mathematikaufgaben, die besonders für den Unterricht geeignet sind - und solche, die es nicht sind.

Kriterien sind da z.B.

• Anschaulichkeit,

• leichte Rechenbarkeit,

• dass ein mathematischer Sachverhalt exemplarisch besonders schön und offensichtlich eingeführt wird,

• einfache Anwendbarkeit auf Außermathematisches

• ...

Es kommt aber eben auch darauf an, wie man eine Aufgabe stellt.

Es scheint mir zwei Gründe zu geben, weshalb man diese ja in der Tat nicht ganz einfache Aufgabe stellt:

1. "einfach" nur, weil die Aufgabe so schwierig ist?
   (da kann man unter der neudeutsch Schüler-"Klientel" so hübsch die Spreu vom Weizen trennen)

2. weil das ein ästhetisches Problem ist!?
   (nicht zu verwechseln mit irgendeiner "Anwendung": wann denn liegt o.g. Problem mal in der "Wirklichkeit" an?!)

Damit aber zu der Frage, wie man diese Aufgabe am besten stellt:

Bei dieser nicht ganz einfachen Aufgabe helfen Schulbücher üblicherweise immerhin mit einer Abbildung, also z.B.

Solch eine (zweidimensionale) Abbildung hat schon - je nachdem - entscheidende Vor- und Nachteile:

• es wird schon der entscheidende Tipp gegeben bzw. es wird suggeriert, dass die Lösungsschritte im Zweidimensionalen stattfinden

(Kugel → Kreis, Kegel → Dreieck; "Pythagoras, ick hör dir trapsen"),

wobei das Kegelvolumen natürlich dreidimensional bleibt; man könnte sowas "schülerfreundlich" nennen;

• in der Abbildung liegt schon (auch wieder "schülerfreundlich") annähernd der eigentlich doch erst gesuchte Kegel mit maximalem Volumen vor (wodurch nebenbei schwierige Fallunterscheidungen [Kegelhöhe größer oder kleiner als Kugelradius] ausgeschlossen werden).

Man könnte - jetzt negativ gewendet - also sagen: vor lauter Schülerfreundlichkeit ist die Luft aus der Aufgabe raus, es gibt gar keinen Grund mehr, nach dem Kegel mit maximalem Volumen zu suchen.

Was aber vor allem schon raus ist, ist die Schönheit des Problems:

1. einfach die Schönheit der Kugel: vgl. , also ein Buch, in dem sich der Autor Max Goldt auf seine typische Art liebevoll lustig über die kugelförmige "Kunst im öffentlichen Raum" fast aller Fußgängerzonen macht;

2. ganz offensichtlich eine analoge Schönheit von Kegeln.

Selbst die so vermeintlich knochentrockenen Mathematiker sind ja abgrundtief fasziniert von Kegeln.

Und ich glaube ja noch immer, dass sich Schönheit manchmal halbwegs erklären lässt: Kugel und Kegel haben eine mathematisch beschreibbare Perfektion, die gerade in ihrer frappierenden Einfachheit begründet ist.

(Nebenbei: ist eigentlich schon mal jemandem aufgefallen, dass sich "Kugel" und "Kegel" - bis auf einen einzigen Buchstaben - sehr ähnlich anhören und das vielleicht seinen Grund hat?)

3. ist auch das Problem der "Einschreibung" eines Kegels in eine Kugel schön:

1. dass das überhaupt immer passt;

2. welche Kegel da überhaupt möglich sind: die Kugel ist das "Gefängnis" aller möglichen Kegel, und dennoch gibt es unendlich viele mögliche Kegel;

3. dass die möglichen Kegel ganz offensichtlich verschiedene Volumina haben und bei zunehmender Höhe das Volumen erst zu- und dann wieder abnimmt, so dass ganz offensichtlich "irgendwo dazwischen" ein Maximum angenommen wird;

4. womit sich dann überhaupt erst die Frage aufkommt, wo genau (bei welchem der unendlich vielen möglichen Kegel) das der Fall ist.

All diese Punkte sind aber schon tot, wenn

• man von vornherein nach dem (dann offensichtlich vorhandenen) Maximum fragt,

• es mit der Abbildung sogar schon annähernd zeigt,

• ein Buch (notgedrungen) ein statisches Abbild gibt.

Am besten lässt man die SchülerInnen das Problem natürlich handgreiflich basteln, damit sie wissen, was sie tun (!).

Allerdings muss man natürlich auch die Grenzen solcher "Handgreiflichkeit" sehen: es ist aus offensichtlichen technischen Gründen im Unterricht ganz ungeheuer schwierig bis geradezu unmöglich, die "Einschreibung" von Kegeln (insbesondere im Plural) in eine Kugel zu bewerkstelligen.

(Und schon gar nicht ist handwerklich der kontinuierliche Durchlauf aller möglichen Kegel [s.u.] machbar.)

Hier wäre nun also mal wirklich eine Computeranimation angesagt:

(Besser wäre natürlich noch ein kontinuierlicher "Durchlauf" der möglichen Kegel; ich habe aber weder Zeit noch Lust, das jetzt zu programmieren;
es wäre aber eine schöne Aufgabe für SchülerInnen mit Programmierkenntnissen, das zu programmieren [warum soll die Lehrkraft alles selbst tun?], denn bei der Programmierung würden sie schon eine Menge mathematisches Rüstzeug für den Lösungsweg der Aufgabe lernen;

man mache sich zudem nichts vor: jedes Modell suggeriert schon etwas:

• z.B. ist jede Computeranimation natürlich auch schon wieder zweidimensional;

• und natürlich schreit die Animation nach der Frage, wann [als Standbild] der Kegel mit größtem Volumen vorliegt: aber die Frage ergibt sich "aus der Sache heraus" und muss deshalb nicht mal mehr explizit gestellt werden.)

Solch eine Animation hat nun zwei Vorteile:

1. ergibt sich die Frage nach dem Kegel mit maximalem Volumen von selbst, bzw. sie drängt sich beim erst breiter und dann wieder schmaler werdenden Kegel automatisch auf;

2. anhand solch einer Animation sieht man schnell

(entdeckt es aber selbst, statt es wie in Büchern vorgegeben zu bekommen),

dass das Volumenmaximum etwa bei liegt (und liegen muss!), wenn also die Kegelhöhe h etwa das 3/2-fache des Kugelradius R ist.

Hier also haben wir nun tatsächlich ein schönes Beispiel für "erst denken, dann (gar nicht mehr) rechnen": man hat vor aller Rechnung schon einen "Maßstab" für die Größenordnung der Lösung - und kann daran später auch potentiell falsche Lösungen messen, die einem dann überhaupt erst auffallen.

Man könnte des weiteren durch reine Überlegung herausfinden, weshalb das Volumenmaximum bei etwa 3/2 R liegen muss:

• mit zunehmender Kegelhöhe h nimmt der Kegelradius r erst (bis zur Mitte) zu und dann wieder ab;

• es scheint also auf den ersten Blick Symmetrie bzgl. der Kugelhälfte vorzuliegen;

• nun liegt allerdings die Kegelspitze oben und sein "dickes Ende" unten, d.h. ein Großteil des Volumens kommt in der unteren Kegelhälfte zustande.

Wohlgemerkt: das 3/2-fache ist nur ein "Maßstab", und es stört dann nicht, wenn (nach der Rechnung) als exaktes Ergebnis h = 4/3 ● R herauskommt.

(siehe zur exakten Rechnung ;

das aber ist bei Behandlung [nicht nur] dieser Aufgabe auch zu vermitteln: ein "andächtiges" Staunen [!!!] darüber, dass nach ellenlanger, durchaus schwieriger bzw. zumindest umständlicher Rechnung der höchst einfache Wert h = 4/3 ● R herauskommt; und dann wäre es ein interessantes Unterfangen, die Rechnung zurück zu verfolgen und herauszufinden, wo dieser einfache Wert zustande kam; vgl. "den Ergebnissen nachgehen [statt sie nur zu akzeptieren"].)

Es sei noch mal auf die "Schülerfreundlichkeit" zurück gekommen:

• ein ganz besonders "freundliches" Schulbuch gibt noch entscheidende (zu viele!) Tipps durch Hilfslinien:

Hier nun also ist der Tipp "Dreieck" meterdick klar: fehlt nur noch der rechte Winkel zwischen h und r, und schon hört man auch den "Satz des Pythagoras" bzw. die pythagoräische Satzgruppe raus (nach der ja auch in der o.g. Lösung gearbeitet wird);

• ein anderes Buch ist schon ein bisschen "gemeiner", wenn es den rechten Winkel zwischen h und r gezielt verschweigt

(die SchülerInnen die zweidimensionale Projektion und das Dreieck also überhaupt erst selbst entdecken müssen):

• so richtig hundsgemein (und dafür habe ich kein Verständnis mehr) wirds, wenn (wie tatsächlich in einem Schulbuch geschehen) als Tipp gegeben wird, das Kugelvolumen abhängig vom Kegel-Öffnungswinkel α zu berechnen:

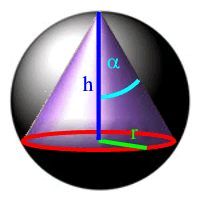
Damit nämlich kommt unweigerlich der Tangens herein, dessen Ableitung die SchülerInnen zum Zeitpunkt, an dem diese Aufgabe üblicher- und sinnvollerweise gestellt wird (Ableitung ganzrationaler Funktionen), noch gar nicht kennen.

Aber selbst das ist mir Anlass für "erst denken, dann (gar nicht mehr) rechnen":

• weil man den Tangens noch gar nicht ableiten kann,

• muss der Tangens zweimal (noch in einem anderen Dreieck) angewandt werden, damit er letztlich wieder rausfliegt.
  Womit der Tipp im Raum steht: suche ein weiteres Dreieck, in dem ebenfalls α vorkommt und der Tangens angewandt werden kann!

Nebenbei: die zweimalige Anwendung des Tangens führt auch zum Höhensatz (s. die Lösung oben). Warum also nicht gleich?

Nun scheinen mir aber die beiden Zugänge über den

1. Höhensatz und

2. Öffnungswinkel α

gleichermaßen ungünstig, weil

1. "um die Ecke gedacht" und also

2. schülerfremd.

Denn beide bauen auf dem Hilfsdreieck unterhalb des Kegels auf:

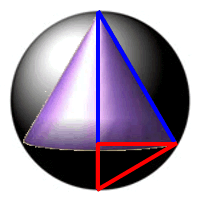
1. Der Höhensatz wird auf das Gesamtdreieck angewandt,

2. Im Hilfsdreieck ergibt sich rechts der zweite Winkel α und lässt sich deshalb nochmals der Tangens anwenden.

Nur liegt dieses Hilfsdreieck weit außerhalb aller intuitiven Betrachtung, ja der Kegel wird - dreidimensional gesehen - zu einem Doppelkegel (ausnahmsweise nicht mit sich berührenden Spitzen, sondern Basen) ergänzt.

Nun bleibt die nachfolgende Rechnung zwar immer abstrakt, aber es gibt doch einen intuitiveren Zugang:

die überhaupt möglichen Kegel ergeben sich ja gerade durch das "Gefängnis" der Kugel, und diese ist definiert durch ihren Radius R. Dieser Radius R ist sozusagen der "Leitstrahl", der die Basis des Kegels "führt":

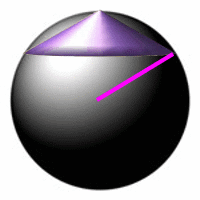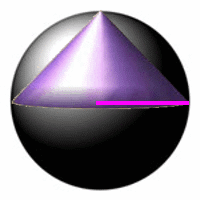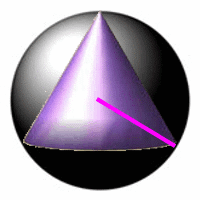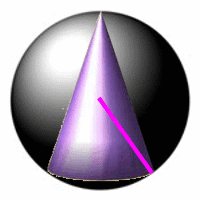
Wenn man aber den Kugelradius R derart in den Kegel einzeichnet, ergibt sich folgendes Dreieck, das man - mit demselben Ergebnis wie bei der Tangens- und Höhensatzanwendung - sehr leicht mit dem Satz des Pythagoras behandeln kann

(um einen Zusammenhang zwischen Kegelradius r, Kegelhöhe h und dem Kugelradius R heraus zu finden, also eine gegenseitige Abhängigkeit von r und h zu erhalten und somit eine einzige Variable zu erhalten):

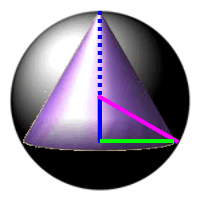
Der Vorteil des "Leitstrahls" ist aber, dass diese Hilfslinie

1. konstruktiv nahe liegt (die möglichen Kegel überhaupt erst definiert),

2. im Kegel liegt

3. und als "Abfallprodukt" zu einer erheblich einfacheren Rechnung führt
   (den Satz des Pythagoras beherrscht doch hoffentlich noch jeder, aber wer kennt nach langer Zeit noch den Höhensatz - und erkennt seine Anwendbarkeit?).

All das schließt ja nicht aus, dass SchülerInnen von sich aus dennoch andere Wege (eben z.B. über den Höhensatz oder den Tangens) gehen.

Ich höre schon einen entscheidenden Einwand: mein Kugel-/Kegel-Vorschlag sei zwar sehr (zu?) schön, aber in der Schule "leider, leider" kaum machbar: man brauche für diese Kugel-/Kegelaufgabe viel zu viel Zeit, die

1. beim nun mal vorhandenen Stoffdruck einfach nicht vorhanden,

2. aber auch gar nicht verantwortbar sei, weil die Kugel-/Kegelaufgabe doch nur ein Beispiel für viel Wichtigeres, nämlich Minimaxprobleme, sei und die SchülerInnen ja gerade lernen müssten, möglichst unterschiedliche Minimaxprobleme zu lösen
   (u.a., um die vielfältige Anwendbarkeit der Minimaxrechnung zu erkennen).

Da antworte ich schlicht:

1. ich bin durchaus Realist und sehe die Grenzen, ja fast schon die Unmöglichkeit solch größerer "Projekte" im gnadenlos vorstrukturierten Schulalltag (vgl. "Stoffbegrenzung tut not");

2. dass die Kugel-/Kegel-Aufgabe nur ein Beispiel für anderes, also letztlich nur Vorwand ist, ist doch immerhin mal ebenso entwaffnend wie bezeichnend ehrlich;

3. ich glaube dennoch, dass solche Unterrichts-Exkurse, wie ich hier einen vorgeführt habe, zumindest ab und zu möglich und sogar nötig sind. Ohne solche Exkurse kommt nie (im vorliegenden Fall durchaus innermathematisches) "Fleisch an die Knochen".