der schönste Beweis aller Zeiten
B) Vorgeschichte und Hintergründe des Beweises
c) eine merkwürdige Strecke
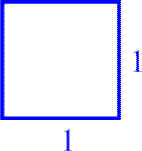
Angenommen, ein Tisch hat die einfachste Form und die einfachsten Maße, die überhaupt nur denkbar sind:
er ist quadratisch und
hat die Seitenlänge ein Meter:

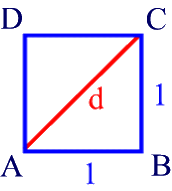
Da liegt doch immerhin die Frage sehr nah, wie lang die wiederum denkbar einfachste Strecke in diesem Quadrat, nämlich die Diagonale d ist:
Damit man sich nicht vertue:
mag ja sein, dass es solche quadratischen Tische gibt, und viele werden der Einfachheit halber auch die Seitenlänge 1 m haben;
aber die Frage nach der Länge der Diagonalen ist zweifelsohne nur von theoretischem Interesse, denn was interessiert´s mich schon, wie lang mein Tisch "querdrüber" ist?
Nun, auch dazu lässt sich natürlich ein "Anwendungsproblem" herbeimogeln: wenn ich nämlich eine runde Tischdecke kaufen will, die exakt auf den Tisch passt (seinen Umkreis bildet):

Offensichtlich muss der Durchmesser der runden Decke genau gleich der Diagonalenlänge des Quadrats sein.
Aber ich mag keine Tischdecken, ich finde sie kitschig und naturbelassene Tische viel schöner! Außerdem würde einen jetzt jede gute Hausfrau darüber aufklären, dass man Tischdecken niemals genau passend kauft, sondern sie [z.B. gegen eventuelles Verrutschen] immer ein wenig überlappen lässt. Wogegen man immerhin einwenden könnte: um die Tischdecke überlappend zu kaufen, muss ich immerhin doch wissen, was passend wäre (der Durchmesser der überlappenden runden Decke muss größer oder gleich der Diagonalenlänge des Quadrats sein).
Immerhin ist die Diagonale oft
praktisch, weil sie die kürzeste Verbindung (von A nach C) ist;
von ästhetischem Interesse:
sie passt halt so hübsch quer ins Quadrat rein wie sonst keine andere Strecke (außer natürlich der zweiten Diagonalen);
in der Kunst und im Film sind Diagonalen immer wieder wichtig, weil sie Übersichtlichkeit oder auch Dramatik (Bewegung) erzeugen

("Apollo und Daphne" von Bernini)
bzw. soziale Rangfolgen zeigen:

(Elizabeth Taylor & James Dean im Film "Giganten")
Damit aber zurück zur Frage, wie lang die Diagonale d in dem Quadrat ist:
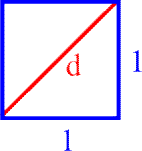
Es liegt doch wohl die Vermutung nahe:
wenn die Fläche so einfach ist (quadratisch),
wenn ihre Seitenlänge so einfach ist (1 m) und
wenn sich die Diagonale so einfach ergibt,
dann wird doch wohl auch die Diagonalenlänge sehr einfach sein!?
|
Stelle eine Vermutung auf, wie lang die Diagonale ist. | |
|
Zeichne ein Quadrat der Seitenlänge 1 dm und miss seine Diagonale! | |
|
Versuche, die Diagonalenlänge zu BERECHNEN! Notiere dabei alles, was Dir über das Quadrat bekannt ist. |
| Leider ist die Länge der scheinbar so einfachen Diagonale d nicht mit den uns zur Verfügung stehenden Mitteln berechenbar. |
Deshalb soll im folgenden ein kleiner Umweg gegangen werden. Wir werden sehen, dass er dennoch halbwegs zum Ziel führt (allerdings einem sehr merkwürdigen).
|
Dass MathematikerInnen diesen Umweg gegangen sind, ist wohl nur dadurch zu erklären, dass sie (wie so oft) vorerst auch nicht weiter gewusst und deshalb erstmal "rumgeknobelt" haben. |
|
In

und also auch in

ist also
| d = |