Problem- statt Lösungsmathematik

Dennoch wird mir aber im "klassischen" Mathematikunterricht viel zu sehr von den (vorausgesetzten) Lösungen ausgegangen:

1. werden fast nur (mit den gerade zur Verfügung stehenden Mitteln) lösbare Aufgaben durchgenommen, bzw. Unlösbarkeit taucht nur sehr selten und dann eher "pro forma" auf;
2. sind die allermeisten Aufgaben (u.a. auch "eingekleideten" Anwendungsaufgaben) von der Lösung aus gedacht;
3. tauchen in Klausuren fast nur lösbare Aufgaben auf, weil diese hübsch einfach nach der Wahr-/Falsch-Logik bewertbar sind
   (fast die einzigen Ausnahmen sind solche quadratische Gleichungen, bei deren Lösungsversuch sich eine negative Diskriminante ergibt).

(Un-)Lösbarkeit erscheint im normalen Mathematikunterricht immer nur als subjektiv-individuelle Eigenschaft (Dummheit oder Klugheit desjenigen, der einen Lösungsversuch startet): Wenn SchülerInnen bei Aufgaben keine Lösungen erhalten, wissen sie immerhin ganz genau: "Ich habe versagt."

Wenn aber alles lösbar ist bzw. schon längst gelöst worden ist, ist "die Luft raus": es gibt kein Problem mehr (außer der individuellen Meisterung) und somit auch weder eine Herausforderung noch Neugierde.

Kommt hinzu, dass mit der vorausgesetzten Lösbarkeit ein höchst einseitiges Bild der Welt geliefert wird bzw. entsteht:

1. kann die Mathematik nur über einen sehr kleinen, wenn auch durchaus wichtigen Teil der Welt Lösungen (!) anbieten (dafür aber durchaus erstaunliche),
2. ist die Lösbarkeit ja nicht mal innermathematisch permanente Regel, sei´s, dass Aufgaben
   1. prinzipiell nicht lösbar sind
      (bzw. laut Gödel nicht entscheidbar ist, ob sie lösbar sind),
   2. noch nicht gelöst werden können
      (mit den derzeitigen Schülermitteln, aber evtl. auch noch nicht von der vordersten Forscheravantgarde
      [vgl. etwa das "Dreikörperproblem" oder die "Goldbachsche Vermutung"]).

Ich hielte es also durchaus mal für ein interessantes Thema, sich im Unterricht phasenweise ausschließlich mit Unlösbarkeit (und d.h. eben auch: den Grenzen mathematischer Aussagekraft) bzw. dem langen Weg zur Lösbarkeit zu beschäftigen, und ich bin fest davon überzeugt, dass man dabei mindestens so viel über Mathematik lernen kann wie aus gelösten Problemen

(u.a. eben, weil auch an [lange Zeit] ungelösten Problemen typische mathematische Denkweisen klar werden, beim Lösungsversuch oftmals aber auch viele interessante anderweitige Lösungen abfielen;
und das ist - wie etwa Singh zeigt - selbst dann auch für SchülerInnen erhellend, wenn die eigentlichen Probleme erheblich zu schwierig für die Schule sind):

	Simon Singh: Fermats letzter Satz; Die abenteuerliche Geschichte eines mathematischen Rätsels; dtv
	Apostolos Doxiadis: Onkel Petros und die Goldbachsche Vermutung; Lübbe
	Heinrich Tietze: Gelöste und ungelöste mathematische Probleme; C.H. Beck (leider vergriffen; besonders spannend ist insbesondere, dass einige der in diesem Buch noch als ungelöst aufgeführten Probleme inzwischen gelöst wurden)

Das "statt" in "Problem- statt Lösungsmathematik" war natürlich nur provokativ, nicht wirklich ausschließlich gemeint: allzu viele unlösbare oder auch für SchülerInnen noch nicht lösbare Aufgaben können selbstverständlich extrem frustrierend sein, und in der Regel sollte nach einem Problem auch das Glücksgefühl eines "Heureka" folgen bzw. deutlich werden, dass die Mathematik erstaunlich viele Probleme lösen kann.

Außerdem werden - wie schon oben angedeutet - im Schulunterricht fast immer nur Aufgaben angegangen, die zum derzeitig anliegenden Stoff passen. Das hat durchaus seine Vorteile

(denn es muss ja seine guten Gründe haben, dass sich der derzeit gängige Unterricht ergeben hat):

• es werden nur Aufgaben behandelt, die in eine Sachlogik passen, die sich seit langem bewährt hat;
• der Übergang vom Problem zum mathematischen Stoff ist sehr leicht und daher (angesichts des allgegenwärtigen Stoffdrucks) wenig zeitraubend;
• der Unterricht ist verlässlich, denn die SchülerInnen wissen immer, wo sie "dran" sind: wenn gerade die eine Schwierigkeit (z.B. ganzrationale Funktionen) anliegt, werden sie nicht durch andere Schwierigkeiten (z.B. Wurzeln) abgelenkt - und auch nicht an altem Stoff gemessen.

Aber selbstverständlich sind SchülerInnen nach solch mathematisch enggeführtem Unterricht in der Regel (wie etwa in TIMSS oder PISA) nicht in der Lage, Aufgaben zu lösen,

• bei denen die zur Lösung notwendigen mathematischen Verfahren nicht direkt am Weg liegen
• oder für deren Lösung es "nur" gesunder Anschauung, nicht aber eines eindeutigen Rechenverfahrens bedarf.

Hier helfen auch nicht allein (noch so gute) Anwendungsaufgaben, solange sie doch wieder nur passend zum derzeit anliegenden Stoff gedacht werden

(und die SchülerInnen immer schon von vornherein wissen: "es wird schon [derzeit passende] Mathematik dabei rauskommen, ist also letztlich doch nur Vorwand").

Sondern es müssten (nach Abbau des Stoffdrucks!) wirklich gänzlich offene Aufgaben angegangen werden - oder zumindest doch welche, die nicht eindeutig auf Lösungen hin gedacht sind:

• Aufgaben, die nicht allein mit Mathematik lösbar sind bzw. an denen die Mathematik auf Anhieb gar nicht erkennbar ist
  (vgl. etwa das Beispiel in "Mathematik und Psychologie");
• echte "Orientierungsaufgaben", und sei´s wortwörtlich zur ;

Sinnvoll wären insbesondere Problemaufgaben, in denen ein wortwörtlicher Handlungsauftrag vorläge, zu dessen Erledigung Mathematik notwendig bzw. hilfreich ist:

• miss Dinge aus!
• erkläre oder konstruiere technische Geräte!
  • Wenn man bei der "flinken Flasche" von UHU den gelben Deckel abnimmt, erscheint ein schwarzes Röhrchen, aus dem der Kleber heraus fließt. Um nun nicht (mit dem schwarzen Röhrchen) eine dünne, sondern eine dicke Klebespur zu erhalten, kann man das mit dem Pfeil versehene gelbe Teil drehen, worauf sich ein weiteres gelbes Teil nach oben schiebt.

Aufgabe: Denke Dir einen Mechanismus aus, der dieses bewirkt - und schaue erst nachher

(durch Auseinandernehmen der "restentleerten" Flasche)

nach, wie die Ingenieure das Problem bei der UHU-Flasche gelöst haben!

• Wie kann man ein Kilometerzähler konstruieren?
  (d.h. nicht nachschauen, sondern selbst auf die Idee kommen, wie sich nach neun Ziffern des ersten Rädchens das zweite um eine Ziffer weiter bewegt;
  wobei man man eine Menge über das Zehnersystem lernt - sowie in simpler Übertragung auch über andere Zahlensysteme;
  vgl. )

• Die astronomische Uhr im Dom zu Münster

(vgl. )

ist (obwohl uralt) ein hochkomplexes feinmechanisches Meisterwerk. Fangen wir also mit dem offensichtlichsten und einfachsten Effekt an:

Mittags bimmeln und tuten die Figuren oben ganz rechts und ganz links die Uhrzeit, und dann

• geht oben im rot markierten Bereich rechts ein Türchen auf,

• treten nacheinander fünf Figuren, darunter die Dreikönige, heraus,

• laufen sie von rechts nach links auf dem runden Balkon,

• wenden sich die Dreikönige, sobald sie vor der Gottesmutter mit Kind (genau in der Mitte) sind, diesen zu,

• verneigen sie sich,

• wenden sie sich wieder ab

• und verschwinden in der Tür links.

All diese Figurenbewegungen sind gut sichtbar - nicht aber der Mechanismus, der all diese Bewegungen bewirkt.

Und ich möchte ergänzen, dass dieser Mechanismus glücklicherweise nicht direkt einsehbar ist - und auch kein "Uhrenwärter" erreichbar ist, der ihn einem zeigen oder auch nur erklären, also alles voreilig verraten könnte.

Aufgabe: entwickle selbst einen (klapprigen) Mechanismus, der die o.g. Bewegungen ausführt! Du hast zehn Unterrichtsstunden Zeit.

(... eine Aufgabe, die so einiges geometrisches [und mechanisches?] Verständnis voraussetzt - oder erzeugt?!, und zwar ohne jemals explizit "mathematisch" zu werden.)

• oder schlichtweg eine Mathematik, die aus der "Sachkunde" (früher sehr schön: Heimatkunde) hervorgeht.

• was unterscheidet Mondphasen von Mondfinsternissen (vgl. ) - und wann treten sie auf (physikalische Gründe, Intervalle)?
  (Arbeitsanweisung: beobachte den Mond, statt nur einfach Bücher über den Mond zu lesen!)
• baue ein Modell für den Kathetensatz (vgl. )!
  (der immense Vorteil dabei ist, dass sich da die mathematische Forderung aus den technischen Anforderungen ergibt);
• schreibe ein Programm, das Berühr- und Sattelpunkte ganzrationaler Funktionen dritten Grades verdeutlicht!:

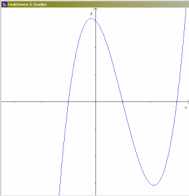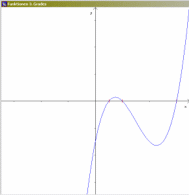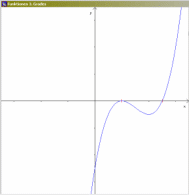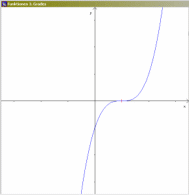
vgl.

Die SchülerInnen müssen einfach viel mehr haptisch tun

(und die "eigentliche" Mathematik, die - wie erstaunlich! - rein im Kopf erfolgt, kann noch immer folgen).

Und wir LehrerInnen werden wieder über die Buntheit der Wirklichkeit (und die vielfältigen Anwendungsmöglichkeiten von Mathematik) staunen lernen müssen: wir behaupten ja meist nur, dass die Mathematik allüberall anwendbar ist, wissen es

(konkrete Beispiele und ihre mathematischen Funktionsweisen; also z.B. die Statik einer parabelförmigen Brücke; vgl. )

aber auch nicht so genau.

Die Probleme können allerdings (und sollten ab und zu) durchaus auch innermathematisch sein, Hauptsache, sie werden veranschaulicht.

Solch ein innermathematisches Problem wäre beispielsweise die Frage: "Welche Basen und Koeffizienten sind bei Potenzen sinnvoll bzw. möglich und wie muss mit ihnen gerechnet werden (statt dass man die Potenzgesetze einfach nur fertig »vorsetzt«)?"

Da kämen dann - durchaus auch schon in einer 10. Klasse - solche Fragen auf wie "welche Definitionen sind wünschenswert (praktisch, in sich stimmig) - und welche nötig (d.h. was kann man als Satz folgern)?".